
- 大数据分析有用的资源
- 大数据分析 - 快速指南
- 大数据分析 - 资源
- 大数据分析 - 讨论
大数据分析-统计方法
分析数据时,可以采用统计方法。执行基本分析所需的基本工具是 -
- 相关性分析
- 方差分析
- 假设检验
当处理大型数据集时,它不会涉及问题,因为除了相关性分析之外,这些方法的计算量并不大。在这种情况下,总是可以取样并且结果应该是稳健的。
相关性分析
相关分析旨在寻找数值变量之间的线性关系。这可以在不同的情况下使用。一种常见的用途是探索性数据分析,本书的第 16.0.2 节中有一个这种方法的基本示例。首先,上述示例中使用的相关性度量基于皮尔逊系数。然而,还有另一个有趣的相关性指标,它不受异常值的影响。该指标称为斯皮尔曼相关性。
斯皮尔曼相关度量对于异常值的存在比皮尔逊方法更稳健,并且当数据不呈正态分布时,可以更好地估计数值变量之间的线性关系。
library(ggplot2)
# Select variables that are interesting to compare pearson and spearman
correlation methods.
x = diamonds[, c('x', 'y', 'z', 'price')]
# From the histograms we can expect differences in the correlations of both
metrics.
# In this case as the variables are clearly not normally distributed, the
spearman correlation
# is a better estimate of the linear relation among numeric variables.
par(mfrow = c(2,2))
colnm = names(x)
for(i in 1:4) {
hist(x[[i]], col = 'deepskyblue3', main = sprintf('Histogram of %s', colnm[i]))
}
par(mfrow = c(1,1))
从下图中的直方图中,我们可以预期两个指标的相关性存在差异。在这种情况下,由于变量显然不呈正态分布,因此斯皮尔曼相关性可以更好地估计数值变量之间的线性关系。
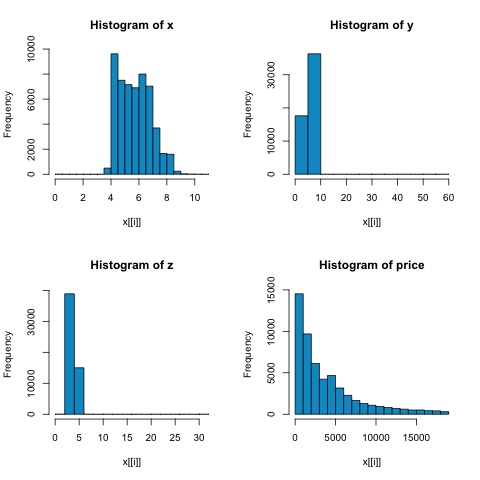
为了计算 R 中的相关性,请打开包含此代码部分的文件bda/part2/statistical_methods/correlation/correlation.R 。
## Correlation Matrix - Pearson and spearman cor_pearson <- cor(x, method = 'pearson') cor_spearman <- cor(x, method = 'spearman') ### Pearson Correlation print(cor_pearson) # x y z price # x 1.0000000 0.9747015 0.9707718 0.8844352 # y 0.9747015 1.0000000 0.9520057 0.8654209 # z 0.9707718 0.9520057 1.0000000 0.8612494 # price 0.8844352 0.8654209 0.8612494 1.0000000 ### Spearman Correlation print(cor_spearman) # x y z price # x 1.0000000 0.9978949 0.9873553 0.9631961 # y 0.9978949 1.0000000 0.9870675 0.9627188 # z 0.9873553 0.9870675 1.0000000 0.9572323 # price 0.9631961 0.9627188 0.9572323 1.0000000
卡方检验
卡方检验允许我们检验两个随机变量是否独立。这意味着每个变量的概率分布不会影响另一个变量。为了评估 R 中的测试,我们首先需要创建一个列联表,然后将该表传递给chisq.test R函数。
例如,让我们检查变量之间是否存在关联:钻石数据集中的切工和颜色。该测试的正式定义为 -
- H0:可变切割和钻石是独立的
- H1:可变切工和钻石不是独立的
我们会假设这两个变量之间存在关系,但测试可以给出一个客观的“规则”,说明这个结果的显着性或不显着性。
在下面的代码片段中,我们发现测试的 p 值为 2.2e-16,这实际上几乎为零。然后,在运行蒙特卡罗模拟测试后,我们发现 p 值为 0.0004998,仍然远低于阈值 0.05。这个结果意味着我们拒绝原假设 (H0),因此我们认为变量剪裁和颜色不是独立的。
library(ggplot2) # Use the table function to compute the contingency table tbl = table(diamonds$cut, diamonds$color) tbl # D E F G H I J # Fair 163 224 312 314 303 175 119 # Good 662 933 909 871 702 522 307 # Very Good 1513 2400 2164 2299 1824 1204 678 # Premium 1603 2337 2331 2924 2360 1428 808 # Ideal 2834 3903 3826 4884 3115 2093 896 # In order to run the test we just use the chisq.test function. chisq.test(tbl) # Pearson’s Chi-squared test # data: tbl # X-squared = 310.32, df = 24, p-value < 2.2e-16 # It is also possible to compute the p-values using a monte-carlo simulation # It's needed to add the simulate.p.value = TRUE flag and the amount of simulations chisq.test(tbl, simulate.p.value = TRUE, B = 2000) # Pearson’s Chi-squared test with simulated p-value (based on 2000 replicates) # data: tbl # X-squared = 310.32, df = NA, p-value = 0.0004998
T检验
t 检验的想法是评估标称变量的不同组之间数值变量的分布是否存在差异。为了证明这一点,我将选择因子变量切割的公平水平和理想水平,然后我们将比较这两组之间的数值变量的值。
data = diamonds[diamonds$cut %in% c('Fair', 'Ideal'), ]
data$cut = droplevels.factor(data$cut) # Drop levels that aren’t used from the
cut variable
df1 = data[, c('cut', 'price')]
# We can see the price means are different for each group
tapply(df1$price, df1$cut, mean)
# Fair Ideal
# 4358.758 3457.542
t 检验在 R 中通过t.test函数实现。t.test 的公式接口是最简单的使用方法,其思想是数字变量由组变量解释。
例如:t.test(numeric_variable ~ group_variable, data = data)。在前面的示例中,numeric_variable是price,group_variable是cut。
从统计角度来看,我们正在测试两组之间数值变量的分布是否存在差异。正式地,假设检验用原假设 (H0) 和备择假设 (H1) 来描述。
H0:公平组和理想组之间价格变量的分布没有差异
H1 公平群体和理想群体之间价格变量的分布存在差异
可以使用以下代码在 R 中实现以下内容 -
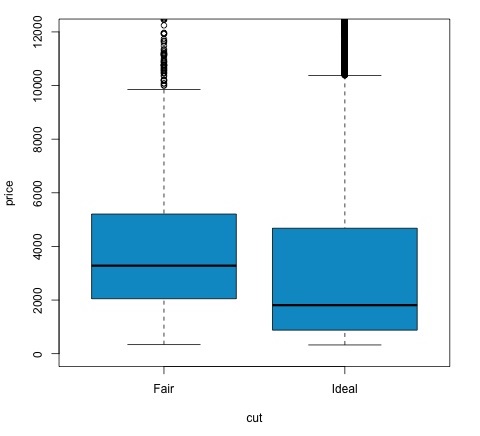
t.test(price ~ cut, data = data) # Welch Two Sample t-test # # data: price by cut # t = 9.7484, df = 1894.8, p-value < 2.2e-16 # alternative hypothesis: true difference in means is not equal to 0 # 95 percent confidence interval: # 719.9065 1082.5251 # sample estimates: # mean in group Fair mean in group Ideal # 4358.758 3457.542 # Another way to validate the previous results is to just plot the distributions using a box-plot plot(price ~ cut, data = data, ylim = c(0,12000), col = 'deepskyblue3')
我们可以通过检查 p 值是否低于 0.05 来分析测试结果。如果是这种情况,我们保留备择假设。这意味着我们发现了两个削减因子水平之间的价格差异。根据级别的名称,我们预计会出现此结果,但我们不会预计失败组中的平均价格会高于理想组中的平均价格。我们可以通过比较每个因素的平均值来看到这一点。
绘图命令生成一个图表,显示价格和切割变量之间的关系。这是一个箱线图;我们在第 16.0.1 节中介绍了该图,但它基本上显示了我们正在分析的两个削减水平的价格变量的分布。
方差分析
方差分析(ANOVA)是一种通过比较各组的均值和方差来分析组间分布差异的统计模型,该模型由 Ronald Fisher 提出。方差分析提供了对多个组的均值是否相等的统计检验,因此将 t 检验推广到两个以上的组。
方差分析可用于比较三个或更多组的统计显着性,因为进行多个双样本 t 检验会导致犯 I 类统计错误的机会增加。
在提供数学解释方面,需要以下内容来理解测试。
x ij = x + (xi − x) + (x ij − x)
这导致以下模型 -
x ij = μ + α i + ε ij
其中 μ 是总平均值,α i是第 i 组平均值。误差项ε ij被假设为正态分布的独立同分布。检验的原假设是 -
α 1 = α 2 = … = α k
在计算检验统计量方面,我们需要计算两个值 -
- 组间差异的平方和 -
$$SSD_B = \sum_{i}^{k} \sum_{j}^{n}(\bar{x_{\bar{i}}} - \bar{x})^2$$
- 组内的平方和
$$SSD_W = \sum_{i}^{k} \sum_{j}^{n}(\bar{x_{\bar{ij}}} - \bar{x_{\bar{i}}})^ 2$$
其中SSD B的自由度为k−1,SSD W的自由度为N−k。然后我们可以定义每个指标的均方差。
MS B = SSD B / (k - 1)
MS w = SSD w / (N - k)
最后,ANOVA中的检验统计量定义为上述两个量的比值
F = MS B / MS w
它遵循具有k−1和N−k自由度的F 分布。如果原假设为真,则 F 可能接近 1。否则,组间均方 MSB 可能很大,从而导致 F 值很大。
基本上,方差分析检查总方差的两个来源,并查看哪一部分贡献更大。这就是为什么它被称为方差分析,尽管其目的是比较组均值。
在计算统计数据方面,在 R 中实际上相当简单。以下示例将演示它是如何完成的并绘制结果。
library(ggplot2)
# We will be using the mtcars dataset
head(mtcars)
# mpg cyl disp hp drat wt qsec vs am gear carb
# Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4
# Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4
# Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1
# Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1
# Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2
# Valiant 18.1 6 225 105 2.76 3.460 20.22 1 0 3 1
# Let's see if there are differences between the groups of cyl in the mpg variable.
data = mtcars[, c('mpg', 'cyl')]
fit = lm(mpg ~ cyl, data = mtcars)
anova(fit)
# Analysis of Variance Table
# Response: mpg
# Df Sum Sq Mean Sq F value Pr(>F)
# cyl 1 817.71 817.71 79.561 6.113e-10 ***
# Residuals 30 308.33 10.28
# Signif. codes: 0 *** 0.001 ** 0.01 * 0.05 .
# Plot the distribution
plot(mpg ~ as.factor(cyl), data = mtcars, col = 'deepskyblue3')
该代码将产生以下输出 -
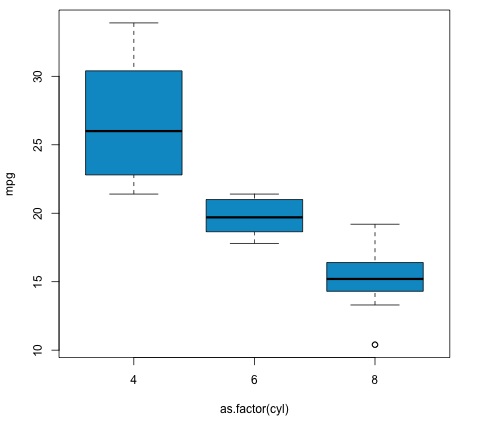
我们在示例中得到的 p 值明显小于 0.05,因此 R 返回符号“***”来表示这一点。这意味着我们拒绝原假设,并且我们发现cyl变量的不同组之间的 mpg 平均值之间存在差异。