密码系统

密码系统是密码技术及其随附基础设施的实现，以提供信息安全服务。密码系统也称为密码系统。

让我们讨论一个简单的密码系统模型，该模型为所传输的信息提供机密性。这个基本模型如下图所示 -

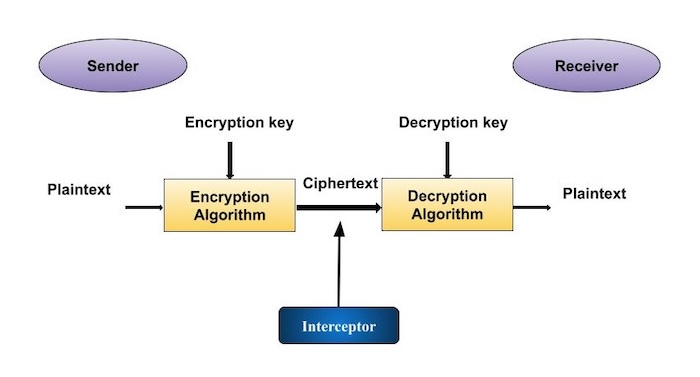
该图显示了发送者想要将一些敏感数据传输到接收者，从而使任何在通信通道上拦截或窃听的一方都无法提取数据。

这个简单密码系统的目标是在过程结束时，只有发送者和接收者会知道明文。

密码系统的组成部分

基本密码系统的各个组件如下 -

纯文本。它是传输过程中要保护的数据。
加密演算法。这是一个为任何给定的明文和加密密钥生成密文的数学过程。它是一种密码算法，以明文和加密密钥作为输入并生成密文。
密文。它是使用特定加密密钥的加密算法产生的明文的加扰版本。密文不受保护。它在公共频道上流动。它可以被任何有权访问通信通道的人拦截或破坏。
解密算法，它是一个数学过程，为任何给定的密文和解密密钥生成唯一的明文。它是一种密码算法，以密文和解密密钥作为输入，并输出明文。解密算法本质上是加密算法的逆过程，因此与加密算法密切相关。
加密密钥。它是发送者已知的值。发送者将加密密钥与明文一起输入加密算法中，以计算密文。
解密密钥。它是接收者已知的值。解密密钥与加密密钥相关，但并不总是相同。接收方将解密密钥与密文一起输入解密算法，以计算明文。

对于给定的密码系统，所有可能的解密密钥的集合称为密钥空间。

拦截者（攻击者）是尝试确定明文的未经授权的实体。他可以看到密文并且可能知道解密算法。然而，他绝不能知道解密密钥。

密码系统的类型

从根本上来说，根据系统中执行加密解密的方式，有两种类型的密码系统 -

对称密钥加密
非对称密钥加密

这些密码系统之间的主要区别在于加密和解密密钥之间的关系。从逻辑上讲，在任何密码系统中，两个密钥都是紧密相关的。使用与加密密钥无关的密钥实际上不可能解密密文。

对称密钥加密

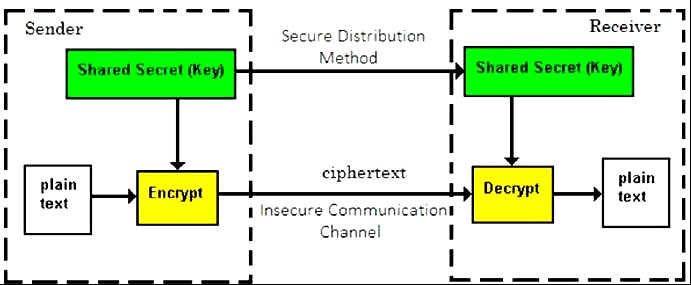
使用相同的密钥来加密和解密信息的加密过程称为对称密钥加密。

对对称密码系统的研究称为对称密码学。对称密码系统有时也称为秘密密钥密码系统。

对称密钥加密方法的一些著名示例包括：数字加密标准 (DES)、三重 DES (3DES)、IDEA 和 BLOWFISH。

1970 年之前，所有密码系统都采用对称密钥加密。即使在今天，它的相关性仍然非常高，并且在许多密码系统中被广泛使用。这种加密不太可能消失，因为它比非对称密钥加密具有某些优势。

基于对称密钥加密的密码系统的显着特征是 -

使用对称密钥加密的人员必须在交换信息之前共享公共密钥。
建议定期更改密钥以防止对系统的任何攻击。
需要存在一个强大的机制来在通信双方之间交换密钥。由于需要定期更换密钥，因此这种机制变得昂贵且麻烦。
在n人的群组中，要实现任意两个人之间的两方通信，群组所需的密钥数量为n × (n – 1)/2。
这种加密中的密钥长度（位数）较小，因此加密-解密过程比非对称密钥加密更快。
运行对称算法所需的计算机系统处理能力较低。

对称密钥密码系统的挑战

使用对称密钥加密有两个限制性挑战。

密钥建立- 在任何通信之前，发送者和接收者都需要就秘密对称密钥达成一致。它需要适当的安全密钥建立机制。
信任问题- 由于发送者和接收者使用相同的对称密钥，因此隐含要求发送者和接收者相互“信任”。例如，可能会发生接收者丢失了攻击者的密钥而发送者没有得到通知的情况。

这两个挑战极大地限制了现代通信。今天，人们需要与不熟悉和不信任的各方交换信息。例如，在线卖家和客户之间的通信。对称密钥加密的这些局限性催生了非对称密钥加密方案。

非对称密钥加密

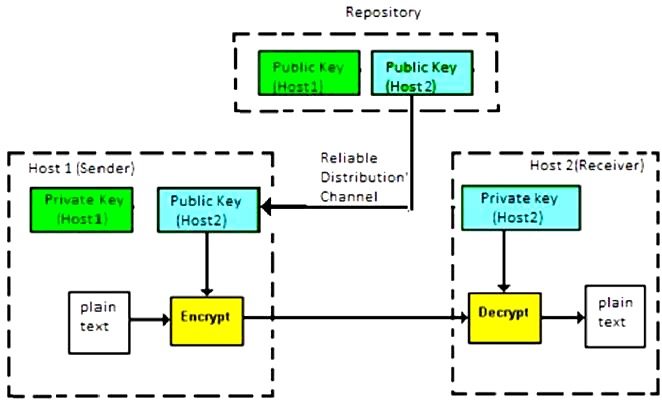
使用不同密钥来加密和解密信息的加密过程称为非对称密钥加密。尽管密钥不同，但它们在数学上是相关的，因此通过解密密文来检索明文是可行的。该过程如下图所示 -

非对称密钥加密是在 20 世纪发明的，^旨在解决通信者之间预先共享密钥的必要性。该加密方案的显着特点如下 -

该系统中的每个用户都需要拥有一对不同的密钥，即私钥和公钥。这些密钥在数学上是相关的——当一个密钥用于加密时，另一个密钥可以将密文解密回原始明文。
它要求将公钥放在公共存储库中，并将私钥作为严格保密的秘密。因此，这种加密方案也称为公钥加密。
尽管用户的公钥和私钥是相关的，但从计算上来说从另一个找到一个是不可行的。这是该方案的优势。
当Host1需要向Host2发送数据时，他从存储库中获取Host2的公钥，对数据进行加密后进行传输。
Host2使用他的私钥来提取明文。
这种加密中的密钥长度（位数）很大，因此加密-解密过程比对称密钥加密慢。
运行非对称算法所需的计算机系统处理能力较高。

对称密码系统是一个自然的概念。相比之下，公钥密码系统相当难以理解。

你可能会想，加密密钥和解密密钥怎么可能有“关联”，但又无法从加密密钥确定解密密钥呢？答案在于数学概念。可以设计一个其密钥具有此属性的密码系统。公钥密码学的概念相对较新。已知的公钥算法比对称算法少。

公钥密码系统的挑战

公钥密码系统面临一个重大挑战——用户需要相信他在与某人通信时使用的公钥确实是该人的公钥，并且没有被恶意第三方欺骗。

这通常是通过由受信任的第三方组成的公钥基础设施 (PKI) 来完成的。第三方安全地管理和证明公钥的真实性。当第三方被要求为任何通信者X提供公钥时，他们被信任提供正确的公钥。

第三方通过证明、公证或其他一些过程来满足用户身份的要求 - X 是唯一的或全局唯一的 X。使经过验证的公钥可用的最常见方法是嵌入它们在由受信任的第三方进行数字签名的证书中。

加密方案之间的关系

下面给出了两种类型的密码系统的基本关键属性的摘要 -

	对称密码系统	公钥密码系统
键之间的关系	相同的	不同，但在数学上相关
加密密钥	对称	民众
解密密钥	对称	私人的

由于两种系统各有优缺点，在实际的信息安全系统中，对称密钥和公钥密码系统经常一起使用。

Kerckhoff 密码系统原理

19 世纪^，荷兰密码学家 A. Kerckhoff 提出了良好密码系统的要求。Kerckhoff 表示，即使系统的所有内容（除了密钥之外）都是公共知识，加密系统也应该是安全的。Kerckhoff 为密码系统定义的六项设计原则是 -

即使在数学上不是这样，密码系统实际上也应该是牢不可破的。
密码系统落入入侵者手中不应导致系统受到任何损害，从而防止给用户带来任何不便。
密钥应该易于传达、记忆且可更改。
密文应该可以通过电报（一种不安全的通道）传输。
加密装置和文件应当是便携式的并且可由一个人操作。
最后，该系统必须易于使用，既不需要精神紧张，也不需要了解一系列要遵守的规则。

第二条规则目前被称为柯克霍夫原则。它几乎应用于所有当代加密算法，例如 DES、AES 等。这些公共算法被认为是完全安全的。加密消息的安全性仅取决于秘密加密密钥的安全性。

保持算法的秘密可能会成为密码分析的一个重要障碍。然而，只有当算法在严格限制的范围内使用时，才可能使算法保密。

在现代，密码学需要迎合连接到互联网的用户。在这种情况下，使用秘密算法是不可行的，因此 Kerckhoff 原理成为现代密码学中设计算法的基本准则。