离散数学 - 快速指南
离散数学 - 简介
数学可大致分为两类 -
连续数学- 它基于连续数轴或实数。它的特点是,任意两个数之间,几乎总是存在无限个数集。例如,连续数学中的函数可以绘制成不间断的平滑曲线。
离散数学-它涉及不同的值;即任意两点之间,存在可数个点。例如,如果我们有一组有限的对象,则该函数可以定义为具有这些对象的有序对的列表,并且可以呈现为这些对的完整列表。
离散数学专题
尽管离散数学的分支数量不固定,但有关此问题的任何研究几乎总是涵盖以下主题 -
- 集合、关系和函数
- 数理逻辑
- 群论
- 计数理论
- 可能性
- 数学归纳法和递归关系
- 图论
- 树木
- 布尔代数
我们将在本教程的后续章节中讨论每个概念。
离散数学 - 集合
德国数学家G.康托尔提出了集合的概念。他将集合定义为通过某些规则或描述选择的明确且可区分的对象的集合。
集合论构成了其他几个研究领域的基础,例如计数理论、关系、图论和有限状态机。在本章中,我们将介绍集合论的不同方面。
集合 - 定义
集合是不同元素的无序集合。可以通过使用集合括号列出其元素来显式地编写集合。如果元素的顺序发生更改或集合中的任何元素重复,则不会对集合进行任何更改。
集合的一些例子
- 所有正整数的集合
- 太阳系中所有行星的集合
- 印度所有州的集合
- 字母表中所有小写字母的集合
集合的表示
集合可以用两种方式表示 -
- 名册或表格形式
- 集合生成器符号
名册或表格形式
该集合通过列出组成它的所有元素来表示。元素括在大括号内并用逗号分隔。
示例 1 - 英语字母表中的元音集,$A = \lbrace a,e,i,o,u \rbrace$
示例 2 - 小于 10 的奇数集,$B = \lbrace 1,3,5,7,9 \rbrace$
集合生成器符号
该集合是通过指定该集合的元素所共有的属性来定义的。该集合被描述为 $A = \lbrace x : p(x) \rbrace$
示例 1 - 集合 $\lbrace a,e,i,o,u \rbrace$ 写为 -
$A = \lbrace x : \text{x 是英文字母中的元音} \rbrace$
示例 2 - 集合 $\lbrace 1,3,5,7,9 \rbrace$ 写为 -
$B = \lbrace x : 1 \le x \lt 10 \ and\ (x \% 2) \ne 0 \rbrace$
如果元素 x 是任意集合 S 的成员,则用 $x \in S$ 表示,如果元素 y 不是集合 S 的成员,则用 $y \notin S$ 表示。
示例-如果 $S = \lbrace1, 1.2, 1.7, 2\rbrace , 1 \in S$ 但 $1.5 \notin S$
一些重要的集合
N − 所有自然数的集合 = $\lbrace1, 2, 3, 4, .....\rbrace$
Z − 所有整数的集合 = $\lbrace....., -3, -2, -1, 0, 1, 2, 3, .....\rbrace$
Z + − 所有正整数的集合
Q - 所有有理数的集合
R - 所有实数的集合
W - 所有整数的集合
集合的基数
集合 S 的基数,用 $|S|$ 表示,是集合中元素的数量。该数字也称为基数。如果一个集合有无限个元素,它的基数是$\infty$。
示例- $|\lbrace 1, 4, 3, 5 \rbrace | = 4, | \lbrace 1, 2, 3, 4, 5, \点 \rbrace | = \infty$
如果有两个集合X和Y,
$|X| = |Y|$ 表示具有相同基数的两个集合 X 和 Y。当 X 中的元素数量恰好等于 Y 中的元素数量时,就会发生这种情况。在这种情况下,存在从 X 到 Y 的双射函数“f”。
$|X| \le |Y|$ 表示集合 X 的基数小于或等于集合 Y 的基数。当 X 中的元素数量小于或等于 Y 中的元素数量时,就会发生这种情况。这里,存在从 X 到 Y 的单射函数“f”。
$|X| \lt |Y|$ 表示集合 X 的基数小于集合 Y 的基数。当 X 中的元素数量小于 Y 中的元素数量时,就会发生这种情况。这里,从 X 到 Y 的函数“f”是单射函数,但不是双射函数。
$如果\ |X| \le |Y|$ 和 $|X| \ge |Y|$ 然后 $|X| = |Y|$。集合 X 和 Y 通常称为等价集合。
套装类型
集合可以分为多种类型。其中一些是有限集、无限集、子集、全集、真集、单例集等。
有限集
包含一定数量元素的集合称为有限集合。
示例- $S = \lbrace x \:| \:x \in N$ 和 $70 \gt x \gt 50 \rbrace$
无限集
包含无限个元素的集合称为无限集。
示例- $S = \lbrace x \: | \: x \in N $ 和 $ x \gt 10 \rbrace$
子集
如果 X 的每个元素都是集合 Y 的元素,则集合 X 是集合 Y 的子集(写为 $X \subseteq Y$)。
示例 1 - 让 $X = \lbrace 1, 2, 3, 4, 5, 6 \rbrace$ 和 $Y = \lbrace 1, 2 \rbrace$。这里集合Y是集合X的子集,因为集合Y的所有元素都在集合X中。因此,我们可以写$Y \subseteq X$。
示例 2 - 让 $X = \lbrace 1, 2, 3 \rbrace$ 和 $Y = \lbrace 1, 2, 3 \rbrace$。这里集合 Y 是集合 X 的子集(不是真子集),因为集合 Y 的所有元素都在集合 X 中。因此,我们可以写 $Y \subseteq X$。
真子集
术语“真子集”可以定义为“但不等于”的子集。如果 X 的每个元素都是集合 Y 的元素且 $|X| ,则集合 X 是集合 Y 的真子集(写为 $ X \subset Y $)\lt |Y|$。
示例- 设 $X = \lbrace 1, 2, 3, 4, 5, 6 \rbrace$ 和 $Y = \lbrace 1, 2 \rbrace$。这里设置$Y \subset X$,因为$Y$中的所有元素也包含在$X$中,并且$X$至少有一个元素比集合$Y$多。
通用套装
它是特定上下文或应用程序中所有元素的集合。该上下文或应用程序中的所有集合本质上都是该通用集合的子集。通用集表示为 $U$。
示例- 我们可以将 $U$ 定义为地球上所有动物的集合。在这种情况下,所有哺乳动物的集合是 $U$ 的子集,所有鱼类的集合是 $U$ 的子集,所有昆虫的集合是 $U$ 的子集,依此类推。
空集或零集
空集不包含任何元素。它用$\emptyset$ 表示。由于空集的元素个数是有限的,所以空集是有限集。空集或空集的基数为零。
示例- $S = \lbrace x \:| \: x \in N$ 和 $7 \lt x \lt 8 \rbrace = \emptyset$
单例集或单元集
单例集或单元集仅包含一个元素。单例集用 $\lbrace s \rbrace$ 表示。
示例- $S = \lbrace x \:| \:x \in N,\ 7 \lt x \lt 9 \rbrace$ = $\lbrace 8 \rbrace$
等集
如果两个集合包含相同的元素,则称它们相等。
示例- 如果 $A = \lbrace 1, 2, 6 \rbrace$ 和 $B = \lbrace 6, 1, 2 \rbrace$,则它们相等,因为集合 A 的每个元素都是集合 B 的元素,并且集合 A 的每个元素都是集合 B 的元素集合B是集合A的元素。
等效组
如果两个集合的基数相同,则称它们为等价集合。
示例- 如果 $A = \lbrace 1, 2, 6 \rbrace$ 和 $B = \lbrace 16, 17, 22 \rbrace$,它们是等效的,因为 A 的基数等于 B 的基数。即 $|A | =|B| = 3$
重叠集
至少有一个公共元素的两个集合称为重叠集合。
如果集合重叠 -
$n(A \cup B) = n(A) + n(B) - n(A \cap B)$
$n(A \cup B) = n(A - B) + n(B - A) + n(A \cap B)$
$n(A) = n(A - B) + n(A \cap B)$
$n(B) = n(B - A) + n(A \cap B)$
示例- 设 $A = \lbrace 1, 2, 6 \rbrace$ 和 $B = \lbrace 6, 12, 42 \rbrace$。有一个公共元素“6”,因此这些集合是重叠集合。
不相交集
如果两个集合 A 和 B 甚至没有一个共同元素,则这两个集合称为不相交集合。因此,不相交集具有以下属性 -
$n(A \cap B) = \emptyset$
$n(A \杯子 B) = n(A) + n(B)$
示例- 假设 $A = \lbrace 1, 2, 6 \rbrace$ 和 $B = \lbrace 7, 9, 14 \rbrace$,没有单个公共元素,因此这些集合是重叠集合。
维恩图
维恩图,由约翰·维恩于1880年发明,是一种显示不同数学集合之间所有可能的逻辑关系的示意图。
例子
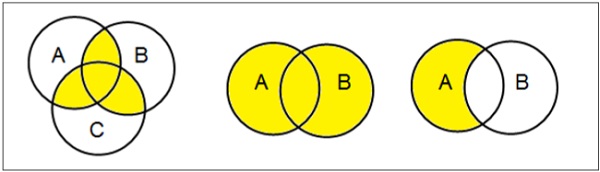
设置操作
集合运算包括集合并、集合交、集合差、集合补和笛卡尔积。
集合联盟
集合 A 和 B 的并集(表示为 $A \cup B$)是 A 中、B 中或 A 和 B 中的元素的集合。因此,$A \cup B = \lbrace x \: | \: x \in A\ OR\ x \in B \rbrace$。
示例- 如果 $A = \lbrace 10, 11, 12, 13 \rbrace$ 且 B = $\lbrace 13, 14, 15 \rbrace$,则 $A \cup B = \lbrace 10, 11, 12, 13, 14, 15 \rbrace$。(公共元素只出现一次)
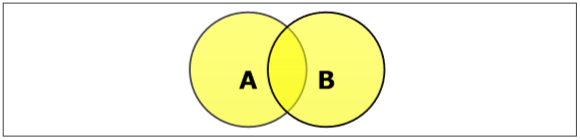
设置交集
集合 A 和 B 的交集(记为 $A \cap B$)是同时位于 A 和 B 中的元素的集合。因此,$A \cap B = \lbrace x \:|\: x \in A \ AND\ x \in B \rbrace$。
示例- 如果 $A = \lbrace 11, 12, 13 \rbrace$ 且 $B = \lbrace 13, 14, 15 \rbrace$,则 $A \cap B = \lbrace 13 \rbrace$。
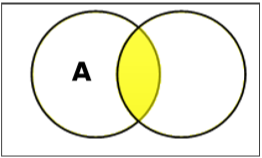
设置差异/相对补集
集合 A 和 B 的集合差(记为 $A – B$)是只在 A 中而不在 B 中的元素的集合。因此,$A - B = \lbrace x \:| \: x \in A\ AND\ x \not B \rbrace$。
示例- 如果 $A = \lbrace 10, 11, 12, 13 \rbrace$ 且 $B = \lbrace 13, 14, 15 \rbrace$,则 $(A - B) = \lbrace 10, 11, 12 \rbrace $ 和 $(B - A) = \lbrace 14, 15 \rbrace$。在这里,我们可以看到 $(A - B) \ne (B - A)$
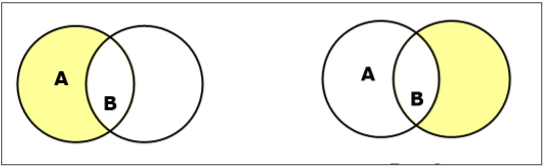
集合的补集
集合 A 的补集(用 $A'$ 表示)是不在集合 A 中的元素的集合。因此,$A' = \lbrace x | x \notin A \rbrace$。
更具体地说,$A'= (U - A)$,其中$U$ 是包含所有对象的通用集。
示例- 如果 $A = \lbrace x \:| \: x\ \: {属于奇数整数的集合} \rbrace$ 则 $A' = \lbrace y\: | \: y\ \: {不属于\: 奇数整数的集合} \rbrace$
笛卡尔积/叉积
n 个集合 $A_1, A_2, \dots A_n$ 的笛卡尔积表示为 $A_1 \times A_2 \dots \times A_n$ 可以定义为所有可能的有序对 $(x_1, x_2, \dots x_n)$ 其中$x_1 \在 A_1 中,x_2 \在 A_2 中,\点 x_n \在 A_n$ 中
示例- 如果我们采用两个集合 $A = \lbrace a, b \rbrace$ 和 $B = \lbrace 1, 2 \rbrace$,
A 和 B 的笛卡尔积写为 − $A \times B = \lbrace (a, 1), (a, 2), (b, 1), (b, 2)\rbrace$
B 和 A 的笛卡尔积写为 − $B \times A = \lbrace (1, a), (1, b), (2, a), (2, b)\rbrace$
电源组
集合S的幂集是S的所有子集(包括空集)的集合。基数为 n 的集合 S 的幂集的基数为 $2^n$。幂集表示为$P(S)$。
示例 -
对于集合 $S = \lbrace a, b, c, d \rbrace$ 让我们计算子集 -
具有 0 个元素的子集 - $\lbrace \emptyset \rbrace$ (空集)
具有 1 个元素的子集 - $\lbrace a \rbrace、\lbrace b \rbrace、\lbrace c \rbrace、\lbrace d \rbrace$
具有 2 个元素的子集 - $\lbrace a, b \rbrace, \lbrace a,c \rbrace, \lbrace a, d \rbrace, \lbrace b, c \rbrace, \lbrace b,d \rbrace,\lbrace c, d \r大括号$
具有 3 个元素的子集 - $\lbrace a ,b, c\rbrace,\lbrace a, b, d \rbrace, \lbrace a,c,d \rbrace,\lbrace b,c,d \rbrace$
具有 4 个元素的子集 - $\lbrace a, b, c, d \rbrace$
因此,$P(S)=$
$\lbrace \quad \lbrace \emptyset \rbrace、\lbrace a \rbrace、\lbrace b \rbrace、\lbrace c \rbrace、\lbrace d \rbrace、\lbrace a,b \rbrace、\lbrace a,c \ rbrace, \lbrace a,d \rbrace, \lbrace b,c \rbrace, \lbrace b,d \rbrace, \lbrace c,d \rbrace, \lbrace a,b,c \rbrace, \lbrace a,b, d \rbrace, \lbrace a,c,d \rbrace, \lbrace b,c,d \rbrace, \lbrace a,b,c,d \rbrace \quad \rbrace$
$| P(S)| = 2^4 = 16$
注意- 空集的幂集也是空集。
$| P (\lbrace \emptyset \rbrace) | P (\lbrace \emptyset \rbrace) | = 2^0 = 1$
集合的划分
一个集合的划分,比如S ,是n 个不相交子集的集合,比如 $P_1, P_2, \dots P_n$ 满足以下三个条件 -
$P_i$ 不包含空集。
$\lbrack P_i \ne \lbrace \emptyset \rbrace\ for\ all\ 0 \lt i \le n \rbrack$
子集的并集必须等于整个原始集。
$\lbrack P_1 \cup P_2 \cup \dots \cup P_n = S \rbrack$
任何两个不同集合的交集都是空的。
$\lbrack P_a \cap P_b = \lbrace \emptyset \rbrace,\ for\ a \ne b\ 其中\ n \ge a,\: b \ge 0 \rbrack$
例子
设 $S = \lbrace a, b, c, d, e, f, g, h \rbrace$
一种可能的分区是 $\lbrace a \rbrace, \lbrace b, c, d \rbrace, \lbrace e, f, g, h \rbrace$
另一个可能的分区是 $\lbrace a, b \rbrace, \lbrace c, d \rbrace, \lbrace e, f, g, h \rbrace$
铃声号码
贝尔数给出了划分集合的方法的数量。它们用 $B_n$ 表示,其中 n 是集合的基数。
示例-
设 $S = \lbrace 1, 2, 3\rbrace$, $n = |S| = 3$
备用分区是 -
1. $\emptyset , \lbrace 1, 2, 3 \rbrace$
2. $\lbrace 1 \rbrace , \lbrace 2, 3 \rbrace$
3. $\lbrace 1, 2 \rbrace , \lbrace 3 \rbrace$
4. $\lbrace 1, 3 \rbrace , \lbrace 2 \rbrace$
5. $\lbrace 1 \rbrace , \lbrace 2 \rbrace , \lbrace 3 \rbrace$
因此 $B_3 = 5$
离散数学 - 关系
每当讨论集合时,接下来就会出现集合元素之间的关系。关系可以存在于同一集合的对象之间或者两个或多个集合的对象之间。
定义和属性
从集合 x 到 y 的二元关系 R(写为 $xRy$ 或 $R(x,y)$)是笛卡尔积 $x \times y$ 的子集。如果 G 的有序对颠倒,关系也会改变。
通常,集合 $A_1、\dots 、\ 和\ A_n$ 之间的 n 元关系 R 是 n 元乘积 $A_1 \times \dots \times A_n$ 的子集。在这种情况下,关系 R 的最小基数为零,最大基数为 $n^2$。
单个集合 A 上的二元关系 R 是 $A \times A$ 的子集。
对于两个不同的集合 A 和 B,分别具有基数m和n,从 A 到 B 的关系 R 的最大基数是mn。
域和范围
如果有两个集合 A 和 B,且关系 R 具有阶对 (x, y),则 -
R 的定义域Dom(R) 是集合 $\lbrace x \:| \: (x, y) \in R \:对于某些\: y\: in\: B \rbrace$
R 的范围Ran(R) 是集合 $\lbrace y\: |\: (x, y) \in R \:for\: some\: x\: in\: A\rbrace $
例子
让 $A = \lbrace 1, 2, 9 \rbrace $ 和 $ B = \lbrace 1, 3, 7 \rbrace$
情况 1 - 如果关系 R “等于”,则 $R = \lbrace (1, 1), (3, 3) \rbrace$
Dom(R) = $\lbrace 1, 3 \rbrace , Ran(R) = \lbrace 1, 3 \rbrace$
情况 2 - 如果关系 R 为“小于”,则 $R = \lbrace (1, 3), (1, 7), (2, 3), (2, 7) \rbrace$
Dom(R) = $\lbrace 1, 2 \rbrace , Ran(R) = \lbrace 3, 7 \rbrace$
情况 3 - 如果关系 R “大于”,则 $R = \lbrace (2, 1), (9, 1), (9, 3), (9, 7) \rbrace$
Dom(R) = $\lbrace 2, 9 \rbrace , Ran(R) = \lbrace 1, 3, 7 \rbrace$
使用图表示关系
关系可以使用有向图来表示。
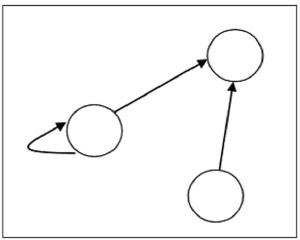
图中的顶点数等于定义关系的集合中的元素数。对于关系 R 中的每个有序对 (x, y),都会有一条从顶点“x”到顶点“y”的有向边。如果存在有序对(x,x),则顶点x上将存在自环。
假设,集合 $S = \lbrace 1, 2, 3 \rbrace$ 上存在关系 $R = \lbrace (1, 1), (1,2), (3, 2) \rbrace$,则可以为由下图表示 -
关系类型
集合 X 和 Y 之间或 E 上的空关系是空集合 $\emptyset$
集合 X 和 Y 之间的完整关系是集合 $X \times Y$
集合 X 上的恒等关系是集合 $\lbrace (x, x) | x \in X \rbrace$
关系 R 的逆关系 R' 定义为 − $R' = \lbrace (b, a) | (a, b) \in R \rbrace$
示例- 如果 $R = \lbrace (1, 2), (2, 3) \rbrace$ 则 $R' $ 将是 $\lbrace (2, 1), (3, 2) \rbrace$
如果 $\forall a \in A$ 与 a 相关(aRa 成立),则集合A 上的关系 R 称为自反关系
示例- 集合 $X = \lbrace a, b \rbrace$ 上的关系 $R = \lbrace (a, a), (b, b) \rbrace$ 是自反的。
如果 A$ 中没有 $a \in A$ 与 a 相关(aRa 不成立),则集合 A上的关系 R 称为Irreflexive 。
示例- 集合 $X = \lbrace a, b \rbrace$ 上的关系 $R = \lbrace (a, b), (b, a) \rbrace$ 是反反的。
如果 $xRy$ 暗示 $yRx$、$\forall x \in A$ 和 $\forall y \in A$ ,则集合 A 上的关系 R 称为对称关系。
示例- 集合 $A = \lbrace 1, 2, 3 \rbrace$ 上的关系 $R = \lbrace (1, 2), (2, 1), (3, 2), (2, 3) \rbrace$是对称的。
如果 $xRy$ 和 $yRx$ 意味着 $x = y \: \forall x \in A$ 和 $\forall y \in A$,则集合 A 上的关系 R 称为反对称关系。
示例- 关系 $R = \lbrace (x, y)\to N |\:x \leq y \rbrace$ 是反对称的,因为 $x \leq y$ 和 $y \leq x$ 意味着 $x = y $。
如果 $xRy$ 和 $yRz$ 暗示 $xRz,\forall x,y,z \in A$,则集合 A上的关系 R 称为传递性的。
示例- 集合 $A = \lbrace 1, 2, 3 \rbrace$ 上的关系 $R = \lbrace (1, 2), (2, 3), (1, 3) \rbrace$ 是传递的。
如果关系是自反、对称和传递的,则该关系是等价关系。
示例- 关系 $R = \lbrace (1, 1), (2, 2), (3, 3), (1, 2), (2,1), (2,3), (3,2) , (1,3), (3,1) \rbrace$ 在集合 $A = \lbrace 1, 2, 3 \rbrace$ 上是一个等价关系,因为它是自反、对称和传递的。
离散数学 - 函数
函数将相关集合中的一个元素准确地分配给集合中的每个元素。函数在各个领域都有应用,例如算法计算复杂性的表示、对象计数、序列和字符串的研究等等。本部分的第三章也是最后一章强调了函数的重要方面。
功能 - 定义
函数或映射(定义为 $f: X \rightarrow Y$)是从一个集合 X 的元素到另一个集合 Y 的元素的关系(X 和 Y 是非空集合)。X 称为域,Y 称为函数“f”的余域。
函数“f”是 X 和 Y 上的关系,使得对于 X$ 中的每个 $x,Y$ 中存在唯一的 $y,使得 R$ 中的 $(x,y) \in R$。“x”称为原像,“y”称为函数 f 的图像。
函数可以是一对一或多对一,但不能是一对多。
单射/一对一函数
函数 $f: A \rightarrow B$ 是单射函数或一对一函数,如果对于每个 $b \in B$,最多存在一个 $a \in A$ 使得 $f(s) = t$ 。
这意味着如果 $a_1 \ne a_2$ 暗示 $f(a1) \ne f(a2)$,则函数f是单射的。
例子
$f: N \rightarrow N, f(x) = 5x$ 是单射的。
$f: N \rightarrow N, f(x) = x^2$ 是单射的。
$f: R\rightarrow R, f(x) = x^2$ 不是单射的,因为 $(-x)^2 = x^2$
满射/本体函数
如果 f 的像等于其范围,则函数 $f: A \rightarrow B$ 是满射的。等价地,对于每个$b \in B$,都存在一些$a \in A$,使得$f(a) = b$。这意味着对于 B 中的任意 y,A 中存在某个 x 使得 $y = f(x)$。
例子
$f : N \rightarrow N, f(x) = x + 2$ 是满射。
$f : R \rightarrow R, f(x) = x^2$ 不是满射,因为我们找不到平方为负的实数。
双射/一对一通讯员
函数 $f: A \rightarrow B$ 是双射或一一对应的当且仅当f既是单射又是满射。
问题
证明由 $f(x) = 2x – 3$ 定义的函数 $f: R \rightarrow R$ 是双射函数。
解释- 我们必须证明这个函数既是单射的又是满射的。
如果 $f(x_1) = f(x_2)$,则 $2x_1 – 3 = 2x_2 – 3 $,这意味着 $x_1 = x_2$。
因此,f 是单射的。
这里,$2x – 3= y$
因此,$x = (y+5)/3$ 属于 R,$f(x) = y$。
因此,f 是满射的。
由于f既是满射又是单射,我们可以说f是双射的。
函数的反函数
一对一对应函数 $f : A \rightarrow B$ 的逆函数是函数 $g : B \rightarrow A$,具有以下属性 -
$f(x) = y \Leftrightarrow g(y) = x$
如果函数 f的反函数 g 存在,则函数f 称为可逆的。
例子
函数 $f : Z \rightarrow Z, f(x)=x+5$ 是可逆的,因为它具有反函数 $ g : Z \rightarrow Z, g(x)= x-5$。
函数 $f : Z \rightarrow Z, f(x)=x^2$ 不可逆,因为它不是一对一的 $(-x)^2=x^2$。
函数的构成
两个函数 $f: A \rightarrow B$ 和 $g: B \rightarrow C$ 可以组合起来给出组合 $gof$。这是由 $(gof)(x) = g(f(x))$ 定义的从 A 到 C 的函数
例子
令$f(x) = x + 2$ 和$g(x) = 2x + 1$,找到$(fog)(x)$ 和$(gof)(x)$。
解决方案
$(雾)(x) = f (g(x)) = f(2x + 1) = 2x + 1 + 2 = 2x + 3$
$(gof)(x) = g (f(x)) = g(x + 2) = 2 (x+2) + 1 = 2x + 5$
因此,$(fog)(x) \neq (gof)(x)$
关于构图的一些事实
如果 f 和 g 是一对一的,那么函数 $(gof)$ 也是一对一的。
如果 f 和 g 是 on 则函数 $(gof)$ 也是 on。
组合总是具有结合性,但不具有交换性。
离散数学-命题逻辑
数理逻辑规则指定了数学陈述的推理方法。希腊哲学家亚里士多德是逻辑推理的先驱。逻辑推理为数学乃至计算机科学的许多领域提供了理论基础。它在计算机科学中有许多实际应用,如计算机器设计、人工智能、编程语言数据结构的定义等。
命题逻辑涉及可以分配真值“真”和“假”的陈述。目的是单独或以综合方式分析这些陈述。
介词逻辑 – 定义
命题是具有真值“真”或真值“假”的陈述性陈述的集合。命题由命题变量和连接词组成。我们用大写字母(A、B等)表示命题变量。连接词连接命题变量。
下面给出了一些命题示例 -
- “Man is Mortal”,它返回真值“TRUE”
- “12 + 9 = 3 – 2”,返回真值“FALSE”
以下不是提案 -
“A小于2”。这是因为除非我们给出 A 的具体值,否则我们无法判断该陈述是真还是假。
连接词
在命题逻辑中,我们通常使用五个连接词,它们是 -
或 ($\lor$)
和($\土地$)
否定/非 ($\lnot$)
蕴涵 / if-then ($\rightarrow$)
当且仅当 ($\Leftrightarrow$)。
OR ($\lor$) - 如果命题变量 A 或 B 中至少有一个为真,则两个命题 A 和 B(写为 $A \lor B$)的 OR 运算为真。
真值表如下 -
| A | 乙 | A ∨ B |
|---|---|---|
| 真的 | 真的 | 真的 |
| 真的 | 错误的 | 真的 |
| 错误的 | 真的 | 真的 |
| 错误的 | 错误的 | 错误的 |
AND ($\land$) - 如果命题变量 A 和 B 都为真,则两个命题 A 和 B(写为 $A \land B$)的 AND 运算为真。
真值表如下 -
| A | 乙 | A∧B |
|---|---|---|
| 真的 | 真的 | 真的 |
| 真的 | 错误的 | 错误的 |
| 错误的 | 真的 | 错误的 |
| 错误的 | 错误的 | 错误的 |
否定 ($\lnot$) - 命题 A 的否定(写为 $\lnot A$)在 A 为真时为假,在 A 为假时为真。
真值表如下 -
| A | Ø A |
|---|---|
| 真的 | 错误的 |
| 错误的 | 真的 |
蕴涵 / if-then ($\rightarrow$) - 蕴涵 $A \rightarrow B$ 是命题“如果 A,则 B”。如果 A 为真且 B 为假,则为假。其余情况均为真。
真值表如下 -
| A | 乙 | 甲 → 乙 |
|---|---|---|
| 真的 | 真的 | 真的 |
| 真的 | 错误的 | 错误的 |
| 错误的 | 真的 | 真的 |
| 错误的 | 错误的 | 真的 |
当且仅当 ($ \Leftrightarrow $) − $A \Leftrightarrow B$ 是双条件逻辑连接词,当 p 和 q 相同时为真,即两者都为假或两者都为真。
真值表如下 -
| A | 乙 | A⇔B |
|---|---|---|
| 真的 | 真的 | 真的 |
| 真的 | 错误的 | 错误的 |
| 错误的 | 真的 | 错误的 |
| 错误的 | 错误的 | 真的 |
同义反复
同义反复是一个对其命题变量的每个值都始终成立的公式。
示例- 证明 $\lbrack (A \rightarrow B) \land A \rbrack \rightarrow B$ 是同义反复
真值表如下 -
| A | 乙 | 甲 → 乙 | (A → B) ∧ A | [( A → B ) ∧ A] → B |
|---|---|---|---|---|
| 真的 | 真的 | 真的 | 真的 | 真的 |
| 真的 | 错误的 | 错误的 | 错误的 | 真的 |
| 错误的 | 真的 | 真的 | 错误的 | 真的 |
| 错误的 | 错误的 | 真的 | 错误的 | 真的 |
我们可以看到 $\lbrack (A \rightarrow B) \land A \rbrack \rightarrow B$ 的每个值都是“True”,这是一个同义反复。
矛盾之处
矛盾是一个对于其命题变量的每个值都始终为假的公式。
示例- 证明 $(A \lor B) \land \lbrack ( \lnot A) \land (\lnot B) \rbrack$ 是矛盾
真值表如下 -
| A | 乙 | A ∨ B | Ø A | Ø B | (-A) ∧ (-B) | (A ∨ B) ∧ [( Ø A) ∧ (Ø B)] |
|---|---|---|---|---|---|---|
| 真的 | 真的 | 真的 | 错误的 | 错误的 | 错误的 | 错误的 |
| 真的 | 错误的 | 真的 | 错误的 | 真的 | 错误的 | 错误的 |
| 错误的 | 真的 | 真的 | 真的 | 错误的 | 错误的 | 错误的 |
| 错误的 | 错误的 | 错误的 | 真的 | 真的 | 真的 | 错误的 |
我们可以看到 $(A \lor B) \land \lbrack ( \lnot A) \land (\lnot B) \rbrack$ 的每个值都是“False”,这是一个矛盾。
意外事件
偶然性是一个公式,它的命题变量的每个值都有一些真值和一些假值。
示例- 证明 $(A \lor B) \land (\lnot A)$ 是一个意外事件
真值表如下 -
| A | 乙 | A ∨ B | Ø A | (A ∨ B) ∧ (← A) |
|---|---|---|---|---|
| 真的 | 真的 | 真的 | 错误的 | 错误的 |
| 真的 | 错误的 | 真的 | 错误的 | 错误的 |
| 错误的 | 真的 | 真的 | 真的 | 真的 |
| 错误的 | 错误的 | 错误的 | 真的 | 错误的 |
我们可以看到 $(A \lor B) \land (\lnot A)$ 的每个值都有“True”和“False”,这是一个偶然性。
命题等价
如果满足以下两个条件中的任何一个,则两个语句 X 和 Y 在逻辑上是等价的 -
每个语句的真值表具有相同的真值。
双条件语句 $X \Leftrightarrow Y$ 是同义反复。
示例- 证明 $\lnot (A \lor B) 和 \lbrack (\lnot A) \land (\lnot B) \rbrack$ 是等价的
通过第一种方法测试(匹配真值表)
| A | 乙 | A ∨ B | ← (A ∨ B) | Ø A | Ø B | [(-A)∧(-B)] |
|---|---|---|---|---|---|---|
| 真的 | 真的 | 真的 | 错误的 | 错误的 | 错误的 | 错误的 |
| 真的 | 错误的 | 真的 | 错误的 | 错误的 | 真的 | 错误的 |
| 错误的 | 真的 | 真的 | 错误的 | 真的 | 错误的 | 错误的 |
| 错误的 | 错误的 | 错误的 | 真的 | 真的 | 真的 | 真的 |
在这里,我们可以看到 $\lnot (A \lor B) 和 \lbrack (\lnot A) \land (\lnot B) \rbrack$ 的真值相同,因此语句是等价的。
通过第二种方法测试(双条件)
| A | 乙 | ← (A ∨ B ) | [(-A)∧(-B)] | [Ø (A ∨ B)] ⇔ [(Ø A ) ∧ (Ø B)] |
|---|---|---|---|---|
| 真的 | 真的 | 错误的 | 错误的 | 真的 |
| 真的 | 错误的 | 错误的 | 错误的 | 真的 |
| 错误的 | 真的 | 错误的 | 错误的 | 真的 |
| 错误的 | 错误的 | 真的 | 真的 | 真的 |
由于 $\lbrack \lnot (A \lor B) \rbrack \Leftrightarrow \lbrack (\lnot A ) \land (\lnot B) \rbrack$ 是同义反复,因此语句是等效的。
逆、逆、反正
蕴涵 / if-then $(\rightarrow)$ 也称为条件语句。它有两个部分 -
- 假设,p
- 结论,q
如前所述,它被表示为$p \rightarrow q$。
条件语句示例- “如果你做了作业,你就不会受到惩罚。” 这里,“你做了你的作业”是假设,p,“你不会受到惩罚”是结论,q。
逆- 条件语句的逆是假设和结论的否定。如果语句是“If p, then q”,则逆命题将是“If not p, then not q”。因此 $p \rightarrow q$ 的逆是 $ \lnot p \rightarrow \lnot q$。
示例- “如果你做作业,你不会受到惩罚”的反义词是“如果你不做作业,你就会受到惩罚”。
Converse - 条件语句的逆是通过交换假设和结论来计算的。如果语句是“If p, then q”,则相反的语句是“If q, then p”。$p \rightarrow q$ 的逆矩阵是 $q \rightarrow p$。
示例- “如果你做了你的作业,你就不会受到惩罚”的反义词是“如果你不会受到惩罚,你就会做你的作业”。
反正-条件的反正是通过交换假设和逆命题的结论来计算的。如果陈述是“如果p,则q”,则其逆命题将是“如果不是q,则不是p”。$p \rightarrow q$ 的逆否是 $\lnot q \rightarrow \lnot p$。
示例- “如果你做了作业,你就不会受到惩罚”的反证是“如果你受到惩罚,你就没有做作业”。
对偶原理
对偶原理指出,对于任何真命题,通过将并集互换为交集(反之亦然)以及将全集互换为空集(反之亦然)而获得的对偶命题也为真。如果任何语句的对偶是该语句本身,则称为自对偶语句。
示例- $(A \cap B ) \cup C$ 的对偶是 $(A \cup B) \cap C$
范式
我们可以将任何命题转换为两种范式 -
- 连词范式
- 析取范式
连接范式
如果复合语句是通过用 OR 连接的变量(包括变量的否定)进行 AND 运算而得到的,则该复合语句是合取范式。从集合运算的角度来看,它是通过并联连接的变量之间进行交集得到的复合语句。
例子
$(A \lor B) \land (A \lor C) \land (B \lor C \lor D)$
$(P \cup Q) \cap (Q \cup R)$
析取范式
如果复合语句是通过与连接的变量(包括变量的否定)之间的或操作而获得的,则该复合语句是析取范式。从集合运算的角度来看,它是通过交集连接的变量之间通过Union得到的复合语句。
例子
$(A \land B) \lor (A \land C) \lor (B \land C \land D)$
$(P \cap Q) \cup (Q \cap R)$
离散数学 - 谓词逻辑
谓词逻辑处理谓词,即包含变量的命题。
谓词逻辑 – 定义
谓词是在某个特定域上定义的一个或多个变量的表达式。带有变量的谓词可以通过给变量赋值或量化变量来构成命题。
以下是谓词的一些示例 -
- 设 E(x, y) 表示“x = y”
- 设 X(a, b, c) 表示“a + b + c = 0”
- 设 M(x, y) 表示“x 与 y 结婚”
结构良好的公式
格式良好的公式 (wff) 是包含以下任意一项的谓词 -
所有命题常量和命题变量都是 wffs
如果 x 是变量且 Y 是 wff,则 $\forall x Y$ 和 $\exists x Y$ 也是 wff
真值和假值是wffs
每个Atomics式都是一个wff
所有连接 wff 的连接词都是 wff
量词
谓词的变量由量词来量化。谓词逻辑中有两种类型的量词 - 通用量词和存在量词。
通用量词
通用量词指出,其范围内的陈述对于特定变量的每个值都成立。它由符号$\forall$ 表示。
$\forall x P(x)$ 被读取为对于 x 的每个值,P(x) 都为 true。
示例- “人是终有一死的”可以转化为命题形式 $\forall x P(x)$,其中 P(x) 是谓词,表示 x 是终有一死的,并且话语的宇宙是所有人。
存在量词
存在量词指出其范围内的陈述对于特定变量的某些值是正确的。它由符号$\exists $ 表示。
$\exists x P(x)$ 被读取为对于 x 的某些值,P(x) 为 true。
示例- “有些人不诚实”可以转换为命题形式 $\exists x P(x)$,其中 P(x) 是谓词,表示 x 不诚实,而话语范围是某些人。
嵌套量词
如果我们使用的量词出现在另一个量词的范围内,则称为嵌套量词。
例子
$\forall\ a\: \存在 b\: P (x, y)$ 其中 $P (a, b)$ 表示 $a + b = 0$
$\forall\ a\: \forall\: b\: \forall\: c\: P (a, b, c)$ 其中 $P (a, b)$ 表示 $a + (b + c) = ( a + b) + c$
注意- $\forall\: a\: \exists b\: P (x, y) \ne \exists a\: \forall b\: P (x, y)$
离散数学 - 推理规则
为了从我们已经知道真相的陈述中推导出新的陈述,使用了推理规则。
推理规则有什么用?
数理逻辑经常用于逻辑证明。证明是确定数学陈述真值的有效论据。
参数是一系列陈述。最后一个陈述是结论,其前面的所有陈述称为前提(或假设)。符号“$\therefore$”(读作“therefore”)放在结论之前。有效的论证是根据前提的真值得出结论的论证。
推理规则提供了根据我们已有的陈述构建有效论证的模板或指南。
推理规则表
| 推理规则 | 姓名 | 推理规则 | 姓名 |
|---|---|---|---|
$$\begin{矩阵} P \\ \hline \因此 P \lor Q \end{矩阵}$$ |
添加 |
$$\begin{矩阵} P \lor Q \\ \lnot P \\ \hline \therefore Q \end{矩阵}$$ |
析取三段论 |
$$\begin{矩阵} P \\ Q \\ \hline \therefore P \land Q \end{矩阵}$$ |
连词 |
$$\begin{矩阵} P \rightarrow Q \\ Q \rightarrow R \\ \hline \therefore P \rightarrow R \end{矩阵}$$ |
假设三段论 |
$$\begin{矩阵} P \land Q\\ \hline \因此 P \end{矩阵}$$ |
简化 |
$$\begin{矩阵} ( P \rightarrow Q ) \land (R \rightarrow S) \\ P \lor R \\ \hline \therefore Q \lor S \end{矩阵}$$ |
建设性困境 |
$$\begin{矩阵} P \rightarrow Q \\ P \\ \hline \therefore Q \end{矩阵}$$ |
波南斯作案 |
$$\begin{矩阵} (P \rightarrow Q) \land (R \rightarrow S) \\ \lnot Q \lor \lnot S \\ \hline \therefore \lnot P \lor \lnot R \end{矩阵} $$ |
破坏性困境 |
$$\begin{矩阵} P \rightarrow Q \\ \lnot Q \\ \hline \therefore \lnot P \end{矩阵}$$ |
托伦斯作案 |
添加
如果P是前提,我们可以利用加法法则推导出$P\lorQ$。
$$\begin{矩阵} P \\ \hline \因此 P \lor Q \end{矩阵}$$
例子
设 P 为命题,“他学习非常努力”为真
因此 - “要么他学习非常努力,要么他是一个非常糟糕的学生。” 这里Q是命题“他是一个非常糟糕的学生”。
连词
如果P和Q是两个前提,我们可以使用合取规则来推导$ P \land Q $。
$$\begin{矩阵} P \\ Q \\ \hline \therefore P \land Q \end{矩阵}$$
例子
让P - “他学习非常努力”
让 Q - “他是班上最好的男孩”
因此 - “他学习非常努力,他是班上最好的男孩”
简化
如果$P \land Q$是前提,我们可以使用简化规则来推导P。
$$\begin{矩阵} P \land Q\\ \hline \因此 P \end{矩阵}$$
例子
“他学习很努力,是班上最好的男孩”,$P \land Q$
因此 - “他学习非常努力”
波南斯作案
如果 P 和 $P \rightarrow Q$ 是两个前提,我们可以使用 Modus Ponens 来推导 Q。
$$\begin{矩阵} P \rightarrow Q \\ P \\ \hline \therefore Q \end{矩阵}$$
例子
“如果你有密码,那么你就可以登录facebook”,$P \rightarrow Q$
“你有密码”,P
因此 - “你可以登录 Facebook”
托伦斯作案
如果 $P \rightarrow Q$ 和 $\lnot Q$ 是两个前提,我们可以使用 Modus Tollens 推导 $\lnot P$。
$$\begin{矩阵} P \rightarrow Q \\ \lnot Q \\ \hline \therefore \lnot P \end{矩阵}$$
例子
“如果你有密码,那么你就可以登录facebook”,$P \rightarrow Q$
“您无法登录 Facebook”,$\lnot Q$
因此 - “您没有密码”
析取三段论
如果 $\lnot P$ 和 $P \lor Q$ 是两个前提,我们可以使用析取三段论导出 Q。
$$\begin{矩阵} \lnot P \\ P \lor Q \\ \hline \therefore Q \end{矩阵}$$
例子
“冰淇淋不是香草味的”,$\lnot P$
“冰淇淋要么是香草味的,要么是巧克力味的”,$P \lor Q$
因此 - “冰淇淋是巧克力味的”
假设三段论
如果 $P \rightarrow Q$ 和 $Q \rightarrow R$ 是两个前提,我们可以使用假设三段论推导 $P \rightarrow R$
$$\begin{矩阵} P \rightarrow Q \\ Q \rightarrow R \\ \hline \therefore P \rightarrow R \end{矩阵}$$
例子
“如果下雨,我就不去上学”,$P \rightarrow Q$
“如果我不去学校,我就不需要做作业”,$Q \rightarrow R$
因此 - “如果下雨,我就不需要做作业了”
建设性困境
如果 $( P \rightarrow Q ) \land (R \rightarrow S)$ 和 $P \lor R$ 是两个前提,我们可以使用构造性困境推导 $Q \lor S$。
$$\begin{矩阵} ( P \rightarrow Q ) \land (R \rightarrow S) \\ P \lor R \\ \hline \therefore Q \lor S \end{矩阵}$$
例子
“如果下雨,我就请假”,$( P \rightarrow Q )$
“如果外面很热,我会去洗澡”,$(R \rightarrow S)$
“要么会下雨,要么外面很热”,$P \lor R$
因此 - “我要请假或者去洗澡”
破坏性困境
如果 $(P \rightarrow Q) \land (R \rightarrow S)$ 和 $ \lnot Q \lor \lnot S $ 是两个前提,我们可以利用破坏性困境推导出 $\lnot P \lor \lnot R$。
$$\begin{矩阵} (P \rightarrow Q) \land (R \rightarrow S) \\ \lnot Q \lor \lnot S \\ \hline \therefore \lnot P \lor \lnot R \end{矩阵} $$
例子
“如果下雨,我就请假”,$(P \rightarrow Q )$
“如果外面很热,我会去洗澡”,$(R \rightarrow S)$
“要么我就不请假,要么我就不去洗澡”,$\lnot Q \lor \lnot S$
因此 - “要么不下雨,要么外面不热”
算子与假设
群论是数学和抽象代数的一个分支,它定义了一种名为群的代数结构。一般而言,组由一组元素和对该组上任意两个元素的操作组成,以形成也在该组中的第三个元素。
1854年,英国数学家阿瑟·凯利(Arthur Cayley)首次给出了群的现代定义:
“一组全部不同的符号,并且其中任何两个的乘积(无论以什么顺序),或者其中任何一个的乘积属于该集合,被称为一个群。这些符号通常不可转换[可交换],但具有关联性。”
在本章中,我们将了解构成集合论、群论和布尔代数基础知识的算子和假设。
数学系统中的任何元素集都可以用一组运算符和多个假设来定义。
在一组元素上定义的二元运算符是一种规则,它将该组中的唯一元素分配给每对元素。例如,给定集合 $ A = \lbrace 1, 2, 3, 4, 5 \rbrace $,我们可以说 $\otimes$ 是操作 $c = a \otimes b$ 的二元运算符,如果它指定为 $(a,b)$ 对查找 c 的规则,使得 $a,b,c \in A$。
数学系统的假设构成了可以推导出规则的基本假设。假设是 -
关闭
如果对于集合中的每一对元素,该运算符从该集合中找到唯一的元素,则该集合相对于二元运算符是封闭的。
例子
设 $A = \lbrace 0, 1, 2, 3, 4, 5, \dots \rbrace$
该集合在二元运算符下封闭为 $(\ast)$,因为对于运算 $c = a \ast b$,对于任何 $a, b \in A$,乘积 $c \in A$。
该集合在二元运算符除法 $(\div)$ 下不是封闭的,因为对于运算 $c = a \div b$,对于任何 $a, b \in A$,乘积 c 可能不在集合中答:如果 $a = 7,b = 2$,则 $c = 3.5$。这里$a,b \in A$ 但$c \notin A$。
结合律
当集合 A 上的二元运算符 $\otimes$ 具有以下属性时,它是结合的 -
$(x \otimes y) \otimes z = x \otimes (y \otimes z)$,其中 $x, y, z \in A $
例子
设 $A = \lbrace 1, 2, 3, 4 \rbrace$
运算符加 $( + )$ 是结合律,因为对于 A$ 中的任何三个元素 $x,y,z \,属性 $(x + y) + z = x + ( y + z )$ 成立。
运算符减去 $( - )$ 不具有结合性,因为
$$( x - y ) - z \ne x - ( y - z )$$
交换律
当集合 A 上的二元运算符 $\otimes$ 具有以下属性时,它是可交换的 -
$x \otimes y = y \otimes x$,其中 $x, y \in A$
例子
设 $A = \lbrace 1, 2, 3, 4 \rbrace$
运算符加 $( + )$ 是可交换的,因为对于 A$ 中的任意两个元素 $x,y \,属性 $x + y = y + x$ 成立。
运算符减去 $( - )$ 不具有结合性,因为
$$x - y \ne y - x$$
分配律
当以下属性成立时,集合 A 上的两个二元运算符 $\otimes$ 和 $\circledast$ 在运算符 $\circledast$ 上可分配 -
$x \otimes (y \circledast z) = (x \otimes y) \circledast (x \otimes z)$,其中 $x, y, z \in A $
例子
设 $A = \lbrace 1, 2, 3, 4 \rbrace$
运算符 $( * )$ 和 plus $( + )$ 对运算符 + 具有分配性,因为对于任意三个元素 $x,y,z \in A$,属性 $x * ( y + z ) = ( x * y ) + ( x * z )$ 成立。
然而,这些运算符在 $*$ 上不具有分配性,因为
$$x + ( y * z ) \ne ( x + y ) * ( x + z )$$
单位元
集合 A 对于 A 上的二元运算 $\otimes$ 有一个单位元,如果 A$ 中存在元素 $e \,则以下属性成立 -
$e \otimes x = x \otimes e$,其中 $x \in A$
例子
设 $Z = \lbrace 0, 1, 2, 3, 4, 5, \dots \rbrace$
元素 1 是关于操作 $*$ 的恒等元素,因为对于任何元素 $x \in Z$,
$$1 * x = x * 1$$
另一方面,减去 $( - )$ 的操作没有单位元
逆
如果集合 A 对于二元运算符 $\otimes $ 有一个单位元素 $e$,则只要对于每个元素 $x \in A$,都存在另一个元素 $y \in A$,则称其具有逆元,使得以下属性成立 -
$$x \otimes y = e$$
例子
设 $A = \lbrace \dots -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, \dots \rbrace$
给定运算加上 $( + )$ 和 $e = 0$,任何元素 x 的逆都是 $(-x)$,因为 $x + (x) = 0$
德摩根定律
德摩根定律根据补集给出了两个(或多个)集合的并集和交集之间的一对变换。法律是 -
$$(A \cup B)' = A' \cap B'$$
$$(A \cap B)' = A' \cup B'$$
例子
设 $A = \lbrace 1, 2, 3, 4 \rbrace ,B = \lbrace 1, 3, 5, 7 \rbrace$,并且
通用集 $U = \lbrace 1, 2, 3, \dots, 9, 10 \rbrace$
$A' = \lbrace 5, 6, 7, 8, 9, 10 \rbrace$
$B' = \lbrace 2, 4, 6, 8, 9, 10 \rbrace$
$A \cup B = \lbrace 1, 2, 3, 4, 5, 7 \rbrace$
$A \cap B = \lbrace 1, 3 \rbrace $
$(A \cup B)' = \lbrace 6, 8, 9, 10 \rbrace$
$A' \cap B' = \lbrace 6, 8, 9, 10 \rbrace$
因此,我们看到 $(A \cup B)' = A' \cap B'$
$(A \cap B)' = \lbrace 2, 4, 5, 6, 7, 8, 9, 10 \rbrace$
$A' \cup B' = \lbrace 2, 4, 5, 6, 7, 8, 9, 10 \rbrace$
因此,我们看到 $(A \cap B)' = A' \cup B'$
离散数学-群论
半群
具有二元运算 $'\omicron'$ (组合)的有限或无限集合 $'S'$ 如果同时满足以下两个条件,则称为半群 -
闭包- 对于 S 中的每对 $(a, b) \, \:(a \omicron b)$ 必须出现在集合 $S$ 中。
关联性- 对于 S 中的每个元素 $a, b, c \in,(a \omicron b) \omicron c = a \omicron (b \omicron c)$ 必须成立。
例子
具有加法运算的正整数(不包括零)的集合是半群。例如,$ S = \lbrace 1, 2, 3, \dots \rbrace $
这里,对于每对 $(a, b) \in S,(a + b)$ 都存在于集合 S 中,闭包属性成立。例如, $1 + 2 = 3 \in S]$
关联属性也适用于 S 中的每个元素 $a, b, c,(a + b) + c = a + (b + c)$。例如,$(1 + 2) + 3 = 1 + (2 + 3) = 5$
幺半群
幺半群是具有单位元的半群。集合 S 的单位元素(用 $e$ 或 E 表示)是这样的元素:对于 S$ 中的每个元素 $a \omicron e) = a$。单位元也称为单位元。因此,幺半群同时拥有三个属性:闭包、关联、恒等元素。
例子
具有乘法运算的正整数(不包括零)的集合是幺半群。$S = \lbrace 1, 2, 3, \点 \rbrace $
这里闭包属性对于每对 $(a, b) \in S 来说都成立,(a \times b)$ 存在于集合 S 中。 [例如,$1 \times 2 = 2 \in S$ 等等]
关联属性也适用于 S 中的每个元素 $a, b, c \in S, (a \times b) \times c = a \times (b \times c)$ [例如,$(1 \times 2) \times 3 = 1 \times (2 \times 3) = 6$ 等等]
同一性属性也适用于 S 中的每个元素 $a \times e) = a$ [例如,$(2 \times 1) = 2, (3 \times 1) = 3$ 等等]。这里单位元为1。
团体
群是具有逆元素的幺半群。集合 S 的逆元素(用 I 表示)是这样的元素:对于 S$ 中的每个元素 $a \omicron I) = (I \omicron a) = a$。因此,一个群同时拥有四个属性 - i)闭包,ii)结合,iii)单位元素,iv)逆元素。群 G 的阶是 G 中元素的数量,群中元素的阶是最小正整数 n,使得 an 是该群 G 的单位元素。
例子
$N \times N$ 个非奇异矩阵的集合在矩阵乘法运算下形成一个群。
两个$N \times N$非奇异矩阵的乘积也是一个具有闭包性质的$N \times N$非奇异矩阵。
矩阵乘法本身是结合律的。因此,关联性质成立。
$N \times N$ 非奇异矩阵的集合包含具有单位元素属性的单位矩阵。
由于所有矩阵都是非奇异矩阵,因此它们都具有逆元素,这些元素也是非奇异矩阵。因此,逆性质也成立。
阿贝尔群
阿贝尔群 G 是元素对 $(a,b) \in G$ 始终满足交换律的群。因此,一个群同时拥有五个属性 - i) 闭包,ii) 结合性,iii) 单位元,iv) 逆元,v) 可交换。
例子
具有加法运算的正整数(包括零)的集合是阿贝尔群。$G = \lbrace 0, 1, 2, 3, \点 \rbrace$
这里,对于每对 $(a, b) \in S,(a + b)$ 都存在于集合 S 中,闭包属性成立。 [例如,$1 + 2 = 2 \in S$ 等等]
关联属性也适用于 S 中的每个元素 $a, b, c \in S, (a + b) + c = a + (b + c)$ [例如,$(1 +2) + 3 = 1 + (2 + 3) = 6$ 等等]
同一性属性也适用于 S 中的每个元素 $a \times e) = a$ [例如,$(2 \times 1) = 2, (3 \times 1) = 3$ 等等]。这里,单位元为1。
交换律也适用于 S 中的每个元素 $a \times b) = (b \times a)$ [例如,$(2 \times 3) = (3 \times 2) = 3$ 等等在]
循环群和子群
循环群是可以由单个元素生成的群。循环群的每个元素都是某个特定元素的幂,该元素称为生成元。循环群可以由生成器“g”生成,使得该群的每个其他元素都可以写成生成器“g”的幂。
例子
乘法运算下的复数集合 $\lbrace 1,-1, i, -i \rbrace$ 是一个循环群。
有两个生成器 - $i$ 和 $–i$ 作为 $i^1 = i, i^2 = -1, i^3 = -i, i^4 = 1$ 以及 $(–i)^1 = -i, (–i)^2 = -1, (–i)^3 = i, (–i)^4 = 1$ 覆盖了该组的所有元素。因此,它是一个循环群。
注-循环群始终是阿贝尔群,但并非每个阿贝尔群都是循环群。加法下的有理数不是循环的,而是阿贝尔的。
子群H 是群 G 的子集(用 $H ≤ G$ 表示),如果它同时满足四个属性 -闭包、关联、单位元和逆。
群G中不包含整个群G的子群H称为真子群(记为$H<G$)。循环群的子群是循环的,阿贝尔子群也是阿贝尔的。
例子
设一组 $G = \lbrace 1, i, -1, -i \rbrace$
那么一些子组是 $H_1 = \lbrace 1 \rbrace, H_2 = \lbrace 1,-1 \rbrace$,
这不是子群 − $H_3 = \lbrace 1, i \rbrace$ 因为 $(i)^{-1} = -i$ 不在 $H_3$ 中
偏序集 (POSET)
偏序集合由具有自反、反对称和传递的二元关系的集合组成。“偏序集”缩写为 POSET。
例子
二元运算下小于或等于$(\le)$的实数集合是偏序集。
设集合$S = \lbrace 1, 2, 3 \rbrace$,运算为$\le$
关系为 $\lbrace(1, 1), (2, 2), (3, 3), (1, 2), (1, 3), (2, 3)\rbrace$
该关系 R 自反为 $\lbrace (1, 1), (2, 2), (3, 3)\rbrace \in R$
该关系 R 是反对称的,如
$\lbrace (1, 2), (1, 3), (2, 3) \rbrace \in R\ 和\ \lbrace (1, 2), (1, 3), (2, 3) \rbrace ∉雷亚尔
该关系 R 也是传递性的,如 $\lbrace (1,2), (2,3), (1,3)\rbrace \in R$。
因此,它是一个偏序集。
有向无环图在“可达性”操作下的顶点集是偏序集。
哈斯图
偏序集的哈斯图是有向图,其顶点是偏序集的元素,弧覆盖偏序集中的对 (x, y)。如果在偏序集 $x < y$ 中,则点 x 在哈斯图中显得低于点 y。如果偏序集中 $x<y<z$,则 x 和 z 之间不会显示箭头,因为它是隐式的。
例子
$\lbrace 1, 2, 3 \rbrace = \lbrace \emptyset, \lbrace 1 \rbrace, \lbrace 2 \rbrace, \lbrace 3 \rbrace, \lbrace 1, 2 \rbrace, \lbrace 1 的子集偏序集, 3 \rbrace, \lbrace 2, 3 \rbrace, \lbrace 1, 2, 3 \rbrace \rbrace$ 由以下哈斯图显示 -

线性有序集
线性有序集或全序集是其中每对元素都是可比较的偏序集。如果 $a \le b$ 或 $b \le a$ 成立,则元素 $a, b \in S$ 被认为是可比较的。三分法定义了这个全有序集。全序集可以定义为分布格havin
