晶体管配置
任何晶体管都有三个端子:发射极、基极和集电极。使用这 3 个端子,晶体管可以连接在一个电路中,其中一个端子以三种不同的可能配置为输入和输出共用。
三种类型的配置是公共基极、公共发射极和公共集电极配置。在每种配置中,发射结正向偏置,集电极结反向偏置。
公共底座 (CB) 配置
该名称本身意味着基极端子被视为晶体管输入和输出的公共端子。NPN 和 PNP 晶体管的公共基极连接如下图所示。
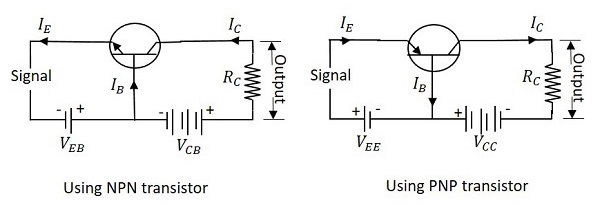
为了便于理解,让我们考虑 CB 配置中的 NPN 晶体管。当施加发射极电压时,由于它是正向偏置,来自负极端子的电子排斥发射极电子,并且电流流经发射极和基极到达集电极以贡献集电极电流。集电极电压V CB在整个过程中保持恒定。
在 CB 配置中,输入电流为发射极电流I E,输出电流为集电极电流I C。
电流放大系数(α)
当集电极电压V CB保持恒定时,集电极电流的变化(ΔI C)与发射极电流的变化(ΔI E )之比称为电流放大系数。它用α表示。
$\alpha = \frac{\Delta I_C}{\Delta I_E}$ 在恒定 V CB下
集电极电流表达式
有了上述想法,让我们尝试画出集电极电流的表达式。
随着发射极电流的流动,还有一定量的基极电流I B由于电子空穴复合而流经基极端子。由于集电极-基极结反向偏置,因此少数电荷载流子会产生另一种电流。这就是漏电流,可以理解为Ileakage。这是由于少数电荷载流子,因此非常小。
到达集电极端子的发射极电流为
$$\alpha I_E$$
总集电极电流
$$I_C = \alpha I_E + I_{泄漏}$$
如果发射极-基极电压V EB = 0,即使如此,也会有小的漏电流流动,这可以称为ICBO (输出开路的集电极-基极电流)。
因此集电极电流可以表示为
$$I_C = \alpha I_E + I_{CBO}$$
$$I_E = I_C + I_B$$
$$I_C = \alpha (I_C + I_B) + I_{CBO}$$
$$I_C (1 - \alpha) = \alpha I_B + I_{CBO}$$
$$I_C = \frac{\alpha}{1 - \alpha}I_B + \frac{I_{CBO}}{1 - \alpha}$$
$$I_C = \left ( \frac{\alpha}{1 - \alpha} \right )I_B + \left ( \frac{1}{1 - \alpha} \right )I_{CBO}$$
因此,上面导出的是集电极电流的表达式。集电极电流的值取决于基极电流和漏电流以及所使用的晶体管的电流放大系数。
CB配置特点
此配置提供电压增益但不提供电流增益。
当V CB恒定时,随着发射极-基极电压V EB的小幅增加,发射极电流I E增加。
发射极电流I E与集电极电压V CB无关。
当V EB保持恒定时,集电极电压V CB仅在低电压下才会影响集电极电流I C 。
输入电阻R i是在集电极基极电压V CB恒定的情况下发射极-基极电压的变化(ΔV EB )与发射极电流的变化(ΔI E )的比率。
$R_i = \frac{\Delta V_{EB}}{\Delta I_E}$ 在恒定 V CB下
由于输入电阻非常低,所以较小的V EB值就足以产生大的发射极电流I E。
输出电阻R o是在发射极电流IE恒定时集电极基极电压的变化(ΔV CB )与集电极电流的变化(ΔI C )的比率。
$R_o = \frac{\Delta V_{CB}}{\Delta I_C}$ 在常数 I E处
由于输出电阻非常高,V CB的较大变化只会导致集电极电流 I C发生很小的变化。
该配置针对温度升高提供了良好的稳定性。
CB 配置用于高频应用。
共发射极 (CE) 配置
该名称本身意味着发射极端子被视为晶体管输入和输出的公共端子。NPN 和 PNP 晶体管的共发射极连接如下图所示。

正如 CB 配置一样,发射结正向偏置,集电极结反向偏置。电子的流动以相同的方式控制。这里输入电流是基极电流I B,输出电流是集电极电流I C 。
基极电流放大系数(β)
集电极电流变化 (ΔI C ) 与基极电流变化 (ΔI B )的比率称为基极电流放大系数。用β表示。
$$\beta = \frac{\Delta I_C}{\Delta I_B}$$
β 和 α 之间的关系
让我们尝试推导出基极电流放大系数和发射极电流放大系数之间的关系。
$$\beta = \frac{\Delta I_C}{\Delta I_B}$$
$$\alpha = \frac{\Delta I_C}{\Delta I_E}$$
$$I_E = I_B + I_C$$
$$\Delta I_E = \Delta I_B + \Delta I_C$$
$$\Delta I_B = \Delta I_E - \Delta I_C$$
我们可以写
$$\beta = \frac{\Delta I_C}{\Delta I_E - \Delta I_C}$$
除以 ΔI E
$$\beta = \frac{\Delta I_C/\Delta I_E}{\frac{\Delta I_E}{\Delta I_E} - \frac{\Delta I_C}{\Delta I_E}}$$
我们有
$$\alpha = \Delta I_C / \Delta I_E$$
所以,
$$\beta = \frac{\alpha}{1 - \alpha}$$
从上式可以明显看出,当α接近1时,β达到无穷大。
因此,共发射极连接的电流增益非常高。这就是这种电路连接主要用于所有晶体管应用的原因。
集电极电流的表达式
在共发射极配置中,I B是输入电流,IC是输出电流。
我们知道
$$I_E = I_B + I_C$$
和
$$I_C = \alpha I_E + I_{CBO}$$
$$= \alpha(I_B + I_C) + I_{CBO}$$
$$I_C(1 - \alpha) = \alpha I_B + I_{CBO}$$
$$I_C = \frac{\alpha}{1 - \alpha}I_B + \frac{1}{1 - \alpha}I_{CBO}$$
如果基极电路开路,即 I B = 0,
基极开路时的集电极发射极电流为 I CEO
$$I_{CEO} = \frac{1}{1 - \alpha}I_{CBO}$$
将其值代入前面的方程中,我们得到
$$I_C = \frac{\alpha}{1 - \alpha}I_B + I_{CEO}$$
$$I_C = \beta I_B + I_{CEO}$$
由此得到集电极电流的方程。
膝点电压
在CE配置中,通过保持基极电流I B恒定,如果V CE变化,IC增加到接近V CE的1v ,并且此后保持恒定。集电极电流 I C随V CE变化的 V CE值称为拐点电压。晶体管在 CE 配置下运行时,它们的运行电压高于该拐点电压。
CE配置的特点
该配置提供良好的电流增益和电压增益。
保持 V CE恒定,随着 V BE的小幅增加,基极电流 I B比 CB 配置中快速增加。
对于任何高于拐点电压的 V CE值,IC约等于βIB。
输入电阻R i是在恒定集电极发射极电压V CE下基极发射极电压变化(ΔV BE )与基极电流变化(ΔI B )之比。
$R_i = \frac{\Delta V_{BE}}{\Delta I_B}$ 在常数 V CE下
由于输入电阻非常低,所以很小的V BE值就足以产生大的基极电流I B。
输出电阻Ro是在 I B恒定时集电极发射极电压变化 (ΔV CE ) 与集电极电流变化 (ΔI C )的比率。
$R_o = \frac{\Delta V_{CE}}{\Delta I_C}$ 恒定 I B
由于CE电路的输出电阻小于CB电路的输出电阻。
这种配置通常用于偏置稳定方法和音频应用。
公共收集器 (CC) 配置
该名称本身意味着集电极端子被视为晶体管输入和输出的公共端子。NPN 和 PNP 晶体管的公共集电极连接如下图所示。

正如 CB 和 CE 配置中一样,发射结正向偏置,集电极结反向偏置。电子的流动以相同的方式控制。这里输入电流是基极电流I B,输出电流是发射极电流I E 。
电流放大系数(γ)
发射极电流变化 (ΔI E ) 与基极电流变化 (ΔI B )的比率称为共集电极 (CC) 配置中的电流放大系数。用γ表示。
$$\gamma = \frac{\Delta I_E}{\Delta I_B}$$
- CC 配置中的电流增益与 CE 配置中的电流增益相同。
- CC 配置中的电压增益始终小于 1。
γ 和 α 之间的关系
让我们尝试画出 γ 和 α 之间的关系
$$\gamma = \frac{\Delta I_E}{\Delta I_B}$$
$$\alpha = \frac{\Delta I_C}{\Delta I_E}$$
$$I_E = I_B + I_C$$
$$\Delta I_E = \Delta I_B + \Delta I_C$$
$$\Delta I_B = \Delta I_E - \Delta I_C$$
代入 I B的值,我们得到
$$\gamma = \frac{\Delta I_E}{\Delta I_E - \Delta I_C}$$
除以 ΔI E
$$\gamma = \frac{\Delta I_E / \Delta I_E}{\frac{\Delta I_E}{\Delta I_E} - \frac{\Delta I_C}{\Delta I_E}}$$
$$= \frac{1}{1 - \alpha}$$
$$\gamma = \frac{1}{1 - \alpha}$$
集电极电流表达式
我们知道
$$I_C = \alpha I_E + I_{CBO}$$
$$I_E = I_B + I_C = I_B + (\alpha I_E + I_{CBO})$$
$$I_E(1 - \alpha) = I_B + I_{CBO}$$
$$I_E = \frac{I_B}{1 - \alpha} + \frac{I_{CBO}}{1 - \alpha}$$
$$I_C \cong I_E = (\beta + 1)I_B + (\beta + 1)I_{CBO}$$
上式是集电极电流的表达式。
CC 配置的特点
此配置提供电流增益但不提供电压增益。
在 CC 配置中,输入电阻较高,输出电阻较低。
该电路提供的电压增益小于1。
集电极电流和基极电流之和等于发射极电流。
输入和输出信号同相。
该配置用作非反相放大器输出。
该电路主要用于阻抗匹配。这意味着,从高阻抗源驱动低阻抗负载。
