摩尔和米利机器
有限自动机可以具有与每个转换相对应的输出。有两种类型的有限状态机生成输出 -
- 打粉机
- 摩尔机
打粉机
Mealy Machine 是一种 FSM,其输出取决于当前状态以及当前输入。
它可以用 6 元组 (Q, Σ, O, δ, X, q 0 )来描述,其中 -
Q是有限状态集。
Σ是一组有限的符号,称为输入字母表。
O是一组有限的符号,称为输出字母表。
δ是输入转换函数,其中 δ: Q × Σ → Q
X是输出转换函数,其中 X: Q × Σ → O
q 0是处理任何输入的初始状态 (q 0 ∈ Q)。
Mealy Machine 的状态表如下所示 -
| 目前状态 | 下一个状态 | |||
|---|---|---|---|---|
| 输入 = 0 | 输入 = 1 | |||
| 状态 | 输出 | 状态 | 输出 | |
| → 一个 | 乙 | x 1 | C | x 1 |
| 乙 | 乙 | x 2 | d | x 3 |
| C | d | x 3 | C | x 1 |
| d | d | x 3 | d | x 2 |
上述 Mealy 机的状态图是 -
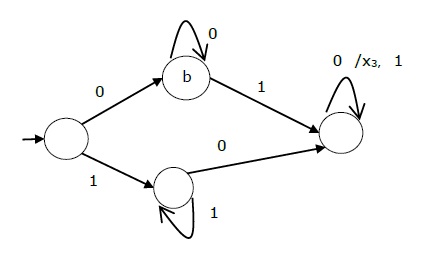
摩尔机
摩尔机是一个 FSM,其输出仅取决于当前状态。
摩尔机可以用 6 元组 (Q, Σ, O, δ, X, q 0 ) 来描述,其中 -
Q是有限状态集。
Σ是一组有限的符号,称为输入字母表。
O是一组有限的符号,称为输出字母表。
δ是输入转换函数,其中 δ: Q × Σ → Q
X是输出转换函数,其中 X: Q → O
q 0是处理任何输入的初始状态 (q 0 ∈ Q)。
摩尔机的状态表如下所示 -
| 目前状态 | 下一个状态 | 输出 | |
|---|---|---|---|
| 输入 = 0 | 输入 = 1 | ||
| → 一个 | 乙 | C | x 2 |
| 乙 | 乙 | d | x 1 |
| C | C | d | x 2 |
| d | d | d | x 3 |
上述摩尔机的状态图是 -
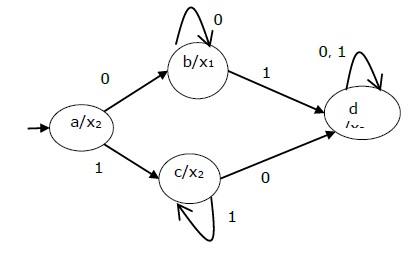
Mealy 机与 Moore 机
下表重点介绍了 Mealy 机器与 Moore 机器的区别点。
| 打粉机 | 摩尔机 |
|---|---|
| 输出取决于当前状态和当前输入 | 输出仅取决于当前状态。 |
| 一般来说,它的状态比摩尔机少。 | 一般来说,它比Mealy Machine有更多的状态。 |
| 当当前状态的输入逻辑完成时,输出函数的值是转换和变化的函数。 | 每当状态发生变化时,输出函数的值是当前状态和时钟边沿变化的函数。 |
| Mealy 机器对输入的反应更快。它们通常在同一时钟周期内做出反应。 | 在摩尔机器中,需要更多的逻辑来解码输出,从而导致更多的电路延迟。它们通常会在一个时钟周期后做出反应。 |
摩尔机到麦利机
算法4
输入- 摩尔机
输出- Mealy 机
步骤 1 - 采用空白 Mealy Machine 转换表格式。
步骤 2 - 将所有摩尔机过渡状态复制到此表格式中。
步骤 3 - 检查摩尔机状态表中的当前状态及其相应的输出;如果状态 Q i 的输出是 m,则将其复制到 Mealy Machine 状态表的输出列中,无论 Q i出现在下一个状态中。
例子
让我们考虑以下摩尔机 -
| 现状 | 下一个状态 | 输出 | |
|---|---|---|---|
| a = 0 | 一个= 1 | ||
| → 一个 | d | 乙 | 1 |
| 乙 | A | d | 0 |
| C | C | C | 0 |
| d | 乙 | A | 1 |
现在我们应用算法 4 将其转换为 Mealy Machine。
步骤 1 和 2 -
| 现状 | 下一个状态 | |||
|---|---|---|---|---|
| a = 0 | 一个= 1 | |||
| 状态 | 输出 | 状态 | 输出 | |
| → 一个 | d | 乙 | ||
| 乙 | A | d | ||
| C | C | C | ||
| d | 乙 | A | ||
步骤 3 -
| 现状 | 下一个状态 | |||
|---|---|---|---|---|
| a = 0 | 一个= 1 | |||
| 状态 | 输出 | 状态 | 输出 | |
| => 一个 | d | 1 | 乙 | 0 |
| 乙 | A | 1 | d | 1 |
| C | C | 0 | C | 0 |
| d | 乙 | 0 | A | 1 |
粉机到摩尔机
算法5
输入- Mealy 机
输出- 摩尔机
步骤 1 - 计算Mealy 机状态表中可用的每个状态 (Q i )的不同输出的数量。
步骤 2 - 如果 Qi 的所有输出都相同,则复制状态 Q i。如果它有 n 个不同的输出,则将 Q i分成 n 个状态,如 Q in其中n = 0, 1, 2.......
步骤 3 - 如果初始状态的输出为 1,则在开头插入一个新的初始状态,该状态给出 0 输出。
例子
让我们考虑以下 Mealy Machine -
| 现状 | 下一个状态 | |||
|---|---|---|---|---|
| a = 0 | 一个= 1 | |||
| 下一个状态 | 输出 | 下一个状态 | 输出 | |
| → 一个 | d | 0 | 乙 | 1 |
| 乙 | A | 1 | d | 0 |
| C | C | 1 | C | 0 |
| d | 乙 | 0 | A | 1 |
这里,状态“a”和“d”分别仅给出 1 和 0 输出,因此我们保留状态“a”和“d”。但状态“b”和“c”产生不同的输出(1 和 0)。因此,我们将b分为b 0、 b 1,将c分为c 0、 c 1。
| 现状 | 下一个状态 | 输出 | |
|---|---|---|---|
| a = 0 | 一个= 1 | ||
| → 一个 | d | 乙1 | 1 |
| 乙0 | A | d | 0 |
| 乙1 | A | d | 1 |
| 0 _ | c 1 | C 0 | 0 |
| c 1 | c 1 | C 0 | 1 |
| d | 乙0 | A | 0 |
