建模与仿真 - 快速指南
建模与仿真 - 简介
建模是表示模型的过程,包括模型的构造和工作。该模型类似于真实的系统,可以帮助分析人员预测系统更改的影响。换句话说,建模是创建一个模型,该模型代表一个系统,包括其属性。这是建立模型的Behave。
系统仿真是模型在时间或空间上的运行,有助于分析现有或拟建系统的性能。换句话说,仿真是使用模型来研究系统性能的过程。它是利用模型进行模拟的Behave。
模拟的历史
模拟的历史视角是按时间顺序列举的。
1940 年- 研究人员(约翰·冯·诺依曼、斯坦尼斯瓦夫·乌兰、爱德华·泰勒、赫尔曼·卡恩)和从事曼哈顿项目研究中子散射的物理学家开发了一种名为“蒙特卡罗”的方法。
1960 - 第一个专用模拟语言被开发出来,例如兰德公司的 Harry Markowitz 开发的 SIMSCRIPT。
1970 – 在此期间,开始了模拟数学基础的研究。
1980 – 在此期间,开发了基于 PC 的仿真软件、图形用户界面和面向对象的编程。
1990 - 在此期间,开发了基于网络的模拟、精美的动画图形、基于模拟的优化、马尔可夫链蒙特卡罗方法。
开发仿真模型
仿真模型由以下部分组成:系统实体、输入变量、性能测量和功能关系。以下是开发仿真模型的步骤。
步骤 1 - 确定现有系统的问题或设定拟议系统的要求。
步骤 2 - 设计问题,同时考虑现有系统因素和限制。
步骤 3 - 收集并开始处理系统数据,观察其性能和结果。
步骤 4 - 使用网络图开发模型并使用各种验证技术对其进行验证。
步骤 5 - 通过将各种条件下的性能与真实系统进行比较来验证模型。
步骤 6 - 创建模型文档以供将来使用,其中详细包括目标、假设、输入变量和性能。
步骤 7 - 根据要求选择适当的实验设计。
步骤 8 - 在模型上引入实验条件并观察结果。
进行模拟分析
以下是执行模拟分析的步骤。
步骤 1 - 准备问题陈述。
步骤 2 - 选择输入变量并为模拟过程创建实体。变量有两种类型——决策变量和不可控变量。决策变量是由程序员控制的,而不可控变量是随机变量。
步骤 3 - 通过将决策变量分配给模拟过程来创建对决策变量的约束。
步骤 4 - 确定输出变量。
步骤 5 - 从现实系统收集数据以输入到模拟中。
步骤 6 - 制定流程图,显示模拟过程的进度。
步骤 7 - 选择合适的模拟软件来运行模型。
步骤 8 - 通过将仿真模型的结果与实时系统进行比较来验证仿真模型。
步骤 9 - 通过更改变量值对模型进行实验以找到最佳解决方案。
步骤 10 - 最后,将这些结果应用到实时系统中。
建模与仿真 ─ 优点
以下是使用建模和仿真的优点 -
易于理解- 无需在实时系统上工作即可了解系统的实际运行方式。
易于测试- 允许对系统进行更改及其对输出的影响,而无需在实时系统上工作。
易于升级- 允许通过应用不同的配置来确定系统要求。
易于识别约束- 允许执行导致工作流程、信息等延迟的瓶颈分析。
易于诊断问题- 某些系统非常复杂,很难一次理解它们的交互。然而,建模和仿真可以理解所有的相互作用并分析它们的效果。此外,可以在不影响实际系统的情况下探索新的策略、操作和程序。
建模与仿真 ─ 缺点
以下是使用建模和仿真的缺点 -
设计模型是一门艺术,需要领域知识、培训和经验。
系统使用随机数进行运算,因此很难预测结果。
模拟需要人力,而且是一个耗时的过程。
模拟结果很难转化。需要专家才能理解。
模拟过程是昂贵的。
建模与仿真 ─ 应用领域
建模和仿真可应用于以下领域:军事应用、培训和支持、半导体设计、电信、土木工程设计和演示以及电子商务模型。
此外,它还用于研究复杂系统(例如生物系统)的内部结构。它在优化系统设计(例如路由算法、装配线等)时使用。它用于测试新的设计和策略。它用于验证解析解。
概念与分类
在本章中,我们将讨论建模的各种概念和分类。
模型与活动
以下是建模与仿真的基本概念。
对象是存在于现实世界中用于研究模型Behave的实体。
基本模型是对对象属性及其Behave的假设解释,在整个模型中都有效。
系统是现实世界中存在的、在一定条件下的清晰的对象。
实验框架用于研究现实世界中的系统,例如实验条件、方面、目标等。基本实验框架由两组变量组成 - 框架输入变量和框架输出变量,与系统或模型相匹配终端。Frame 输入变量负责匹配应用于系统或模型的输入。框架输出变量负责将输出值与系统或模型进行匹配。
集总模型是对遵循给定实验框架的指定条件的系统的精确解释。
验证是比较两个或多个项目以确保其准确性的过程。在建模与仿真中,可以通过比较仿真程序与集总模型的一致性来进行验证,以确保其性能。执行验证过程的方法有多种,我们将在单独的章节中介绍。
验证是比较两个结果的过程。在建模和仿真中,通过将实验测量值与实验框架内的仿真结果进行比较来执行验证。如果结果不匹配,则模型无效。执行验证过程的方法有多种,我们将在单独的章节中介绍。
系统状态变量
系统状态变量是定义给定时间点系统内部过程所需的一组数据。
在离散事件模型中,系统状态变量在一段时间内保持恒定,并且值在称为事件时间的定义点发生变化。
在连续事件模型中,系统状态变量由微分方程结果定义,其值随时间连续变化。
以下是一些系统状态变量 -
实体和属性- 实体表示一个对象,其值可以是静态的或动态的,具体取决于与其他实体的过程。属性是实体使用的本地值。
资源- 资源是一次为一个或多个动态实体提供服务的实体。动态实体可以请求一个或多个单位的资源;如果接受,则该实体可以使用该资源并在完成后释放。如果被拒绝,实体可以加入队列。
列表- 列表用于表示实体和资源使用的队列。根据进程的不同,队列有多种可能性,例如 LIFO、FIFO 等。
延迟- 这是由系统条件的某种组合引起的不确定的持续时间。
型号分类
系统可以分为以下几类。
离散事件仿真模型- 在该模型中,状态变量值仅在事件发生的某些离散时间点发生变化。事件只会在定义的活动时间和延迟发生。
随机与确定性系统- 随机系统不受随机性影响,其输出不是随机变量,而确定性系统受随机性影响,其输出是随机变量。
静态与动态模拟- 静态模拟包括不随时间影响的模型。例如:蒙特卡罗模型。动态仿真包括受时间影响的模型。
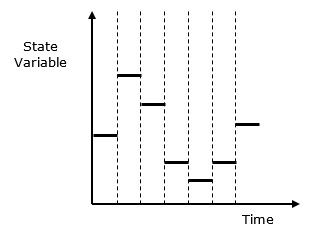
离散系统与连续系统- 离散系统受离散时间点状态变量变化的影响。其Behave如下图所示。
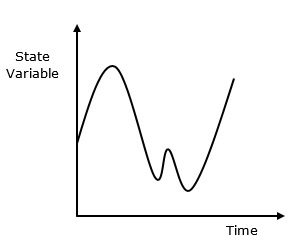
连续系统受状态变量的影响,状态变量随时间连续变化。其Behave如下图所示。
建模过程
建模过程包括以下步骤。
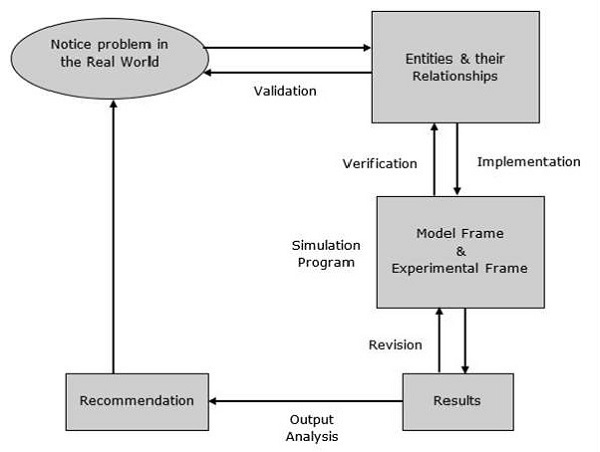
步骤 1 - 检查问题。在这个阶段,我们必须了解问题并相应地选择其分类,例如确定性或随机性。
步骤 2 - 设计模型。在这个阶段,我们必须执行以下简单的任务来帮助我们设计模型 -
根据系统Behave和未来需求收集数据。
分析系统特征、其假设以及为使模型成功而需要采取的必要措施。
确定模型中使用的变量名称、函数、其单位、关系及其应用。
使用合适的技术求解模型并使用验证方法验证结果。接下来,验证结果。
准备一份报告,其中包括结果、解释、结论和建议。
步骤 3 - 完成与模型相关的整个过程后提供建议。包括投资、资源、算法、技术等。
验证与确认
仿真分析师面临的实际问题之一是验证模型。仿真模型只有在模型能够准确表示实际系统时才有效,否则无效。
验证和验证是任何仿真项目中验证模型的两个步骤。
验证是比较两个结果的过程。在此过程中,我们需要将概念模型的表示与真实系统进行比较。如果比较为真,则有效,否则无效。
验证是比较两个或多个结果以确保其准确性的过程。在此过程中,我们必须将模型的实现及其相关数据与开发人员的概念描述和规范进行比较。
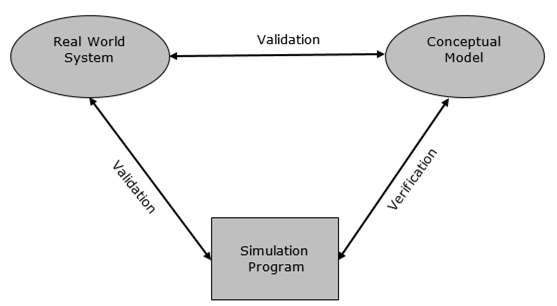
验证和确认技术
有多种技术可用于执行仿真模型的验证和确认。以下是一些常见技术 -
仿真模型验证技术
以下是执行仿真模型验证的方法 -
通过运用编程技巧,在子程序中编写和调试程序。
通过使用“结构化走查”政策,其中不止一个人阅读该程序。
通过追踪中间结果并将其与观察到的结果进行比较。
通过使用各种输入组合检查仿真模型输出。
通过将最终模拟结果与分析结果进行比较。
验证仿真模型的技术
步骤 1 - 设计一个具有高有效性的模型。这可以通过以下步骤来实现 -
- 设计时必须与系统专家讨论模型。
- 模型必须在整个过程中与客户交互。
- 输出必须由系统专家监督。
步骤 2 - 在假设数据上测试模型。这可以通过将假设数据应用到模型中并对其进行定量测试来实现。当输入数据发生重大变化时,还可以进行敏感分析以观察结果变化的影响。
步骤 3 - 确定模拟模型的代表性输出。这可以通过以下步骤来实现 -
确定仿真输出与真实系统输出的接近程度。
可以使用图灵测试进行比较。它以系统格式呈现数据,只有专家才能解释。
可以使用统计方法将模型输出与实际系统输出进行比较。
模型数据与真实数据对比
模型开发完成后,我们必须将其输出数据与真实系统数据进行比较。以下是执行此比较的两种方法。
验证现有系统
在这种方法中,我们使用模型的真实世界输入将其输出与真实系统的真实输入进行比较。这个验证过程很简单,但是在执行时可能会遇到一些困难,例如如果要将输出与平均长度、等待时间、空闲时间等进行比较,则可以使用统计检验和假设检验进行比较。一些统计检验包括卡方检验、Kolmogorov-Smirnov 检验、Cramer-von Mises 检验和 Moments 检验。
验证首次模型
考虑到我们必须描述一个当前不存在也不在过去存在的提议系统。因此,没有可用的历史数据来比较其性能。因此,我们必须使用基于假设的假设系统。遵循有用的指导将有助于提高效率。
子系统有效性- 模型本身可能没有任何现有系统可以与之比较,但它可能由已知的子系统组成。每个有效性都可以单独测试。
内部有效性- 具有高度内部方差的模型将被拒绝,因为由于其内部过程而具有高方差的随机系统将隐藏由于输入变化而导致的输出变化。
敏感性分析- 它提供了我们需要高度关注的系统中敏感参数的信息。
表面有效性- 当模型执行相反的逻辑时,即使它的Behave像真实系统,也应该被拒绝。
离散系统仿真
在离散系统中,系统状态的变化是不连续的,系统状态的每次变化称为事件。离散系统仿真中使用的模型有一组数字来表示系统的状态,称为状态描述符。在本章中,我们还将学习排队仿真,这与分时系统仿真一样,是离散事件仿真中非常重要的一个方面。
以下是离散系统仿真Behave的图形表示。
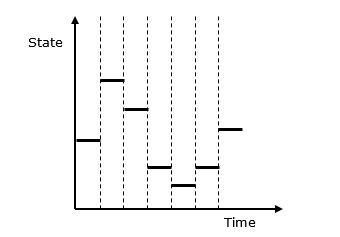
离散事件模拟 ─ 主要特点
离散事件模拟通常由用高级编程语言(例如Pascal、C++或任何专用模拟语言)设计的软件来执行。以下是五个主要特征 -
实体- 这些是真实元素的表示,例如机器的零件。
关系- 意味着将实体链接在一起。
模拟执行器- 负责控制提前时间并执行离散事件。
随机数生成器- 它有助于模拟进入模拟模型的不同数据。
结果和统计- 它验证模型并提供其性能指标。
时间图表示
每个系统都取决于一个时间参数。在图形表示中,它被称为时钟时间或计时器,最初它被设置为零。时间根据以下两个因素更新 -
时间切片- 模型为每个事件定义的时间,直到没有任何事件为止。
下一个事件- 它是由模型定义的事件,用于执行下一个事件而不是时间间隔。它比时间切片更有效率。
排队系统的模拟
队列是系统中正在服务的所有实体和等待轮到的实体的组合。
参数
以下是排队系统中使用的参数列表。
| 象征 | 描述 |
|---|---|
| λ | 表示到达率,即每秒到达的数量 |
| TS | 表示每次到达的平均服务时间,不包括排队等待时间 |
| σTs | 表示服务时间的标准差 |
| ρ | 表示服务器时间利用率,包括空闲和繁忙时 |
| 你 | 表示交通强度 |
| r | 表示系统中项目的平均值 |
| 右 | 表示系统中的项目总数 |
| Tr | 表示系统中某个项目的平均时间 |
| TR | 表示某项在系统中的总时间 |
| σr | 表示 r 的标准差 |
| σTr | 表示 Tr 的标准差 |
| w | 表示队列中等待的平均项目数 |
| σw | 表示 w 的标准差 |
| 特瓦 | 表示所有商品的平均等待时间 |
| TD | 表示队列中等待的项目的平均等待时间 |
| 氮 | 表示系统中服务器的数量 |
| MX(Y) | 表示第 y个百分位数,表示 y 的值,低于该值 x 出现的时间百分比为 y |
单服务器队列
这是最简单的排队系统,如下图所示。系统的核心元件是服务器,它为连接的设备或项目提供服务。如果服务器空闲,则向系统请求提供服务的项目。然后,立即提供服务,否则它会加入等待队列。服务器完成任务后,物品离开。
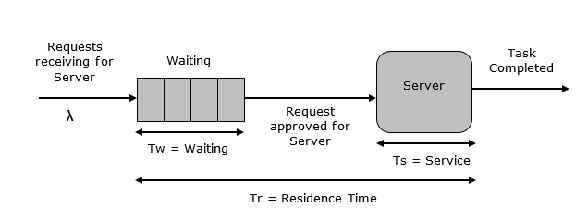
多服务器队列
顾名思义,该系统由多个服务器和所有项目的公共队列组成。当任何项目请求服务器时,如果至少有一个服务器可用,则会分配该项目。否则队列开始启动,直到服务器空闲为止。在这个系统中,我们假设所有服务器都是相同的,即为哪个项目选择哪个服务器没有区别。
使用上有一个例外。令N为相同的服务器,则ρ为每台服务器的利用率。考虑Nρ为整个系统的利用率;则最大利用率为N*100%,最大输入率为 -
$λmax = \frac{\text{N}}{\text{T}s}$
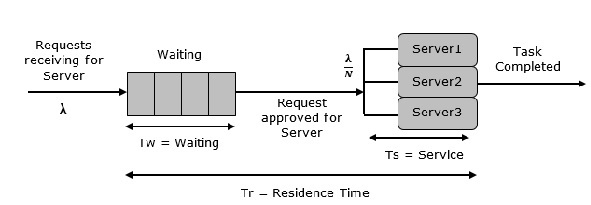
排队关系
下表显示了一些基本的排队关系。
| 一般条款 | 单服务器 | 多服务器 |
|---|---|---|
| r = λTr 利特尔公式 | ρ = λTs | ρ = λTs/N |
| w = λTw 利特尔公式 | r = w + ρ | u = λTs = ρN |
| Tr = Tw + Ts | r = w + Nρ |
分时系统仿真
分时系统的设计方式是每个用户使用系统上共享的一小部分时间,从而导致多个用户同时共享系统。每个用户的切换如此之快,以至于每个用户都感觉像是在使用自己的系统。它基于 CPU 调度和多道编程的概念,通过在系统上同时执行多个作业,可以有效地利用多个资源。
示例- SimOS 仿真系统。
它由斯坦福大学设计,用于研究复杂的计算机硬件设计、分析应用程序性能以及研究操作系统。SimOS 包含现代计算机系统所有硬件组件的软件模拟,即处理器、内存管理单元 (MMU)、缓存等。
建模与仿真 - 连续
连续系统是指系统的重要活动顺利完成,没有任何延迟,即没有事件队列,没有时间模拟排序等。当对连续系统进行数学建模时,代表属性的变量由连续函数控制。
什么是连续模拟?
连续仿真是一种状态变量随时间连续变化的仿真。以下是其Behave的图形表示。
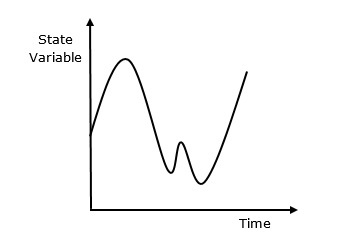
为什么要使用连续仿真?
我们必须使用连续模拟,因为它取决于与系统相关的各种参数的微分方程以及我们已知的估计结果。
应用领域
连续模拟用于以下领域。在土木工程中用于修建堤坝和隧道建设。在军事应用中,用于导弹弹道仿真、战斗机训练仿真、水下航行器智能控制器的设计与测试。
在收费广场设计、机场航站楼客流分析以及主动航班时刻评估等物流方面。在业务发展中进行产品开发规划、人员管理规划、市场研究分析。
蒙特卡罗模拟
蒙特卡罗模拟是一种计算机数学技术,用于根据数值实验的一些已知分布生成随机样本数据。该方法应用于风险定量分析和决策问题。该方法被金融、项目管理、能源、制造、工程、研发、保险、石油和天然气、运输等各种专业人士使用。
这种方法最早是在1940年由研究Atomics弹的科学家使用的。这种方法可以用在那些我们需要做出估计和不确定决策的情况,例如天气预报。
蒙特卡罗模拟 ─ 重要特征
以下是蒙特卡罗方法的三个重要特征 -
- 其输出必须生成随机样本。
- 必须知道其输入分布。
- 在进行实验时必须知道其结果。
蒙特卡罗模拟 ─ 优点
- 易于实施。
- 使用计算机为数值实验提供统计采样。
- 提供数学问题的近似解。
- 可用于随机和确定性问题。
蒙特卡罗模拟 ─ 缺点
耗时,因为需要生成大量采样才能获得所需的输出。
该方法的结果只是真实值的近似值,而不是精确值。
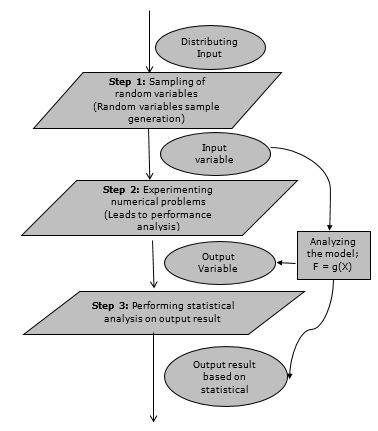
蒙特卡洛模拟法─流程图
下图显示了蒙特卡罗模拟的一般流程图。
建模与仿真 - 数据库
建模与仿真中数据库的目标是提供数据表示及其关系以用于分析和测试目的。第一个数据模型由 Edgar Codd 于 1980 年提出。以下是该模型的显着特征。
数据库是定义信息及其关系的不同数据对象的集合。
规则用于定义对象中数据的约束。
可以将操作应用于对象以检索信息。
最初,数据建模基于实体和关系的概念,其中实体是数据的信息类型,关系表示实体之间的关联。
数据建模的最新概念是面向对象的设计,其中实体表示为类,在计算机编程中用作模板。具有名称、属性、约束以及与其他类的对象的关系的类。
它的基本表示如下 -
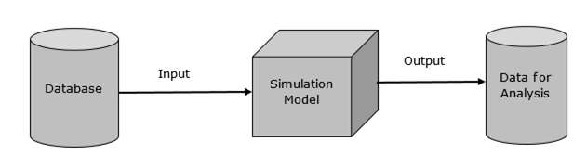
数据表示
事件的数据表示
模拟事件具有其属性,例如事件名称及其关联的时间信息。它表示使用与输入文件参数关联的一组输入数据来执行所提供的模拟,并将其结果提供为一组输出数据,存储在与数据文件关联的多个文件中。
输入文件的数据表示
每个仿真过程都需要一组不同的输入数据及其关联的参数值,这些数据在输入数据文件中表示。输入文件与处理模拟的软件相关联。数据模型通过与数据文件的关联来表示引用的文件。
输出文件的数据表示
当仿真过程完成时,它会产生各种输出文件,每个输出文件都表示为一个数据文件。每个文件都有其名称、描述和通用因素。一个数据文件分为两个文件。第一个文件包含数值,第二个文件包含数字文件内容的描述信息。
建模与仿真中的神经网络
神经网络是人工智能的一个分支。神经网络是由许多称为单元的处理器组成的网络,每个单元都有其小的本地存储器。每个单元通过称为连接的单向通信通道连接,这些通道携带数字数据。每个单元仅处理其本地数据和从连接接收的输入。
历史
模拟的历史视角是按时间顺序列举的。
第一个神经模型由 McCulloch & Pitts于1940 年开发。
1949年,唐纳德·赫布(Donald Hebb)写了一本《Behave的组织》一书,其中指出了神经元的概念。
1950年,随着计算机的进步,根据这些理论建立模型成为可能。它是由 IBM 研究实验室完成的。然而,这一努力失败了,后来的尝试也取得了成功。
1959年,Bernard Widrow和Marcian Hoff开发了名为ADALINE和MADALINE的型号。这些模型具有多个自适应线性元件。MADALINE 是第一个应用于现实世界问题的神经网络。
1962年,Rosenblatt开发了感知器模型,具有解决简单模式分类问题的能力。
1969年,Minsky 和 Papert 提供了感知器模型在计算中的局限性的数学证明。据说感知器模型无法解决异或问题。这些缺点导致神经网络暂时衰落。
1982 年,加州理工学院的约翰·霍普菲尔德 (John Hopfield) 在纸上向美国国家科学院提出了他的想法,即使用双向线制造机器。以前,使用的是单向线路。
当涉及符号方法的传统人工智能技术失败时,就需要使用神经网络。神经网络拥有大规模并行技术,可以提供解决此类问题所需的计算能力。
应用领域
神经网络可用于语音合成机、模式识别、检测诊断问题、机器人控制板和医疗设备。
建模与仿真中的模糊集
如前所述,连续模拟的每个过程都取决于微分方程及其参数,例如 a、b、c、d > 0。通常,在模型中计算和使用点估计。然而,有时这些估计是不确定的,因此我们需要微分方程中的模糊数,它提供未知参数的估计。
什么是模糊集?
在经典集合中,元素要么是集合的成员,要么不是。模糊集根据经典集X定义为 -
A = {(x,μA(x))| x ∈ X}
情况 1 - 函数μA(x)具有以下属性 -
∀x ∈ X μA(x) ≥ 0
sup x ∈ X {μA(x)} = 1
情况 2 - 令模糊集B定义为A = {(3, 0.3), (4, 0.7), (5, 1), (6, 0.4)} ,则其标准模糊符号写为A = {0.3 /3, 0.7/4, 1/5, 0.4/6}
任何成员资格等级为零的值都不会出现在集合的表达式中。
案例 3 - 模糊集和经典清晰集之间的关系。
下图描述了模糊集和经典清晰集之间的关系。