图算法

---

图是一种抽象符号，用于表示对象对之间的连接。图表包括 -

• 顶点- 图中互连的对象称为顶点。顶点也称为节点。

• 边- 边是连接顶点的链接。

有两种类型的图表 -

• 有向图- 在有向图中，边有方向，即边从一个顶点到另一个顶点。

• 无向图- 在无向图中，边没有方向。

图形着色

图着色是一种为图的顶点分配颜色的方法，这样相邻的两个顶点就不会具有相同的颜色。一些图形着色问题是 -

• 顶点着色- 一种对图的顶点进行着色的方法，以便没有两个相邻顶点共享相同的颜色。

• 边缘着色- 这是为每个边缘分配颜色的方法，以便没有两个相邻边缘具有相同的颜色。

• 面着色- 它将颜色分配给平面图的每个面或区域，以便共享公共边界的两个面不会具有相同的颜色。

色数

色数是为图形着色所需的最小颜色数。例如，下图的色数为3。

图形着色的概念应用于准备时间表、移动射频分配、数独、寄存器分配和地图着色。

图形着色的步骤

• 将n维数组中每个处理器的初始值设置为1。

• 现在，要将特定颜色分配给顶点，请确定该颜色是否已分配给相邻顶点。

• 如果处理器在相邻顶点中检测到相同的颜色，则会将其在数组中的值设置为 0。

• 进行n ²次比较后，如果数组中有任何元素为1，则它是有效的着色。

图形着色的伪代码

begin

   create the processors P(i0,i1,...in-1) where 0_iv < m, 0 _ v < n
   status[i0,..in-1] = 1
	
   for j varies from 0 to n-1 do
      begin
		
         for k varies from 0 to n-1 do
         begin
            if aj,k=1 and ij=ikthen
            status[i0,..in-1] =0
         end
			
      end
      ok = ΣStatus
		
   if ok > 0, then display valid coloring exists
   else
      display invalid coloring
      
end

最小生成树

其所有边的权重（或长度）总和小于图 G 的所有其他可能的生成树的生成树称为最小生成树或最小成本生成树。下图显示了一个加权连通图。

上图的一些可能的生成树如下所示 -

在上述所有生成树中，图(d)是最小生成树。最小成本生成树的概念应用于旅行商问题、设计电子电路、设计高效网络和设计高效路由算法。

为了实现最小成本生成树，使用以下两种方法 -

• 普里姆算法
• 克鲁斯卡尔算法

普里姆算法

Prim的算法是一种贪心算法，它帮助我们找到带权无向图的最小生成树。它首先选择一个顶点，并找到该顶点上具有最低权重的边。

Prim算法的步骤

• 选择任意顶点，例如图 G 的v _{1 。}

• 选择一条边，例如 G 的 e ₁，使得 e ₁ = v ₁ v ₂且 v ₁ ≠ v ₂并且 e ₁在图 G 中与 v ₁相关的边中具有最小权重。

• _{现在，按照步骤 2，选择入射到 v 2}上的最小加权边。

• 继续此操作，直到选择了 n–1 条边。这里n是顶点的数量。

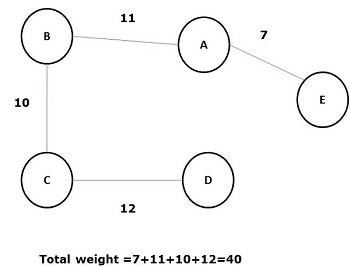
最小生成树是 -

克鲁斯卡尔算法

Kruskal 算法是一种贪心算法，它可以帮助我们找到连通加权图的最小生成树，并在每一步添加递增的成本弧。它是一种最小生成树算法，可找到连接森林中任意两棵树的最小可能权重边。

克鲁斯卡尔算法的步骤

• 选择权重最小的边；假设图 G 的e _{1且 e 1}不是循环。

• _{选择连接到 e 1}的下一个最小加权边。

• 继续此操作，直到选择了 n–1 条边。这里n是顶点的数量。

上图的最小生成树是 -

最短路径算法

最短路径算法是一种寻找从源节点（S）到目的节点（D）的最小成本路径的方法。在这里，我们将讨论摩尔算法，也称为广度优先搜索算法。

摩尔算法

• 标记源顶点 S 并将其标记为i并设置i=0。

• 查找与标记为i 的顶点相邻的所有未标记顶点。如果没有顶点连接到顶点 S，则顶点 D 不会连接到 S。如果有顶点连接到 S，则将它们标记为i+1。

• 如果D被标记，则转到步骤4，否则转到步骤2以增加i=i+1。

• 找到最短路径的长度后停止。