
- Parallel Algorithm Tutorial
- Parallel Algorithm Home
- Parallel Algorithm Introduction
- Parallel Algorithm Analysis
- Parallel Algorithm Models
- Parallel Random Access Machines
- Parallel Algorithm Structure
- Design Techniques
- Matrix Multiplication
- Parallel Algorithm - Sorting
- Parallel Search Algorithm
- Graph Algorithm
- Parallel Algorithm Useful Resources
- Parallel Algorithm - Quick Guide
- Parallel Algorithm - Useful Resources
- Parallel Algorithm - Discussion
并行算法 - 快速指南
并行算法 - 简介
算法是一系列步骤,从用户处获取输入并经过一些计算后产生输出。并行算法是一种可以在不同处理设备上同时执行多个指令,然后组合所有单独输出以产生最终结果的算法。
并发处理
计算机的便捷使用以及互联网的发展改变了我们存储和处理数据的方式。我们生活在一个数据丰富的时代。我们每天都会处理大量数据,这些数据需要复杂的计算,而且速度也很快。有时,我们需要从同时发生的相似或相关事件中获取数据。这就是我们需要并发处理的地方,它可以划分复杂的任务并在多个系统上处理它以快速产生输出。
当任务涉及处理大量复杂数据时,并发处理至关重要。例子包括 - 访问大型数据库、飞机测试、天文计算、Atomics和核物理、生物医学分析、经济规划、图像处理、机器人、天气预报、基于网络的服务等。
什么是并行性?
并行是同时处理多组指令的过程。它减少了总计算时间。并行性可以通过使用并行计算机(即具有许多处理器的计算机)来实现。并行计算机需要支持多任务处理的并行算法、编程语言、编译器和操作系统。
在本教程中,我们将仅讨论并行算法。在进一步讨论之前,让我们首先讨论算法及其类型。
什么是算法?
算法是解决问题所遵循的一系列指令。在设计算法时,我们应该考虑执行算法的计算机的体系结构。根据架构,有两种类型的计算机 -
- 顺序计算机
- 并行计算机
根据计算机的体系结构,我们有两种类型的算法 -
顺序算法- 一种算法,其中按时间顺序执行一些连续的指令步骤来解决问题。
并行算法- 问题被分为子问题并并行执行以获得单独的输出。随后,将这些单独的输出组合在一起以获得最终所需的输出。
将一个大问题分解为子问题并不容易。子问题之间可能存在数据依赖性。因此,处理器必须相互通信来解决问题。
已经发现处理器相互通信所需的时间比实际处理时间要多。因此,在设计并行算法时,应考虑适当的CPU利用率以获得高效的算法。
为了正确地设计算法,我们必须清楚地了解并行计算机中计算的基本模型。
计算模型
顺序计算机和并行计算机都在称为算法的指令集(流)上运行。这些指令(算法)指示计算机在每个步骤中必须做什么。
根据指令流和数据流,计算机可以分为四类 -
- 单指令流、单数据流 (SISD) 计算机
- 单指令流、多数据流 (SIMD) 计算机
- 多指令流、单数据流 (MISD) 计算机
- 多指令流、多数据流 (MIMD) 计算机
SISD计算机
SISD计算机包含1个控制单元、1个处理单元和1个存储单元。

在这种类型的计算机中,处理器从控制单元接收单个指令流并对来自存储器单元的单个数据流进行操作。在计算期间,在每一步,处理器从控制单元接收一条指令并对从存储单元接收的单个数据进行操作。
SIMD计算机
SIMD计算机包含一个控制单元、多个处理单元以及共享存储器或互连网络。

在这里,一个控制单元向所有处理单元发送指令。在计算期间,在每个步骤中,所有处理器从控制单元接收单个指令集,并对来自存储单元的不同数据集进行操作。
每个处理单元都有自己的本地存储单元来存储数据和指令。在 SIMD 计算机中,处理器之间需要进行通信。这是通过共享内存或互连网络来完成的。
当一些处理器执行一组指令时,其余处理器等待它们的下一组指令。来自控制单元的指令决定哪个处理器将处于活动状态(执行指令)或处于非活动状态(等待下一条指令)。
MISD计算机
顾名思义,MISD计算机包含多个控制单元、多个处理单元和一个公共存储单元。

在这里,每个处理器都有自己的控制单元,并且共享一个公共内存单元。所有处理器分别从它们自己的控制单元获取指令,并且它们根据从各自控制单元接收到的指令对单个数据流进行操作。该处理器同时运行。
MIMD计算机
MIMD计算机具有多个控制单元、多个处理单元以及共享存储器或互连网络。
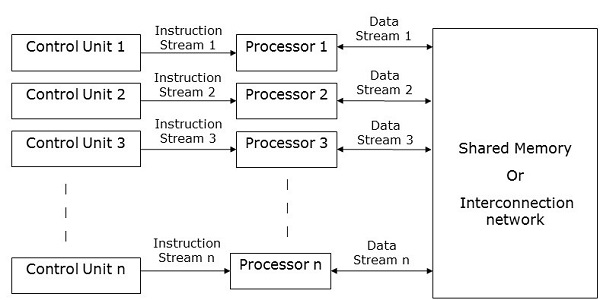
这里,每个处理器都有自己的控制单元、本地存储单元和算术逻辑单元。它们从各自的控制单元接收不同的指令集并对不同的数据集进行操作。
笔记
共享公共内存的 MIMD 计算机称为多处理器,而使用互连网络的计算机称为多计算机。
根据处理器的物理距离,多计算机有两种类型 -
多计算机- 当所有处理器彼此非常接近时(例如,在同一房间中)。
分布式系统- 当所有处理器彼此相距很远时(例如,在不同的城市)
并行算法-分析
对算法的分析可以帮助我们确定该算法是否有用。通常,根据算法的执行时间(时间复杂度)和所需的空间量(空间复杂度)来分析算法。
由于我们以合理的成本提供先进的存储设备,因此存储空间不再是问题。因此,空间复杂度并没有那么重要。
并行算法旨在提高计算机的计算速度。为了分析并行算法,我们通常考虑以下参数 -
- 时间复杂度(执行时间),
- 使用的处理器总数,以及
- 总成本。
时间复杂度
开发并行算法的主要原因是为了减少算法的计算时间。因此,评估算法的执行时间对于分析其效率极其重要。
执行时间是根据算法解决问题所花费的时间来衡量的。总执行时间是从算法开始执行到停止的时刻计算的。如果所有处理器不同时开始或结束执行,则算法的总执行时间是第一个处理器开始执行的时刻到最后一个处理器停止执行的时刻。
算法的时间复杂度可以分为三类 -
最坏情况复杂度- 当给定输入的算法所需的时间量最大时。
平均情况复杂度- 当给定输入的算法所需的时间量为平均时。
最佳情况复杂度- 当给定输入的算法所需的时间最小时。
渐近分析
算法的复杂性或效率是算法为获得所需输出而执行的步骤数。渐近分析是为了计算算法在理论分析中的复杂度。在渐近分析中,使用大长度的输入来计算算法的复杂度函数。
注意-渐近是直线趋于与曲线相交但它们不相交的情况。这里直线和曲线彼此渐近。
渐近符号是描述使用速度上限和下限的算法的最快和最慢可能执行时间的最简单方法。为此,我们使用以下符号 -
- 大O表示法
- 欧米茄表示法
- 西塔符号
大O表示法
在数学中,大O表示法用于表示函数的渐近特征。它以简单而准确的方法表示大输入时函数的Behave。它是一种表示算法执行时间上限的方法。它表示算法完成其执行所需的最长时间。该函数 -
f(n) = O(g(n))
当且仅当存在正常数c和n 0,使得对于所有n,其中n ≥ n 0, f(n) ≤ c * g(n)。
欧米茄表示法
欧米茄表示法是一种表示算法执行时间下限的方法。该函数 -
f(n) = Ω (g(n))
当且仅当存在正常数c和n 0,使得对于所有n,其中n ≥ n 0, f(n) ≥ c * g(n)。
西塔表示法
Theta 表示法是一种表示算法执行时间的下限和上限的方法。该函数 -
f(n) = θ(g(n))
当且仅当存在正常数c 1、 c 2和n 0,使得对于所有n(其中n ≥ n 0 ),c1 * g(n) ≤ f(n) ≤ c2 * g (n) 。
算法加速
并行算法的性能是通过计算其加速比来确定的。加速比定义为针对特定问题的已知最快顺序算法的最坏情况执行时间与并行算法的最坏情况执行时间之比。
使用的处理器数量
使用的处理器数量是分析并行算法效率的重要因素。计算购买、维护和运行计算机的成本。算法解决问题所使用的处理器数量越多,获得的结果的成本就越高。
总成本
并行算法的总成本是时间复杂度和该特定算法中使用的处理器数量的乘积。
总成本 = 时间复杂度 × 使用的处理器数量
因此,并行算法的效率是 -
并行算法 - 模型
并行算法的模型是通过考虑划分数据的策略和处理方法并应用合适的策略来减少交互而开发的。在本章中,我们将讨论以下并行算法模型 -
- 数据并行模型
- 任务图模型
- 工作池模型
- 主从模型
- 生产者消费者或管道模型
- 混合动力车型
数据并行
在数据并行模型中,任务被分配给进程,每个任务对不同的数据执行类似类型的操作。数据并行性是对多个数据项应用单个操作的结果。
数据并行模型可以应用于共享地址空间和消息传递范例。在数据并行模型中,可以通过选择局部性保留分解、使用优化的集体交互例程或通过重叠计算和交互来减少交互开销。
数据并行模型问题的主要特征是数据并行性的强度随着问题的规模而增加,这反过来又使得使用更多的进程来解决更大的问题成为可能。
示例- 密集矩阵乘法。

任务图模型
在任务图模型中,并行性通过任务图来表达。任务图可以是平凡的,也可以是重要的。在该模型中,利用任务之间的相关性来促进局部性或最小化交互成本。该模型用于解决与任务相关的数据量相对于任务相关的计算量来说巨大的问题。分配这些任务是为了帮助提高任务之间数据移动的成本。
示例- 并行快速排序、稀疏矩阵分解以及通过分而治之方法导出的并行算法。

在这里,问题被划分为Atomics任务并以图的形式实现。每个任务都是一个独立的作业单元,依赖于一个或多个先前任务。任务完成后,先行任务的输出将传递给从属任务。具有先行任务的任务仅在其整个先行任务完成时才开始执行。当最后一个依赖任务完成时(上图中的任务 6),接收到图的最终输出。
工作池模型
在工作池模型中,任务被动态分配给进程以平衡负载。因此,任何进程都可能执行任何任务。当与任务相关的数据量相对小于与任务相关的计算量时,使用该模型。
不需要将任务预先分配到流程上。任务分配可以是集中式的,也可以是分散式的。指向任务的指针保存在物理共享列表、优先级队列、哈希表或树中,或者它们可以保存在物理分布式数据结构中。
该任务可能在一开始就可用,或者可以动态生成。如果任务是动态生成的,并且任务的分散分配,那么就需要一个终止检测算法,以便所有进程能够真正检测到整个程序的完成,并停止寻找更多的任务。
示例- 并行树搜索

主从模型
在主从模型中,一个或多个主进程生成任务并将其分配给从进程。如果出现以下情况,可以提前分配任务:
- 主人可以估计任务量,或者
- 随机分配可以令人满意地平衡负载,或者
- 奴隶在不同的时间被分配较小的任务。
该模型通常同样适用于共享地址空间或消息传递范例,因为交互自然是两种方式。
在某些情况下,一个任务可能需要分阶段完成,并且每个阶段的任务必须完成后才能生成下一阶段的任务。主从模型可以推广为分层或多级主从模型,其中顶级主站将大部分任务提供给第二级主站,第二级主站进一步将任务细分给自己的从站,并可以执行任务本身的一部分。
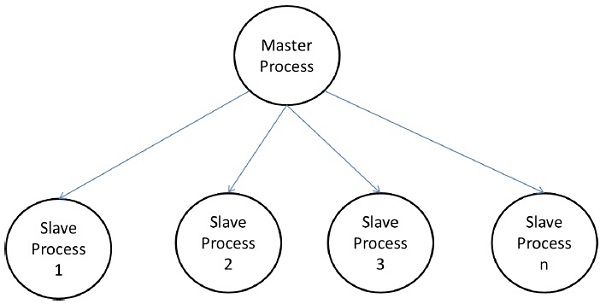
使用主从模式的注意事项
应注意确保主站不会成为拥塞点。如果任务太小或工作人员速度相对较快,则可能会发生这种情况。
选择任务时应确保执行任务的成本主导通信成本和同步成本。
异步交互可以帮助重叠交互和与主机的工作生成相关联的计算。
管道模型
它也被称为生产者-消费者模型。这里,一组数据通过一系列进程传递,每个进程都对其执行一些任务。这里,新数据的到来会导致队列中的进程执行新任务。这些进程可以形成线性或多维数组、树或带或不带循环的一般图形状的队列。
这个模型是一个生产者和消费者的链条。队列中的每个进程可以被视为队列中其前面的进程的一系列数据项的消费者,以及队列中其后面的进程的数据的生产者。队列不需要是线性链;它可以是有向图。适用于该模型的最常见交互最小化技术是与计算重叠交互。
示例- 并行 LU 分解算法。

混合动力车型
当可能需要多个模型来解决问题时,需要混合算法模型。
混合模型可以由分层应用的多个模型或顺序应用于并行算法的不同阶段的多个模型组成。
示例- 并行快速排序
并行随机存取机
并行随机存取机(PRAM)是大多数并行算法都考虑的模型。在这里,多个处理器连接到单个内存块。PRAM 模型包含 -
一组类似类型的处理器。
所有处理器共享一个公共内存单元。处理器之间只能通过共享内存进行通信。
内存访问单元 (MAU) 将处理器与单个共享内存连接起来。

这里,n个处理器可以在特定的时间单位内对n个数据执行独立的操作。这可能会导致不同处理器同时访问同一内存位置。
为了解决这个问题,对 PRAM 模型施加了以下约束 -
独占读独占写(EREW) - 这里不允许两个处理器同时读取或写入同一内存位置。
独占读取并发写入 (ERCW) - 这里不允许两个处理器同时从同一内存位置读取,但允许同时写入同一内存位置。
并发读独占写 (CREW) - 这里允许所有处理器同时从同一内存位置读取,但不允许同时写入同一内存位置。
并发读取并发写入 (CRCW) - 允许所有处理器同时读取或写入同一内存位置。
实现 PRAM 模型的方法有很多,但最突出的是 -
- 共享内存模型
- 消息传递模型
- 数据并行模型
共享内存模型
共享内存强调控制并行性而不是数据并行性。在共享内存模型中,多个进程独立地在不同的处理器上执行,但它们共享公共的内存空间。由于任何处理器活动,如果任何内存位置发生任何变化,其余处理器都可以看到。
当多个处理器访问同一内存位置时,可能会发生在任何特定时间点,多个处理器正在访问同一内存位置的情况。假设一个人正在读取该位置,另一个人正在该位置上写入。它可能会造成混乱。为了避免这种情况,实现了一些控制机制,如锁/信号量,以确保互斥。

共享内存编程已实现如下 -
线程库- 线程库允许多个控制线程在同一内存位置同时运行。线程库提供了一个通过子程序库支持多线程的接口。它包含子例程
- 创建和销毁线程
- 调度线程的执行
- 在线程之间传递数据和消息
- 保存和恢复线程上下文
线程库的示例包括 - 用于 Solaris 的 SolarisTM 线程、Linux 中实现的 POSIX 线程、Windows NT 和 Windows 2000 中可用的 Win32 线程以及作为标准 JavaTM 开发工具包 (JDK) 一部分的 JavaTM 线程。
分布式共享内存(DSM)系统- DSM 系统在松散耦合架构上创建共享内存的抽象,以便在没有硬件支持的情况下实现共享内存编程。它们实现标准库并使用现代操作系统中存在的高级用户级内存管理功能。示例包括 Tread Marks System、Munin、IVY、Shasta、Brazos 和 Cashmere。
程序注释包- 这是在具有统一内存访问特性的架构上实现的。程序注释包最著名的例子是 OpenMP。OpenMP 实现功能并行。它主要关注循环的并行化。
共享内存的概念提供了对共享内存系统的低级控制,但它往往是乏味且错误的。它比应用程序编程更适用于系统编程。
共享内存编程的优点
全局地址空间为内存提供了一种用户友好的编程方法。
由于内存距离CPU较近,进程之间的数据共享快速且统一。
无需明确指定进程之间的数据通信。
进程通信开销可以忽略不计。
这很容易学。
共享内存编程的缺点
- 它不便于携带。
- 管理数据局部性非常困难。
消息传递模型
消息传递是分布式内存系统中最常用的并行编程方法。在这里,程序员必须确定并行度。在该模型中,所有处理器都有自己的本地存储单元,并通过通信网络交换数据。

处理器使用消息传递库在它们之间进行通信。除了发送的数据外,消息还包含以下组件 -
发送消息的处理器的地址;
发送处理器中数据存储位置的起始地址;
发送数据的数据类型;
发送数据的数据大小;
消息发送到的处理器的地址;
接收处理器中数据的存储位置的起始地址。
处理器可以通过以下任何一种方法相互通信 -
- 点对点通讯
- 集体交流
- 消息传递接口
点对点通讯
点对点通信是最简单的消息传递形式。这里,消息可以通过以下任何传输模式从发送处理器发送到接收处理器 -
同步模式- 仅在收到前一条消息已发送的确认后才发送下一条消息,以保持消息的顺序。
异步模式- 要发送下一条消息,不需要收到上一条消息传送的确认。
集体交流
集体通信涉及两个以上的处理器来传递消息。以下模式允许集体通信 -
屏障- 如果通信中包含的所有处理器都运行特定的块(称为屏障块)来传递消息,则屏障模式是可能的。
广播- 广播有两种类型 -
一对多- 此处,一个具有单个操作的处理器向所有其他处理器发送相同的消息。
All-to-all - 在这里,所有处理器向所有其他处理器发送消息。
广播的消息可以分为三种类型 -
个性化- 独特的消息被发送到所有其他目标处理器。
非个性化- 所有目标处理器都会收到相同的消息。
缩减- 在缩减广播中,组中的一个处理器收集来自组中所有其他处理器的所有消息,并将它们组合成单个消息,组中的所有其他处理器都可以访问。
消息传递的优点
- 提供并行性的低级控制;
- 它是便携式的;
- 不易出错;
- 并行同步和数据分发的开销更少。
消息传递的缺点
与并行共享内存代码相比,消息传递代码通常需要更多的软件开销。
消息传递库
有许多消息传递库。在这里,我们将讨论两个最常用的消息传递库 -
- 消息传递接口 (MPI)
- 并行虚拟机 (PVM)
消息传递接口 (MPI)
它是在分布式内存系统中所有并发进程之间提供通信的通用标准。大多数常用的并行计算平台都提供至少一种消息传递接口的实现。它被实现为称为库的预定义函数的集合,可以从 C、C++、Fortran 等语言中调用。与其他消息传递库相比,MPI 既快速又可移植。
消息传递接口的优点
仅运行在共享内存架构或分布式内存架构上;
每个处理器都有自己的局部变量;
与大型共享内存计算机相比,分布式内存计算机更便宜。
消息传递接口的缺点
- 并行算法需要更多的编程更改;
- 有时很难调试;和
- 在节点之间的通信网络中表现不佳。
并行虚拟机 (PVM)
PVM 是一种便携式消息传递系统,旨在连接单独的异构主机以形成单个虚拟机。它是单个可管理的并行计算资源。通过使用内存和许多计算机的聚合能力,可以更经济有效地解决超导研究、分子动力学模拟和矩阵算法等大型计算问题。它管理不兼容计算机体系结构网络中的所有消息路由、数据转换、任务调度。
PVM的特点
- 非常容易安装和配置;
- 多个用户可以同时使用PVM;
- 一个用户可以执行多个应用程序;
- 这是一个小包装;
- 支持C、C++、Fortran;
- 对于给定的 PVM 程序运行,用户可以选择机器组;
- 这是一个消息传递模型,
- 基于流程的计算;
- 支持异构架构。
数据并行编程
数据并行编程模型的主要焦点是同时对数据集执行操作。数据集被组织成某种结构,如数组、超立方体等。处理器集体对同一数据结构执行操作。每个任务都在同一数据结构的不同分区上执行。
它具有限制性,因为并非所有算法都可以根据数据并行性来指定。这就是数据并行性不通用的原因。
数据并行语言有助于指定数据分解和到处理器的映射。它还包括数据分布语句,允许程序员控制数据(例如,哪些数据将传输到哪个处理器),以减少处理器内的通信量。
并行算法-结构
要正确应用任何算法,选择正确的数据结构非常重要。这是因为与对另一个数据结构执行相同的操作相比,对一个数据结构执行的特定操作可能需要更多的时间。
示例- 要使用数组访问集合中的第 i 个元素,可能需要恒定的时间,但通过使用链表,执行相同操作所需的时间可能会变成多项式。
因此,数据结构的选择必须考虑架构和要执行的操作类型。
以下数据结构常用于并行编程 -
- 链表
- 数组
- 超立方网络
链表
链表是具有通过指针连接的零个或多个节点的数据结构。节点可能占用也可能不占用连续的内存位置。每个节点有两个或三个部分 - 一个数据部分存储数据,另外两个是存储前一个或下一个节点的地址的链接字段。第一个节点的地址存储在称为head 的外部指针中。最后一个节点称为尾部,通常不包含任何地址。
链表分为三种类型 -
- 单链表
- 双向链表
- 循环链表
单链表
单链表的一个节点包含数据和下一个节点的地址。称为head 的外部指针存储第一个节点的地址。

双向链表
双向链表的节点包含数据以及前一个和下一个节点的地址。称为head 的外部指针存储第一个节点的地址,称为tail的外部指针存储最后一个节点的地址。

循环链表
循环链表与单链表非常相似,只是最后一个节点保存了第一个节点的地址。

数组
数组是一种数据结构,我们可以在其中存储相似类型的数据。它可以是一维或多维的。数组可以静态或动态创建。
在静态声明的数组中,数组的维数和大小在编译时已知。
在动态声明的数组中,数组的维数和大小在运行时是已知的。
对于共享内存编程,数组可以用作公共内存,而对于数据并行编程,可以通过划分为子数组来使用数组。
超立方网络
超立方体架构对于每个任务必须与其他任务通信的并行算法很有帮助。超立方体拓扑可以轻松嵌入其他拓扑,例如环形和网状拓扑。它也称为 n 立方体,其中n是维度数。超立方体可以递归地构造。


并行算法 - 设计技术
为并行算法选择合适的设计技术是最困难和最重要的任务。大多数并行编程问题可能有不止一种解决方案。在本章中,我们将讨论以下并行算法的设计技术 -
- 分而治之
- 贪心法
- 动态规划
- 回溯
- 分支与定界
- 线性规划
分而治之法
在分而治之的方法中,问题被分为几个小子问题。然后对子问题进行递归求解并组合得到原问题的解。
分而治之的方法涉及每个级别的以下步骤 -
Divide - 将原始问题分为子问题。
征服- 子问题递归解决。
组合- 将子问题的解决方案组合在一起以获得原始问题的解决方案。
分而治之的方法应用于以下算法 -
- 二分查找
- 快速排序
- 归并排序
- 整数乘法
- 矩阵求逆
- 矩阵乘法
贪心法
在优化解的贪心算法中,任何时刻都会选择最好的解。贪心算法很容易应用于复杂问题。它决定哪一步将在下一步中提供最准确的解决方案。
该算法被称为贪婪算法,因为当提供较小实例的最优解决方案时,该算法不会将整个程序视为一个整体。一旦考虑了一个解决方案,贪心算法就不会再考虑相同的解决方案。
贪婪算法从尽可能小的组成部分递归地创建一组对象。递归是解决问题的过程,其中特定问题的解决方案取决于该问题的较小实例的解决方案。
动态规划
动态规划是一种优化技术,它将问题划分为更小的子问题,在解决每个子问题后,动态规划将所有解决方案组合起来以获得最终解决方案。与分而治之的方法不同,动态规划多次重复使用子问题的解决方案。
斐波那契数列的递归算法是动态规划的一个例子。
回溯算法
回溯是一种解决组合问题的优化技术。它适用于程序和现实生活中的问题。八皇后问题、数独谜题和走迷宫是使用回溯算法的常见例子。
在回溯中,我们从满足所有所需条件的可能解决方案开始。然后我们进入下一个级别,如果该级别没有产生令人满意的解决方案,我们将返回一个级别并从一个新选项开始。
分支定界
分支定界算法是一种获得问题最优解决方案的优化技术。它在解决方案的整个空间中寻找给定问题的最佳解决方案。待优化函数的边界与最新最佳解决方案的值合并。它允许算法完全找到解空间的部分。
分支定界搜索的目的是维持到达目标的最低成本路径。一旦找到解决方案,就可以不断改进该解决方案。分支定界搜索在深度有界搜索和深度优先搜索中实现。
线性规划
线性规划描述了一类广泛的优化作业,其中优化标准和约束都是线性函数。它是一种获得最佳结果(例如最大利润、最短路径或最低成本)的技术。
在此编程中,我们有一组变量,必须为它们分配绝对值以满足一组线性方程并最大化或最小化给定的线性目标函数。
并行算法-矩阵乘法
矩阵是按固定行数和列数排列的一组数值和非数值数据。矩阵乘法是并行计算中重要的乘法设计。在这里,我们将讨论矩阵乘法在网格和超立方体等各种通信网络上的实现。网状网络和超立方体具有更高的网络连接性,因此它们比其他网络(如环形网络)允许更快的算法。
网状网络
一组节点形成 p 维网格的拓扑称为网状拓扑。这里,所有边都平行于网格轴,并且所有相邻节点可以相互通信。
总节点数=(行节点数)×(列节点数)
可以使用以下因素评估网状网络 -
- 直径
- 二分宽度
直径- 在网状网络中,两个节点之间的最长距离是其直径。具有kP个节点的 p 维网状网络的直径为p(k–1)。
二分宽度- 二分宽度是将网状网络分成两半所需的最小边数。
使用网状网络的矩阵乘法
我们考虑了具有环绕连接的 2D 网状网络 SIMD 模型。我们将设计一种算法,在特定时间内使用 n 2 个处理器将两个 n × n 数组相乘。
矩阵 A 和 B 分别具有元素 a ij和 b ij。处理元件PE ij表示a ij和b ij。排列矩阵 A 和 B,使每个处理器都有一对要相乘的元素。矩阵A的元素将向左移动,矩阵B的元素将向上移动。矩阵 A 和 B 中元素位置的这些变化为每个处理元素 PE 提供了一对要相乘的新值。
算法步骤
- 交错两个矩阵。
- 计算所有乘积,a ik × b kj
- 步骤 2 完成后计算总和。
算法
Procedure MatrixMulti
Begin
for k = 1 to n-1
for all Pij; where i and j ranges from 1 to n
ifi is greater than k then
rotate a in left direction
end if
if j is greater than k then
rotate b in the upward direction
end if
for all Pij ; where i and j lies between 1 and n
compute the product of a and b and store it in c
for k= 1 to n-1 step 1
for all Pi;j where i and j ranges from 1 to n
rotate a in left direction
rotate b in the upward direction
c=c+aXb
End
超立方网络
超立方体是一种 n 维构造,其中边相互垂直且长度相同。n 维超立方体也称为 n 立方体或 n 维立方体。
2k节点超立方体的特点
- 直径 = k
- 二分宽度 = 2 k–1
- 边数 = k
使用超立方网络的矩阵乘法
超立方网络的一般规范 -
令N = 2 m为处理器总数。令处理器为 P 0, P 1 …..P N-1。
设 i 和 i b为两个整数,0 < i,i b < N-1,其二进制表示形式仅在位置 b 上不同,0 < b < k–1。
让我们考虑两个 n × n 矩阵,矩阵 A 和矩阵 B。
步骤 1 - 矩阵 A 和矩阵 B 的元素被分配给 n 3 个处理器,使得位置 i、j、k 的处理器将具有ji和 b ik。
步骤 2 - 位置 (i,j,k) 的所有处理器计算乘积
C(i,j,k) = A(i,j,k) × B(i,j,k)
步骤 3 - 总和 C(0,j,k) = ΣC(i,j,k),0 ≤ i ≤ n-1,其中 0 ≤ j,k < n–1。
块矩阵
块矩阵或分区矩阵是一个矩阵,其中每个元素本身代表一个单独的矩阵。这些单独的部分称为块或子矩阵。
例子


在图(a)中,X是分块矩阵,其中A、B、C、D本身就是矩阵。图(f)显示了总矩阵。
块矩阵乘法
当两个分块矩阵是方阵时,它们的乘法就像我们执行简单矩阵乘法一样。例如,

并行算法-排序
排序是按特定顺序排列组中元素的过程,即升序、降序、字母顺序等。这里我们将讨论以下内容 -
- 枚举排序
- 奇偶转置排序
- 并行归并排序
- 超快速排序
对元素列表进行排序是一种非常常见的操作。当我们必须对大量数据进行排序时,顺序排序算法可能不够高效。因此,排序时采用并行算法。
枚举排序
枚举排序是一种通过查找已排序列表中每个元素的最终位置来排列列表中所有元素的方法。它是通过将每个元素与所有其他元素进行比较并找到具有较小值的元素的数量来完成的。
因此,对于任意两个元素 a i和 a j ,以下任何一种情况都必须为真 -
- a i < a j
- a i > a j
- a i = a j
算法
procedure ENUM_SORTING (n)
begin
for each process P1,j do
C[j] := 0;
for each process Pi, j do
if (A[i] < A[j]) or A[i] = A[j] and i < j) then
C[j] := 1;
else
C[j] := 0;
for each process P1, j do
A[C[j]] := A[j];
end ENUM_SORTING
奇偶转置排序
奇偶转置排序基于冒泡排序技术。它比较两个相邻的数字,如果第一个数字大于第二个数字,则将它们交换,以获得升序列表。相反的情况适用于降序序列。奇偶转置排序分两个阶段进行:奇数阶段和偶数阶段。在这两个阶段中,进程都会与其右侧的相邻数字交换数字。

算法
procedure ODD-EVEN_PAR (n)
begin
id := process's label
for i := 1 to n do
begin
if i is odd and id is odd then
compare-exchange_min(id + 1);
else
compare-exchange_max(id - 1);
if i is even and id is even then
compare-exchange_min(id + 1);
else
compare-exchange_max(id - 1);
end for
end ODD-EVEN_PAR
并行归并排序
归并排序首先将未排序的列表划分为尽可能小的子列表,将其与相邻列表进行比较,然后按已排序的顺序将其合并。它通过遵循分治算法很好地实现了并行性。

算法
procedureparallelmergesort(id, n, data, newdata)
begin
data = sequentialmergesort(data)
for dim = 1 to n
data = parallelmerge(id, dim, data)
endfor
newdata = data
end
超快速排序
超快速排序是快速排序在超立方体上的实现。其步骤如下 -
- 在每个节点之间划分未排序的列表。
- 在本地对每个节点进行排序。
- 从节点 0 开始,广播中值。
- 在本地拆分每个列表,然后在最高维度上交换两半。
- 并行重复步骤 3 和 4,直到维度达到 0。
算法
procedure HYPERQUICKSORT (B, n)
begin
id := process’s label;
for i := 1 to d do
begin
x := pivot;
partition B into B1 and B2 such that B1 ≤ x < B2;
if ith bit is 0 then
begin
send B2 to the process along the ith communication link;
C := subsequence received along the ith communication link;
B := B1 U C;
endif
else
send B1 to the process along the ith communication link;
C := subsequence received along the ith communication link;
B := B2 U C;
end else
end for
sort B using sequential quicksort;
end HYPERQUICKSORT
并行搜索算法
搜索是计算机科学的基本操作之一。它用于我们需要查找元素是否在给定列表中的所有应用程序。在本章中,我们将讨论以下搜索算法 -
- 分而治之
- 深度优先搜索
- 广度优先搜索
- 最佳优先搜索
分而治之
在分而治之的方法中,问题被分为几个小子问题。然后对子问题进行递归求解并组合得到原问题的解。
分而治之的方法涉及每个级别的以下步骤 -
Divide - 将原始问题分为子问题。
征服- 子问题递归解决。
组合- 将子问题的解决方案组合起来以获得原始问题的解决方案。
二分查找是分而治之算法的一个例子。
伪代码
Binarysearch(a, b, low, high)
if low < high then
return NOT FOUND
else
mid ← (low+high) / 2
if b = key(mid) then
return key(mid)
else if b < key(mid) then
return BinarySearch(a, b, low, mid−1)
else
return BinarySearch(a, b, mid+1, high)
深度优先搜索
深度优先搜索(或 DFS)是一种用于搜索树或无向图数据结构的算法。这里的概念是从称为根的起始节点开始,并在同一分支中尽可能远地遍历。如果我们得到一个没有后继节点的节点,我们返回并继续尚未访问的顶点。
深度优先搜索的步骤
考虑一个先前未访问过的节点(根)并将其标记为已访问。
访问第一个相邻的后继节点并将其标记为已访问。
如果所考虑的节点的所有后继节点都已被访问或者没有更多的后继节点,则返回其父节点。
伪代码
令v为图G中搜索开始的顶点。
DFS(G,v)
Stack S := {};
for each vertex u, set visited[u] := false;
push S, v;
while (S is not empty) do
u := pop S;
if (not visited[u]) then
visited[u] := true;
for each unvisited neighbour w of u
push S, w;
end if
end while
END DFS()
广度优先搜索
广度优先搜索(或 BFS)是一种用于搜索树或无向图数据结构的算法。这里,我们从一个节点开始,然后访问同一层中的所有相邻节点,然后移动到下一层中的相邻后继节点。这也称为逐级搜索。
广度优先搜索的步骤
- 从根节点开始,将其标记为已访问。
- 由于根节点在同级中没有节点,因此进入下一级。
- 访问所有相邻节点并将其标记为已访问。
- 进入下一层,访问所有未访问过的相邻节点。
- 继续这个过程,直到访问完所有节点。
伪代码
令v为图G中搜索开始的顶点。
BFS(G,v)
Queue Q := {};
for each vertex u, set visited[u] := false;
insert Q, v;
while (Q is not empty) do
u := delete Q;
if (not visited[u]) then
visited[u] := true;
for each unvisited neighbor w of u
insert Q, w;
end if
end while
END BFS()
最佳优先搜索
最佳优先搜索是一种遍历图以以最短可能路径到达目标的算法。与 BFS 和 DFS 不同,最佳优先搜索遵循评估函数来确定接下来最适合遍历哪个节点。
最佳优先搜索的步骤
- 从根节点开始,将其标记为已访问。
- 找到下一个适当的节点并将其标记为已访问。
- 进入下一级并找到适当的节点并将其标记为已访问。
- 继续此过程直至达到目标。
伪代码
BFS( m )
Insert( m.StartNode )
Until PriorityQueue is empty
c ← PriorityQueue.DeleteMin
If c is the goal
Exit
Else
Foreach neighbor n of c
If n "Unvisited"
Mark n "Visited"
Insert( n )
Mark c "Examined"
End procedure
图算法
图是一种抽象符号,用于表示对象对之间的连接。图表包括 -
顶点- 图中互连的对象称为顶点。顶点也称为节点。
边- 边是连接顶点的链接。
有两种类型的图表 -
有向图- 在有向图中,边有方向,即边从一个顶点到另一个顶点。
无向图- 在无向图中,边没有方向。
图形着色
图着色是一种为图的顶点分配颜色的方法,这样相邻的两个顶点就不会具有相同的颜色。一些图形着色问题是 -
顶点着色- 一种对图的顶点进行着色的方法,以便没有两个相邻顶点共享相同的颜色。
边缘着色- 这是为每个边缘分配颜色的方法,以便没有两个相邻边缘具有相同的颜色。
面着色- 它将颜色分配给平面图的每个面或区域,以便共享公共边界的两个面不会具有相同的颜色。
色数
色数是为图形着色所需的最小颜色数。例如,下图的色数为3。

图形着色的概念应用于准备时间表、移动射频分配、数独、寄存器分配和地图着色。
图形着色的步骤
将n维数组中每个处理器的初始值设置为1。
现在,要将特定颜色分配给顶点,请确定该颜色是否已分配给相邻顶点。
如果处理器在相邻顶点中检测到相同的颜色,则会将其在数组中的值设置为 0。
进行n 2次比较后,如果数组中有任何元素为1,则它是有效的着色。
图形着色的伪代码
begin
create the processors P(i0,i1,...in-1) where 0_iv < m, 0 _ v < n
status[i0,..in-1] = 1
for j varies from 0 to n-1 do
begin
for k varies from 0 to n-1 do
begin
if aj,k=1 and ij=ikthen
status[i0,..in-1] =0
end
end
ok = ΣStatus
if ok > 0, then display valid coloring exists
else
display invalid coloring
end
最小生成树
其所有边的权重(或长度)总和小于图 G 的所有其他可能的生成树的生成树称为最小生成树或最小成本生成树。下图显示了一个加权连通图。

上图的一些可能的生成树如下所示 -




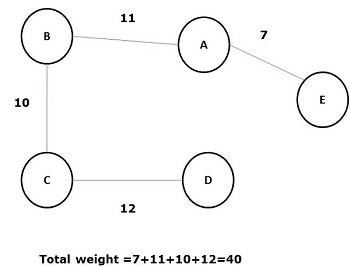


在上述所有生成树中,图(d)是最小生成树。最小成本生成树的概念应用于旅行商问题、设计电子电路、设计高效网络和设计高效路由算法。
为了实现最小成本生成树,使用以下两种方法 -
- 普里姆算法
- 克鲁斯卡尔算法
普里姆算法
Prim的算法是一种贪心算法,它帮助我们找到带权无向图的最小生成树。它首先选择一个顶点,并找到该顶点上具有最低权重的边。
Prim算法的步骤
选择任意顶点,例如图 G 的v 1 。
选择一条边,例如 G 的 e 1,使得 e 1 = v 1 v 2且 v 1 ≠ v 2并且 e 1在图 G 中与 v 1相关的边中具有最小权重。
现在,按照步骤 2,选择入射到 v 2上的最小加权边。
继续此操作,直到选择了 n–1 条边。这里n是顶点的数量。

最小生成树是 -

克鲁斯卡尔算法
Kruskal 算法是一种贪心算法,它可以帮助我们找到连通加权图的最小生成树,并在每一步添加递增的成本弧。它是一种最小生成树算法,可找到连接森林中任意两棵树的最小可能权重边。
克鲁斯卡尔算法的步骤
选择权重最小的边;假设图 G 的e 1且 e 1不是循环。
选择连接到 e 1的下一个最小加权边。
继续此操作,直到选择了 n–1 条边。这里n是顶点的数量。

上图的最小生成树是 -

最短路径算法
最短路径算法是一种寻找从源节点(S)到目的节点(D)的最小成本路径的方法。在这里,我们将讨论摩尔算法,也称为广度优先搜索算法。
摩尔算法
标记源顶点 S 并将其标记为i并设置i=0。
查找与标记为i 的顶点相邻的所有未标记顶点。如果没有顶点连接到顶点 S,则顶点 D 不会连接到 S。如果有顶点连接到 S,则将它们标记为i+1。
如果D被标记,则转到步骤4,否则转到步骤2以增加i=i+1。
找到最短路径的长度后停止。