在数轴上绘制有理数

有理数是分数，并在数轴上绘制如下。

表示有理数的基本规则 在数轴上

  • 如果有理数（分数）是真数，则它位于 0 和 1 之间。

  • 如果有理数（分数）不正确，则首先将其转换为带分数，然后再将给定的有理数转换为带分数。位于整数和下一个整数之间。

我们使用以下步骤来表示有理数或分数，例如数轴上的$\frac{5}{7}$ 。

步骤 1 - 我们画一条数轴。

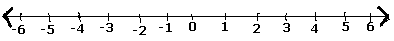
10.1 在数轴上绘制有理数

步骤 2 - 由于数字$\frac{5}{7}$是正数，因此它位于零的右侧。

步骤 3 - 因此，在零标记之后，我们有$\frac{1}{7}, \: \frac{2}{7}, \: \frac{3}{7}, \: \frac{4} {7}、\:\frac{5}{7}、\:\frac{6}{7}、$和 ( $\frac{7}{7}$ = 1)。

步骤 4 -数轴上的有理数$\frac{5}{7}$如下所示。

10.2 在数轴上绘制有理数

在下面的数轴上绘制$\frac{1}{4}$和$1\frac{2}{4}$

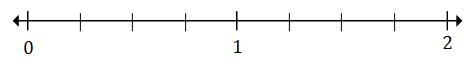
在数轴上绘制有理数 10.3

解决方案

步骤1：

$\frac{1}{4}$ (A) 位于 0 和 1 之间；$1\frac{2}{4}$ (B) 位于 1 和 2 之间

第2步：

每个除法分为四部分，因为分数的底部是 4。

$\frac{1}{4}$是0之后的第一个标记，因此A点代表$\frac{1}{4}$

$1\frac{2}{4}$是1之后的第二个标记，所以B点代表$1\frac{2}{4}$

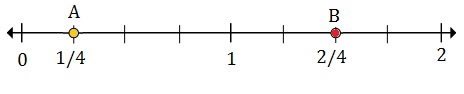
在数轴上绘制有理数 10.4

在下面的数轴上绘制$\frac{5}{8}$和$2\frac{3}{8}$

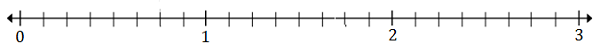
在数轴上绘制有理数 10.5

解决方案

步骤1：

$\frac{5}{8}$ 8 (A) 位于 0 和 1 之间；$2\frac{3}{8}$ (B) 位于 2 和 3 之间

第2步：

每个除法分为八个部分，因为分数的底部是 8。

$\frac{5}{8}$是0之后的第五个标记，因此A点代表$\frac{5}{8}$

$2\frac{3}{8}$是2之后的第三个标记，所以B点代表$2\frac{3}{8}$

在数轴上绘制有理数 10.6