PyTorch - 循环神经网络

循环神经网络是一种面向深度学习的算法，遵循顺序方法。在神经网络中，我们总是假设每个输入和输出都独立于所有其他层。这些类型的神经网络被称为循环神经网络，因为它们以顺序方式执行数学计算，完成一项又一项任务。

下图详细说明了循环神经网络的完整方法和工作原理 -

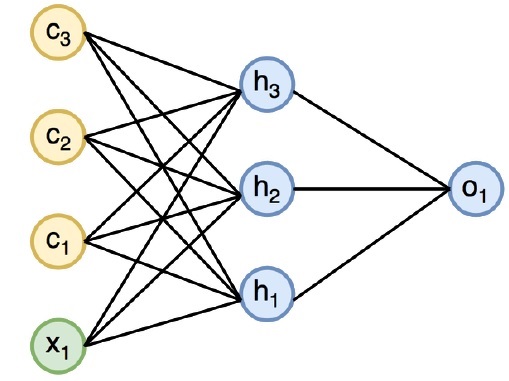
循环神经网络Ex

在上图中，c1、c2、c3 和 x1 被视为输入，其中包括一些隐藏输入值，即 h1、h2 和 h3，分别传递 o1 的输出。我们现在将重点关注如何实现 PyTorch 在循环神经网络的帮助下创建正弦波。

在训练期间，我们将遵循一种每次使用一个数据点对模型进行训练的方法。输入序列x由20个数据点组成，目标序列被认为与输入序列相同。

步骤1

使用以下代码导入实现循环神经网络所需的包 -

import torch
from torch.autograd import Variable
import numpy as np
import pylab as pl
import torch.nn.init as init

第2步

我们将设置模型超参数，输入层的大小设置为 7。将有 6 个上下文神经元和 1 个输入神经元用于创建目标序列。

dtype = torch.FloatTensor
input_size, hidden_size, output_size = 7, 6, 1
epochs = 300
seq_length = 20
lr = 0.1
data_time_steps = np.linspace(2, 10, seq_length + 1)
data = np.sin(data_time_steps)
data.resize((seq_length + 1, 1))

x = Variable(torch.Tensor(data[:-1]).type(dtype), requires_grad=False)
y = Variable(torch.Tensor(data[1:]).type(dtype), requires_grad=False)

我们将生成训练数据，其中 x 是输入数据序列，y 是所需的目标序列。

步骤3

使用零均值正态分布在循环神经网络中初始化权重。W1 将代表接受输入变量，w2 将代表生成的输出，如下所示 -

w1 = torch.FloatTensor(input_size, 
hidden_size).type(dtype)
init.normal(w1, 0.0, 0.4)
w1 = Variable(w1, requires_grad = True)
w2 = torch.FloatTensor(hidden_size, output_size).type(dtype)
init.normal(w2, 0.0, 0.3)
w2 = Variable(w2, requires_grad = True)

步骤4

现在，创建一个唯一定义神经网络的前馈函数非常重要。

def forward(input, context_state, w1, w2):
   xh = torch.cat((input, context_state), 1)
   context_state = torch.tanh(xh.mm(w1))
   out = context_state.mm(w2)
   return (out, context_state)

步骤5

下一步是开始循环神经网络正弦波实现的训练过程。外循环迭代每个循环，内循环迭代序列的元素。在这里，我们还将计算均方误差 (MSE)，这有助于预测连续变量。

for i in range(epochs):
   total_loss = 0
   context_state = Variable(torch.zeros((1, hidden_size)).type(dtype), requires_grad = True)
   for j in range(x.size(0)):
      input = x[j:(j+1)]
      target = y[j:(j+1)]
      (pred, context_state) = forward(input, context_state, w1, w2)
      loss = (pred - target).pow(2).sum()/2
      total_loss += loss
      loss.backward()
      w1.data -= lr * w1.grad.data
      w2.data -= lr * w2.grad.data
      w1.grad.data.zero_()
      w2.grad.data.zero_()
      context_state = Variable(context_state.data)
   if i % 10 == 0:
      print("Epoch: {} loss {}".format(i, total_loss.data[0]))

context_state = Variable(torch.zeros((1, hidden_size)).type(dtype), requires_grad = False)
predictions = []

for i in range(x.size(0)):
   input = x[i:i+1]
   (pred, context_state) = forward(input, context_state, w1, w2)
   context_state = context_state
   predictions.append(pred.data.numpy().ravel()[0])

步骤6

现在，是时候按照需要的方式绘制正弦波了。

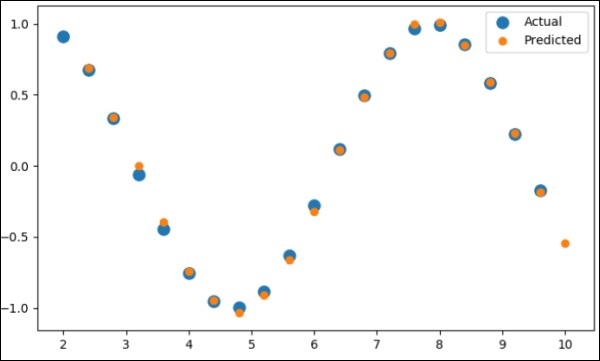
pl.scatter(data_time_steps[:-1], x.data.numpy(), s = 90, label = "Actual")
pl.scatter(data_time_steps[1:], predictions, label = "Predicted")
pl.legend()
pl.show()

输出

上述过程的输出如下 -

正弦波