自适应共振理论

该网络由 Stephen Grossberg 和 Gail Carpenter 于 1987 年开发。它基于竞争，采用无监督学习模型。自适应共振理论（ART）网络，顾名思义，总是对新的学习（自适应）开放，而不会失去旧的模式（共振）。基本上，ART 网络是一个向量分类器，它接受输入向量并根据它最类似于哪个存储模式将其分类为一个类别。

营运负责人

ART分类的主要操作可以分为以下阶段 -

识别阶段- 将输入向量与输出层中每个节点处呈现的分类进行比较。如果神经元的输出与所应用的分类最匹配，则其输出变为“1”，否则变为“0”。
比较阶段- 在此阶段，完成输入向量与比较层向量的比较。重置的条件是相似度小于警戒参数。
搜索阶段- 在此阶段，网络将搜索重置以及上述阶段中完成的匹配。因此，如果没有重置并且匹配相当好，那么分类就结束了。否则，将重复该过程，并且必须发送其他存储的模式以找到正确的匹配。

艺术1

它是 ART 的一种，旨在对二进制向量进行聚类。我们可以通过它的架构来理解这一点。

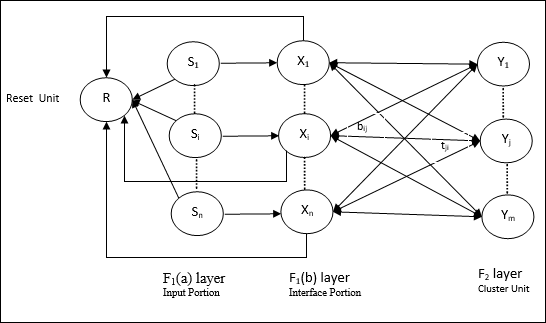
ART1的架构

它由以下两个单元组成 -

计算单元- 由以下部分组成 -

输入单元（F ₁层） - 它还具有以下两个部分 -
- F ₁ (a) 层（输入部分） - 在 ART1 中，该部分不会进行任何处理，而只有输入向量。_{它与F 1} (b)层(界面部分)连接。
- F ₁ (b) 层（接口部分） - 该部分将输入部分的信号与 F ₂层的信号相结合。F ₁ (b)层通过自下而上权重b _ij连接到F ₂层，并且F ₂层通过自上而下权重t _ji连接到F ₁ (b)层。
簇单元（F ₂层） - 这是一个竞争层。选择具有最大净输入的单元来学习输入模式。所有其他集群单元的激活均设置为 0。
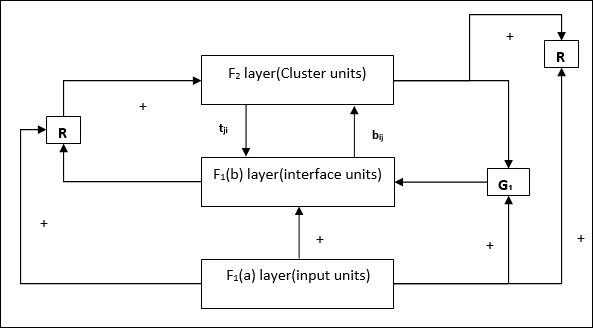
重置机制- 该机制的工作基于自上而下权重和输入向量之间的相似性。现在，如果这种相似度小于警惕参数，则不允许集群学习该模式，并且会发生休息。

补充单元- 实际上，重置机制的问题在于， F ₂层必须在某些条件下受到抑制，并且在发生某些学习时也必须可用。这就是为什么添加两个补充单元（即G ₁和G _{2 ）}以及复位单元R的原因。它们被称为增益控制单元。这些单元接收信号并向网络中存在的其他单元发送信号。“+”表示兴奋信号，“-”表示抑制信号。

使用的参数

使用以下参数 -

n - 输入向量中的分量数量
m - 可以形成的最大簇数
b _ij − F ₁ (b) 到 F ₂层的权重，即自下而上的权重
t _ji − F ₂到 F ₁ (b) 层的权重，即自上而下的权重
ρ - 警戒参数
||x|| − 向量 x 的范数

算法

步骤 1 - 初始化学习率、警戒参数和权重，如下 -

$$\alpha\:>\:1\:\:和\:\:0\:<\rho\:\leq\:1$$

$$0\:<\:b_{ij}(0)\:<\:\frac{\alpha}{\alpha\:-\:1\:+\:n}\:\:和\:\: t_{ij}(0)\:=\:1$$

步骤 2 - 当停止条件不成立时，继续步骤 3-9。

步骤 3 - 对于每个训练输入继续步骤 4-6。

步骤 4 - 设置所有 F ₁ (a) 和 F ₁单元的激活，如下所示

F ₂ = 0 且 F ₁ (a) = 输入向量

步骤 5 - 从 F ₁ (a) 层到 F ₁ (b) 层的输入信号必须像这样发送

$$s_{i}\:=\:x_{i}$$

步骤 6 - 对于每个受抑制的 F ₂节点

$y_{j}\:=\:\sum_i b_{ij}x_{i}$条件是y _j ≠ -1

步骤 7 - 当重置为真时，执行步骤 8-10。

步骤 8 -为所有节点j找到y _J ≥ y _j的J

步骤 9 - 再次计算 F ₁ (b)上的激活，如下所示

$$x_{i}\:=\:sitJi$$

步骤 10 - 现在，在计算向量x和向量s的范数后，我们需要检查重置条件，如下所示 -

如果||x||/ ||s|| < 警戒参数ρ，⁡然后⁡抑制⁡节点J并转到步骤 7

否则如果||x||/ ||s|| ≥ 警戒参数ρ，则进一步进行。

步骤 11 - 节点J的权重更新可以按如下方式完成 -

$$b_{ij}(新)\:=\:\frac{\alpha x_{i}}{\alpha\:-\:1\:+\:||x||}$$

$$t_{ij}（新）\:=\:x_{i}$$

步骤 12 - 必须检查算法的停止条件，可能如下 -

体重没有任何变化。
不对单位执行重置。
已达到最大纪元数。