人工神经网络 - 快速指南

人工神经网络 - 基本概念

神经网络是并行计算设备，基本上是尝试建立大脑的计算机模型。主要目标是开发一种比传统系统更快地执行各种计算任务的系统。这些任务包括模式识别和分类、近似、优化和数据聚类。

什么是人工神经网络？

人工神经网络（ANN）是一种高效的计算系统，其中心主题借鉴了生物神经网络的类比。人工神经网络也被称为“人工神经系统”、“并行分布式处理系统”或“连接主义系统”。人工神经网络获取大量单元，这些单元以某种模式互连，以允许单元之间进行通信。这些单元也称为节点或神经元，是并行操作的简单处理器。

每个神经元通过连接链路与其他神经元连接。每个连接链路都与一个权重相关联，该权重具有有关输入信号的信息。这是神经元解决特定问题最有用的信息，因为权重通常会激发或抑制正在传递的信号。每个神经元都有一个内部状态，称为激活信号。组合输入信号和激活规则后产生的输出信号可以被发送到其他单元。

人工神经网络简史

ANN的历史可以分为以下三个时代 -

1940 年代至 1960 年代的 ANN

这个时代的一些关键发展如下：

1943 年- 人们认为神经网络的概念始于生理学家 Warren McCulloch 和数学家 Walter Pitts 的工作，当时他们在 1943 年使用电路建模了一个简单的神经网络，以描述大脑中的神经元如何工作工作。
1949 年- Donald Hebb 的书《Behave的组织》提出了这样一个事实：一个神经元被另一个神经元重复激活会在每次使用时增加其强度。
1956 - 泰勒提出了联想记忆网络。
1958 年- Rosenblatt 发明了一种名为 Perceptron 的 McCulloch 和 Pitts 神经元模型的学习方法。
1960 年– Bernard Widrow 和 Marcian Hoff 开发了名为“ADALINE”和“MADALINE”的型号。

1960 年代至 1980 年代的 ANN

这个时代的一些关键发展如下：

1961 - Rosenblatt 进行了一次不成功的尝试，但提出了多层网络的“反向传播”方案。
1964 - 泰勒构建了一个赢家通吃的电路，并在输出单元之间进行了抑制。
1969 年- 多层感知器 (MLP) 由 Minsky 和 Papert 发明。
1971 – Kohonen 开发了联想记忆。
1976 年- Stephen Grossberg 和 Gail Carpenter 开发了自适应共振理论。

ANN 从 20 世纪 80 年代至今

这个时代的一些关键发展如下：

1982 年– 主要发展是 Hopfield 的能源方法。
1985 – 玻尔兹曼机由 Ackley、Hinton 和 Sejnowski 开发。
1986 年- Rumelhart、Hinton 和 Williams 引入了广义 Delta 规则。
1988 – Kosko 开发了二进制关联存储器（BAM），并在 ANN 中提出了模糊逻辑的概念。

历史回顾表明，这一领域已经取得了重大进展。基于神经网络的芯片正在兴起，并且正在开发解决复杂问题的应用程序。当然，今天是神经网络技术的过渡时期。

生物神经元

神经细胞（神经元）是一种处理信息的特殊生物细胞。据估计，神经元数量巨大，大约有10 ^{11 个}，神经元之间的相互连接也很多，大约有10 ^{15 个}。

原理图，示意图

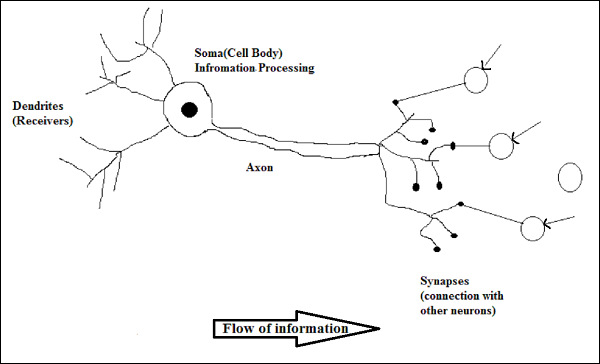
生物神经元的工作

如上图所示，一个典型的神经元由以下四个部分组成，借助这些部分我们可以解释其工作原理 -

树突- 它们是树状分支，负责从其连接的其他神经元接收信息。从另一种意义上来说，我们可以说它们就像神经元的耳朵。
Soma - 它是神经元的细胞体，负责处理从树突接收的信息。
轴突- 它就像神经元发送信息的电缆。
突触- 它是轴突和其他神经元树突之间的连接。

ANN 与 BNN

在了解人工神经网络 (ANN) 和生物神经网络 (BNN) 之间的差异之前，让我们先根据这两者之间的术语来了解一下相似之处。

生物神经网络（BNN）	人工神经网络 (ANN)
索马	节点
树突	输入
突触	重量或互连
轴突	输出

下表显示了基于提到的一些标准的 ANN 和 BNN 之间的比较。

标准	神经网络	神经网络
加工	大规模并行，缓慢但优于 ANN	大规模并行，速度快但不如 BNN
尺寸	10 ^{11 个}神经元和 10 ^{15 个}互连	10 ²至 10 ^{4 个}节点（主要取决于应用类型和网络设计者）
学习	他们可以容忍暧昧	需要非常精确、结构化和格式化的数据来容忍歧义
容错能力	即使部分损坏也会导致性能下降	它具有强大的性能，因此具有容错的潜力
存储容量	将信息存储在突触中	将信息存储在连续的内存位置

人工神经网络模型

下图展示了 ANN 的一般模型及其处理过程。

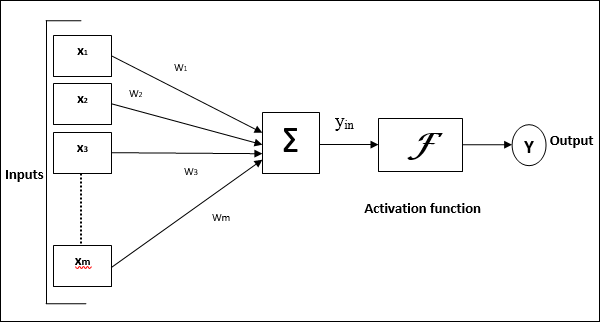
对于上述人工神经网络的通用模型，净输入可以计算如下 -

y i n = x 1 . w 1 + x 2 . w 2 + x 3 . w 3 \dots x m . w m

$y_{in}\:=\:x_{1}.w_{1}\:+\:x_{2}.w_{2}\:+\:x_{3}.w_{3}\:\dotso\: x_{m}.w_{m}$

即，净输入 $y_{in}\:=\:\sum_i^m\:x_{i}.w_{i}$

可以通过对净输入应用激活函数来计算输出。

Y = F (y i n)

$Y\:=\:F(y_{in})$

输出 = 函数（计算出的净输入）

人工神经网络 - 构建模块

ANN 的处理取决于以下三个构建块 -

网络拓扑结构
权重或学习的调整
激活函数

在本章中，我们将详细讨论 ANN 的这三个构建模块

网络拓扑结构

网络拓扑是网络及其节点和连接线的排列。根据拓扑结构，人工神经网络可以分为以下几种 -

前馈网络

它是一个非循环网络，具有分层的处理单元/节点，并且一层中的所有节点都与前一层的节点连接。连接对它们有不同的权重。没有反馈回路意味着信号只能沿一个方向流动，从输入到输出。它可以分为以下两种类型 -

单层前馈网络- 该概念是前馈 ANN 仅具有一个加权层。换句话说，我们可以说输入层完全连接到输出层。

多层前馈网络- 该概念是前馈 ANN 具有多个加权层。由于该网络在输入层和输出层之间有一层或多层，因此称为隐藏层。

反馈网络

顾名思义，反馈网络具有反馈路径，这意味着信号可以使用环路在两个方向上流动。这使其成为一个非线性动态系统，不断变化直至达到平衡状态。它可以分为以下类型 -

循环网络- 它们是具有闭环的反馈网络。以下是两种类型的循环网络。
完全循环网络- 它是最简单的神经网络架构，因为所有节点都连接到所有其他节点，并且每个节点都充当输入和输出。

Jordan 网络- 它是一个闭环网络，其中输出将作为反馈再次进入输入，如下图所示。

权重或学习的调整

人工神经网络中的学习是修改指定网络神经元之间连接权重的方法。ANN 中的学习可以分为三类，即监督学习、无监督学习和强化学习。

监督学习

顾名思义，这种类型的学习是在老师的监督下完成的。这个学习过程是依赖的。

在监督学习下训练人工神经网络期间，输入向量被提供给网络，网络将给出输出向量。将该输出向量与所需的输出向量进行比较。如果实际输出与所需输出矢量之间存在差异，则会生成误差信号。根据该误差信号，调整权重，直到实际输出与期望输出匹配。

无监督学习

顾名思义，这种类型的学习是在没有老师监督的情况下完成的。这个学习过程是独立的。

在无监督学习下训练 ANN 时，相似类型的输入向量被组合起来形成簇。当应用新的输入模式时，神经网络给出输出响应，指示输入模式所属的类别。

环境没有反馈关于期望的输出是什么以及它是否正确。因此，在这种类型的学习中，网络本身必须从输入数据中发现模式和特征，以及输入数据与输出之间的关系。

强化学习

顾名思义，这种类型的学习用于强化或加强针对某些批评信息的网络。这个学习过程类似于监督学习，但是我们的信息可能非常少。

在强化学习下的网络训练过程中，网络会收到来自环境的一些反馈。这使得它有点类似于监督学习。然而，这里获得的反馈是评估性的而不是指导性的，这意味着监督学习中没有老师。收到反馈后，网络会调整权重，以便将来获得更好的批评者信息。

激活函数

它可以定义为为获得精确输出而对输入施加的额外力或努力。在人工神经网络中，我们还可以对输入应用激活函数以获得准确的输出。以下是一些感兴趣的激活函数 -

线性激活函数

它也称为恒等函数，因为它不执行输入编辑。它可以定义为 -

F (x) = x

$F(x)\:=\:x$

S 形激活函数

它有两种类型，如下 -

二元 sigmoidal 函数- 此激活函数执行 0 和 1 之间的输入编辑。它本质上是积极的。它总是有界的，这意味着它的输出不能小于 0 且不能大于 1。它本质上也是严格递增的，这意味着输入越多，输出就越高。它可以定义为

$F (x) = s i g m (x) = 1 1 + e x p ( - x )$ $F(x)\:=\:sigm(x)\:=\:\frac{1}{1\:+\:exp(-x)}$
双极 S 形函数- 此激活函数在 -1 和 1 之间执行输入编辑。它本质上可以是正数或负数。它总是有界的，这意味着它的输出不能小于-1也不能大于1。它本质上也像sigmoid函数一样严格递增。它可以定义为

$F (x) = s i g m (x) = 2 1 + e x p ( - x ) - 1 = 1 - e x p ( x ) 1 + e x p ( x )$ $F(x)\:=\:sigm(x)\:=\:\frac{2}{1\:+\:exp(-x)}\:-\:1\:=\:\frac{1\:-\:exp(x)}{1\:+\:exp(x)}$

学习与适应

如前所述，ANN 完全受到生物神经系统（即人脑）工作方式的启发。人脑最令人印象深刻的特征是学习，因此人工神经网络也具有相同的特征。

人工神经网络中的学习是什么？

基本上，学习意味着当环境发生变化时，进行并适应自身的变化。ANN是一个复杂的系统，或者更准确地说，我们可以说它是一个复杂的自适应系统，它可以根据通过它的信息来改变其内部结构。

它为什么如此重要？

作为一个复杂的自适应系统，人工神经网络中的学习意味着处理单元能够随着环境的变化而改变其输入/输出Behave。当构建特定网络时，由于固定的激活函数以及输入/输出向量，人工神经网络中学习的重要性会增加。现在要改变输入/输出Behave，我们需要调整权重。

分类

它可以被定义为通过寻找同一类样本之间的共同特征来学习将样本数据区分为不同类的过程。例如，为了进行人工神经网络的训练，我们有一些具有独特特征的训练样本，而为了进行其测试，我们有一些具有其他独特特征的测试样本。分类是监督学习的一个例子。

神经网络学习规则

我们知道，在ANN学习过程中，为了改变输入/输出Behave，我们需要调整权重。因此，需要一种可以修改权重的方法。这些方法称为学习规则，它们只是算法或方程。以下是神经网络的一些学习规则 -

赫布学习规则

这条规则是最古老、最简单的规则之一，由 Donald Hebb 在 1949 年的《Behave组织》一书中提出。它是一种前馈、无监督学习。

基本概念- 该规则基于 Hebb 提出的提案，他写道 -

“当细胞 A 的轴突足够接近以激发细胞 B 并重复或持续地参与激发它时，一个或两个细胞中会发生一些生长过程或代谢变化，从而使 A 的效率成为激发 B 的细胞之一，增加了。”

根据上述假设，我们可以得出结论，如果两个神经元同时放电，则两个神经元之间的连接可能会加强，如果它们在不同时间放电，则可能会减弱。

数学公式- 根据赫布学习规则，以下是在每个时间步增加连接权重的公式。

TutorialSpoint在线教程 var _hmt = _hmt || []; (function() { var hm = document.createElement("script"); hm.src = "https://hm.baidu.com/hm.js?efc4776c9c7ca99a32f7c255829fe265"; var s = document.getElementsByTagName("script")[0]; s.parentNode.insertBefore(hm, s); })();