图论 - 基本属性
图具有各种属性,根据图的结构可用于表征图。这些属性是用与图论领域相关的特定术语定义的。在本章中,我们将讨论所有图中常见的一些基本属性。
两个顶点之间的距离
它是顶点 U 和顶点 V 之间的最短路径中的边数。如果有多个路径连接两个顶点,则最短路径被认为是两个顶点之间的距离。
符号 - d(U,V)
从一个顶点到另一顶点可以存在任意数量的路径。其中,您只需选择最短的一个。
例子
看一下下图 -
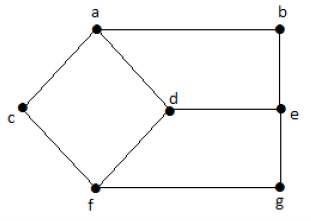
这里,从顶点“d”到顶点“e”或简单的“de”的距离是 1,因为它们之间有一条边。从顶点“d”到顶点“e”有很多路径 -
- 达、ab、是
- df、fg、ge
- de(考虑顶点之间的距离)
- df、fc、ca、ab、be
- da、ac、cf、fg、ge
顶点的偏心率
一个顶点到所有其他顶点之间的最大距离被视为顶点的偏心率。
符号 - e(V)
计算图中从特定顶点到所有其他顶点的距离,在这些距离中,偏心率是最大的距离。
例子
在上图中,“a”的偏心率为 3。
从'a'到'b'的距离是1('ab'),
从 'a' 到 'c' 是 1 ('ac'),
从'a'到'd'是1('ad'),
从'a'到'e'是2('ab'-'be')或('ad'-'de'),
从'a'到'f'是2('ac'-'cf')或('ad'-'df'),
从'a'到'g'是3('ac'-'cf'-'fg')或('ad'-'df'-'fg')。
因此,偏心率为 3,这是从顶点“a”到“ag”之间距离的最大值。
换句话说,
e(b) = 3
e(c) = 3
e(d) = 2
e(e) = 3
e(f) = 3
e(g) = 3
连通图的半径
所有顶点的最小偏心率被视为图 G 的半径。一个顶点到所有其他顶点之间的所有最大距离中的最小值被视为图 G 的半径。
符号 - r(G)
根据图中顶点的所有偏心率,连通图的半径是所有这些偏心率中的最小值。
例子
在上图中,r(G) = 2,这是“d”的最小偏心率。
图的直径
所有顶点的最大偏心率被视为图 G 的直径。一个顶点到所有其他顶点之间的所有距离中的最大值被视为图 G 的直径。
符号 - d(G) - 从图中顶点的所有偏心率中,连通图的直径是所有这些偏心率中的最大值。
例子
上图中,d(G) = 3;这是最大偏心率。
中心点
如果图形的偏心率等于其半径,则该点称为图形的中心点。如果
e(V) = r(V),
那么“V”是图“G”的中心点。
例子
在示例图中,“d”是图的中心点。
e(d) = r(d) = 2
中心
“G”的所有中心点的集合称为图的中心。
例子
在示例图表中,{'d'} 是图表的中心。
圆周
“G”的最长周期中的边数称为“G”的周长。
例子
在示例图中,周长为 6,这是我们从最长周期 acfgeba 或 acfdeba 得出的。
周长
“G”的最短周期中的边数称为其周长。
符号: g(G)。
示例- 在示例图中,图的周长为 4,我们从最短周期 acfda 或 dfged 或 abeda 得出。
顶点度数总和定理
如果 G = (V, E) 是一个无向图,顶点为 V = {V 1 , V 2 ,…V n } 则
推论1
如果 G = (V, E) 是顶点为 V = {V 1 , V 2 ,…V n } 的有向图,则
推论2
在任意无向图中,奇数度的顶点个数为偶数。
推论3
在无向图中,如果每个顶点的度为k,则
推论4
在无向图中,如果每个顶点的度至少为k,则
| 推论5
在无向图中,如果每个顶点的度至多为k,则
