图论 - 快速指南

图论 - 简介

在数学和计算机科学领域，图论是对涉及边和顶点之间关系的图的研究。它是一门热门学科，在计算机科学、信息技术、生物科学、数学和语言学等领域都有应用。话不多说，让我们从定义一个图开始。

什么是图表？

图表是一组对象的图形表示，其中一些对象对通过链接连接。互连的对象由称为顶点的点表示，连接顶点的链接称为边。

形式上，图是一对集合(V, E)，其中V是顶点集合，E 是连接顶点对的边集合。看一下下图 -

顶点对

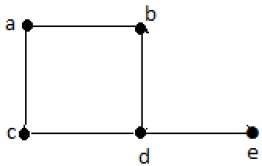
在上图中，

V = {a, b, c, d, e}

E = {ab, ac, bd, cd, de}

图论的应用

图论在工程的各个领域都有其应用 -

电气工程- 图论的概念广泛用于设计电路连接。连接的类型或组织被称为拓扑。拓扑的一些示例是星形、桥式、串联和并联拓扑。

计算机科学- 图论用于算法的研究。例如，

  • 克鲁斯卡尔算法
  • 普里姆算法
  • 迪杰斯特拉算法

计算机网络- 网络中互连计算机之间的关系遵循图论原理。

科学- 物质的分子结构和化学结构、生物体的 DNA 结构等通过图表表示。

语言学- 语言的解析树和语言的语法使用图。

一般- 城市之间的路线可以使用图表来表示。描述层次有序信息（例如家谱）可以用作称为树的特殊类型的图。

图论 - 基础知识

图形是由点和连接到这些点的线组成的图。它至少有一条线连接一组两个顶点，没有顶点连接自身。图论中图的概念建立在一些基本术语上，例如点、线、顶点、边、顶点度、图的属性等。在本章中，我们将介绍图论的这些基础知识。

观点

点是一维、二维或三维空间中的特定位置。为了更好地理解，可以用字母表来表示点。可以用点来表示。

例子

观点

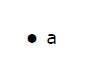
这里，点是一个名为“a”的点。

线

线是两点之间的连接。可以用实线来表示。

例子

线

这里，“a”和“b”是点。这两点之间的连接称为线。

顶点

顶点是多条线相交的点。它也称为节点。与点类似，顶点也用字母表示。

例子

顶点

这里，顶点以字母“a”命名。

边缘

边是连接两个顶点的线的数学术语。许多边可以由单个顶点形成。没有顶点，就无法形成边。边必须有起始顶点和结束顶点。

例子

边缘

这里，“a”和“b”是两个顶点，它们之间的连接称为边。

图形

图“G”定义为 G = (V, E)，其中 V 是图中所有顶点的集合，E 是图中所有边的集合。

实施例1

图形

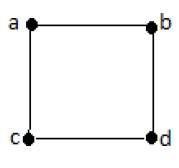
在上面的示例中，ab、ac、cd 和 bd 是图的边。类似地，a、b、c 和 d 是图的顶点。

实施例2

图的顶点

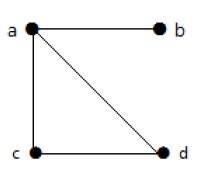
在此图中，有四个顶点 a、b、c 和 d，以及四个边 ab、ac、ad 和 cd。

环形

在图中，如果从顶点到自身绘制一条边，则称为环。

实施例1

环形

在上图中，V 是一个顶点，它有一条形成环的边 (V, V)。

实施例2

两个循环

在此图中，在顶点 a 和顶点 b 处形成两个环。

顶点度数

它是与顶点 V 相邻的顶点数。

符号- deg(V)。

在具有 n 个顶点的简单图中，任何顶点的度数为 -

deg(v) ≤ n – 1 ∀ v ∈ G

一个顶点可以与除自身以外的所有其他顶点形成边。因此，顶点的度数将最多为图中的顶点数减 1。这个 1 用于自顶点，因为它本身不能形成循环。如果任何顶点处存在环，则它不是简单图。

顶点的度数可以在图的两种情况下考虑 -

  • 无向图

  • 有向图

无向图中顶点的度数

无向图没有有向边。考虑以下示例。

实施例1

看一下下图 -

无向图

在上面的无向图中，

  • deg(a) = 2，因为有 2 条边在顶点“a”处相交。

  • deg(b) = 3，因为有 3 条边在顶点“b”处相交。

  • deg(c) = 1，因为在顶点“c”处形成 1 条边

  • 所以'c'是一个下垂的顶点。

  • deg(d) = 2，因为有 2 条边在顶点“d”处相交。

  • deg(e) = 0，因为在顶点“e”处形成了 0 条边。

  • 所以 'e' 是一个孤立的顶点。

实施例2

看一下下图 -

顶点度数

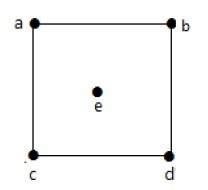
在上图中，

deg(a) = 2、deg(b) = 2、deg(c) = 2、deg(d) = 2 以及 deg(e) = 0。

顶点“e”是孤立顶点。该图没有任何悬垂顶点。

有向图中顶点的度数

在有向图中，每个顶点都有一个入度和一个出度。

图的入度

  • 顶点 V 的入度是进入顶点 V 的边的数量。

  • 符号-deg-(V)。

图的出度

  • 顶点V的出度是从顶点V出去的边的数量。

  • 符号- deg+(V)。

考虑以下示例。

实施例1

看看下面的有向图。顶点“a”有两条边“ad”和“ab”，它们向外延伸。因此它的出度是 2。类似地，有一条边“ga”，朝向顶点“a”。因此'a'的入度是1。

有向图

其他顶点的入度和出度如下表所示 -

顶点 入度 出度
A 1 2
乙 2 0
C 2 1
d 1 1
e 1 1
F 1 1
G 0 2

实施例2

看看下面的有向图。顶点“a”具有从顶点“a”向外延伸的边“ae”。因此，它的出度是 1。类似地，该图有一条边“ba”朝向顶点“a”。因此'a'的入度是1。

入度和出度

其他顶点的入度和出度如下表所示 -

顶点 入度 出度
A 1 1
乙 0 2
C 2 0
d 1 1
e 1 1

下垂顶点

通过使用顶点的度数，我们有两种特殊类型的顶点。度数为 1 的顶点称为下垂顶点。

例子

下垂顶点

这里，在此示例中，顶点“a”和顶点“b”具有连接的边“ab”。因此，对于顶点“a”，仅存在一条朝向顶点“b”的边，并且类似地，对于顶点“b”，仅存在朝向顶点“a”的一条边。最后，顶点'a'和顶点'b'具有相同的度数，也称为下垂顶点。

孤立的顶点

度数为零的顶点称为孤立顶点。

例子

孤立的顶点.jpg

这里，顶点“a”和顶点“b”彼此之间以及与任何其他顶点之间没有连接。因此顶点 'a' 和 'b' 的度数均为零。这些也称为孤立顶点。

邻接

以下是邻接规范 -

  • 在图中，如果两个顶点之间存在边，则称两个顶点是相邻的。在这里，顶点的相邻性由连接这两个顶点的单边维持。

  • 在图中，如果两条边之间存在公共顶点，则称两条边相邻。这里，边的相邻性由连接两条边的单个顶点来维持。

实施例1

邻接

在上图中 -

  • “a”和“b”是相邻顶点，因为它们之间有公共边“ab”。

  • “a”和“d”是相邻顶点，因为它们之间有公共边“ad”。

  • ab' 和 'be' 是相邻边，因为它们之间有一个公共顶点 'b'。

  • be' 和 'de' 是相邻边，因为它们之间有一个公共顶点 'e'。

实施例2

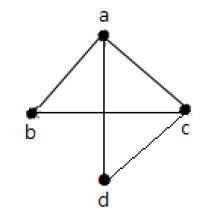
相邻顶点和相邻边

在上图中 -

  • “a”和“d”是相邻顶点，因为它们之间有公共边“ad”。

  • “c”和“b”是相邻顶点，因为它们之间有公共边“cb”。

  • “ad”和“cd”是相邻边，因为它们之间有一个公共顶点“d”。

  • “ac”和“cd”是相邻边，因为它们之间有一个公共顶点“c”。

平行边

在图中，如果一对顶点由多条边连接，则这些边称为平行边。

平行边

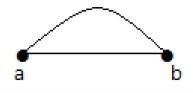
在上图中，“a”和“b”是两个顶点，它们之间通过两条边“ab”和“ab”连接。因此它被称为平行边。

多图

具有平行边的图称为多重图。

实施例1

多图

在上图中，有五个边“ab”、“ac”、“cd”、“cd”和“bd”。由于“c”和“d”之间有两条平行边，因此它是一个多重图。

实施例2

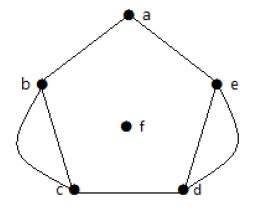
两条边多重图

在上图中，顶点“b”和“c”有两条边。顶点“e”和“d”之间也有两条边。因此它是一个多重图。

图的度数列

如果将图中所有顶点的度按降序或升序排列，则得到的序列称为该图的度序列。

实施例1

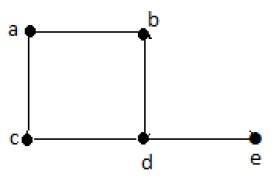
图的度数列
顶点 A 乙 C d e
正在连接到 公元前 广告 广告 c、b、e d
程度 2 2 2 3 1

在上图中，对于顶点{d,a,b,c,e}，度数序列为{3,2,2,2,1}。

实施例2

学位序列
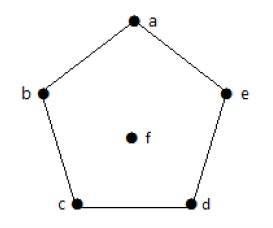
顶点 A 乙 C d e F
正在连接到 是 一个,c 乙、丁 丙、乙 广告 -
程度 2 2 2 2 2 0

在上图中，对于顶点{a,b,c,d,e,f}，度数序列为{2,2,2,2,2,0}。

图论 - 基本属性

图具有各种属性，根据图的结构可用于表征图。这些属性是用与图论领域相关的特定术语定义的。在本章中，我们将讨论所有图中常见的一些基本属性。

两个顶点之间的距离

它是顶点 U 和顶点 V 之间的最短路径中的边数。如果有多个路径连接两个顶点，则最短路径被认为是两个顶点之间的距离。

符号 - d(U,V)

从一个顶点到另一顶点可以存在任意数量的路径。其中，您只需选择最短的一个。

例子

看一下下图 -

两个顶点

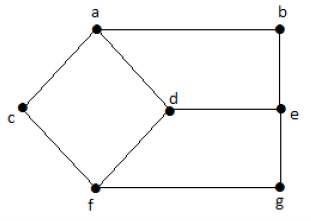
这里，从顶点“d”到顶点“e”或简单的“de”的距离是 1，因为它们之间有一条边。从顶点“d”到顶点“e”有很多路径 -

  • 达、ab、是
  • df、fg、ge
  • de（考虑顶点之间的距离）
  • df、fc、ca、ab、be
  • da、ac、cf、fg、ge

顶点的偏心率

一个顶点到所有其他顶点之间的最大距离被视为顶点的偏心率。

符号 - e(V)

计算图中从特定顶点到所有其他顶点的距离，在这些距离中，偏心率是最大的距离。

例子

在上图中，“a”的偏心率为 3。

从'a'到'b'的距离是1（'ab'），

从 'a' 到 'c' 是 1 ('ac')，

从'a'到'd'是1（'ad'），

从'a'到'e'是2（'ab'-'be'）或（'ad'-'de'），

从'a'到'f'是2（'ac'-'cf'）或（'ad'-'df'），

从'a'到'g'是3（'ac'-'cf'-'fg'）或（'ad'-'df'-'fg'）。

因此，偏心率为 3，这是从顶点“a”到“ag”之间距离的最大值。

换句话说，

e(b) = 3

e(c) = 3

e(d) = 2

e(e) = 3

e(f) = 3

e(g) = 3

连通图的半径

所有顶点的最小偏心率被视为图 G 的半径。一个顶点到所有其他顶点之间的所有最大距离中的最小值被视为图 G 的半径。

符号 - r(G)

根据图中顶点的所有偏心率，连通图的半径是所有这些偏心率中的最小值。

例子

在上图中，r(G) = 2，这是“d”的最小偏心率。

图的直径

所有顶点的最大偏心率被视为图 G 的直径。一个顶点到所有其他顶点之间的所有距离中的最大值被视为图 G 的直径。

符号 - d(G) - 从图中顶点的所有偏心率中，连通图的直径是所有这些偏心率中的最大值。

例子

上图中，d(G) = 3；这是最大偏心率。

中心点

如果图形的偏心率等于其半径，则该点称为图形的中心点。如果

e(V) = r(V),

那么“V”是图“G”的中心点。

例子

在示例图中，“d”是图的中心点。

e(d) = r(d) = 2

中心

“G”的所有中心点的集合称为图的中心。

例子

在示例图表中，{'d'} 是图表的中心。

圆周

“G”的最长周期中的边数称为“G”的周长。

例子

在示例图中，周长为 6，这是我们从最长周期 acfgeba 或 acfdeba 得出的。

周长

“G”的最短周期中的边数称为其周长。

符号： g(G)。

示例- 在示例图中，图的周长为 4，我们从最短周期 acfda 或 dfged 或 abeda 得出。

顶点度数总和定理

如果 G = (V, E) 是一个无向图，顶点为 V = {V 1 , V 2 ,…V n } 则

n Σ i=1 deg(V i ) = 2|E|

推论1

如果 G = (V, E) 是顶点为 V = {V 1 , V 2 ,…V n } 的有向图，则

n Σ i=1 deg+(V i ) = |E| = n Σ i=1 deg−(V i )

推论2

在任意无向图中，奇数度的顶点个数为偶数。

推论3

在无向图中，如果每个顶点的度为k，则

k|V| = 2|E|

推论4

在无向图中，如果每个顶点的度至少为k，则

k|V| ≤ 2|E|

| 推论5

在无向图中，如果每个顶点的度至多为k，则

k|V| ≥ 2|E|

图论 - 图的类型

根据顶点数量、边数量、互连性及其整体结构，图有多种类型。本章中我们将仅讨论某些重要的图表类型。

空图

没有边的图称为空图。

例子

空图

在上图中，有三个名为“a”、“b”和“c”的顶点，但它们之间没有边。因此它是一个空图。

简单图

只有一个顶点的图称为平凡图。

例子

顶点

在上图中，只有一个顶点“a”，没有其他边。因此它是一个平凡图。

无向图

无向图包含边，但边不是有向的。

例子

无向图

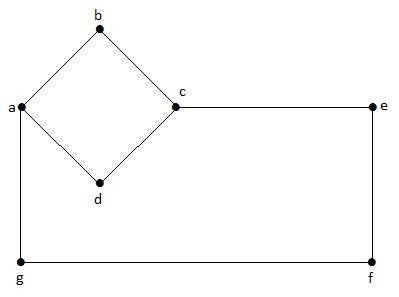
在此图中，'a'、'b'、'c'、'd'、'e'、'f'、'g' 是顶点，'ab'、'bc'、'cd'、'da '、'ag'、'gf'、'ef' 是图的边。由于它是无向图，因此边“ab”和“ba”相同。类似地，其他边也以同样的方式考虑。

有向图

在有向图中，每条边都有一个方向。

例子

有向图

在上图中，我们有七个顶点 'a'、'b'、'c'、'd'、'e'、'f' 和 'g'，以及八条边 'ab'、'cb'、' dc'、'ad'、'ec'、'fe'、'gf' 和 'ga'。由于它是有向图，因此每条边都有一个显示其方向的箭头标记。请注意，在有向图中，“ab”与“ba”不同。

简单图

没有环且没有平行边的图称为简单图。

  • 具有“n”个顶点的单个图中可能的最大边数为n C 2，其中n C 2 = n(n – 1)/2。

  • 具有“n”个顶点的简单图的数量 = 2 n c 2 = 2 n(n-1)/2。

例子

在下图中，有 3 个顶点和 3 条边，这是最大的，不包括平行边和环。这可以用上面的公式来证明。

简单图

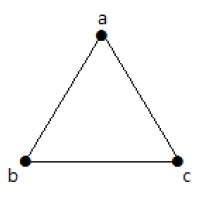
n=3 个顶点的最大边数 -

n C 2 = n(n–1)/2

= 3(3–1)/2

= 6/2

= 3 条边

n=3 个顶点的简单图的最大数量 -

2 n C 2 = 2 n(n-1)/2

= 2 3(3-1)/2

= 2 3

8

这 8 个图表如下所示 -

简单图的最大数量

连通图

如果每对顶点之间都存在路径，则称图 G 是连通的。图中的每个顶点都应该至少有一条边。这样我们就可以说它连接到边另一侧的某个其他顶点。

例子

在下图中，每个顶点都有自己的边连接到其他边。因此它是一个连通图。

连通图

断开的图

如果图 G 不包含至少两个连接的顶点，则该图 G 是断开连接的。

实施例1

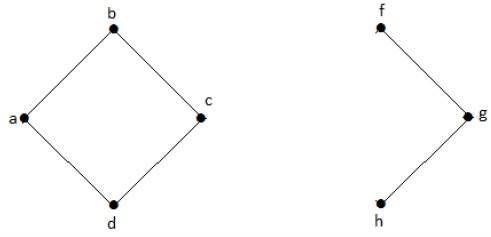
下图是断开图的示例，其中有两个组件，一个具有“a”、“b”、“c”、“d”顶点，另一个具有“e”、“f”、“g”， 'h' 顶点。

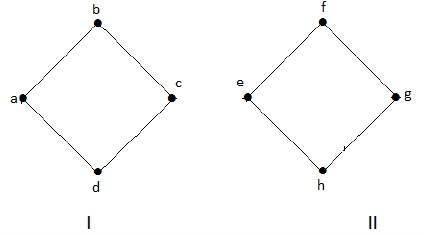
独立断开图

这两个组件是独立的并且彼此不连接。因此它被称为断开图。

实施例2

两个独立的组件

在此示例中，有两个独立的组件 abfe 和 cd，它们彼此不相连。因此这是一个断开连接的图。

正则图

如果图 G 的所有顶点都具有相同的度数，则称图 G 是正则图。在图中，如果每个顶点的度为“k”，则该图称为“k-正则图”。

例子

在下图中，所有顶点都具有相同的度数。所以这些图称为正则图。

正则图

在这两个图中，所有顶点的度数都是 2。它们被称为 2-正则图。

完整图

具有“n”个相互顶点的简单图称为完全图，用“K n ”表示。图中，一个顶点与其他所有顶点都应该有边，则称为完全图。

换句话说，如果一个顶点与图中的所有其他顶点相连，则称为完全图。

例子

在下图中，图中的每个顶点都与图中除自身之外的所有其余顶点相连。

完整图表

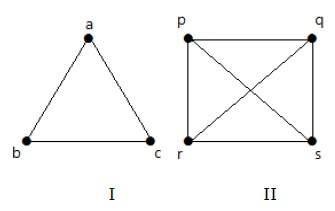
在图一中，

A 乙 C
A 未连接 连接的 连接的
乙 连接的 未连接 连接的
C 连接的 连接的 未连接

在图二中，

p q r s
p 未连接 连接的 连接的 连接的
q 连接的 未连接 连接的 连接的
r 连接的 连接的 未连接 连接的
s 连接的 连接的 连接的 未连接

循环图

具有“n”个顶点（n >= 3）和“n”条边的简单图，如果其所有边形成长度为“n”的循环，则称为循环图。

如果图中每个顶点的度为二，则称为循环图。

符号- C n

例子

看看下面的图表 -

  • 图 I 有 3 个顶点和 3 条边，形成一个循环“ab-bc-ca”。

  • 图 II 有 4 个顶点和 4 条边，形成一个循环“pq-qs-sr-rp”。

  • 图 III 有 5 个顶点和 5 条边，形成一个循环“ik-km-ml-lj-ji”。

循环图

因此所有给定的图都是循环图。

轮图

循环图C n-1通过添加新的顶点得到轮图。该新顶点称为Hub ，它连接到 C n的所有顶点。

符号 - W n

W 中的边数n = 从中心到所有其他顶点的边数 +

循环图中没有中心的所有其他节点的边数。

= (n–1) + (n–1)

= 2(n–1)

例子

看看下面的图表。它们都是轮图。

轮图

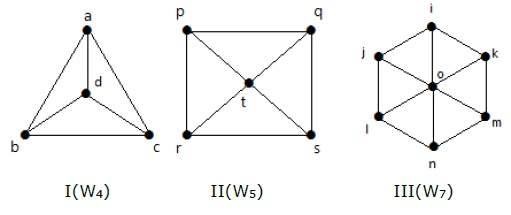
在图I中，它是通过在中间添加一个名为“d”的顶点从C 3获得的。其被表示为W 4。

W4 中的边数 = 2(n-1) = 2(3) = 6

在图II中，它是通过在中间添加一个名为“t”的顶点从C4获得的。其被表示为W 5。

W5 中的边数 = 2(n-1) = 2(4) = 8

在图III中，它是通过在中间添加一个名为“o”的顶点从C 6获得的。其被表示为W 7。

W4 中的边数 = 2(n-1) = 2(6) = 12

循环图

至少有一个环的图称为循环图。

例子

循环图

在上面的示例图中，我们有两个循环 abcda 和 cfgec。因此它被称为循环图。

非循环图

没有环的图称为无环图。

例子

非循环图

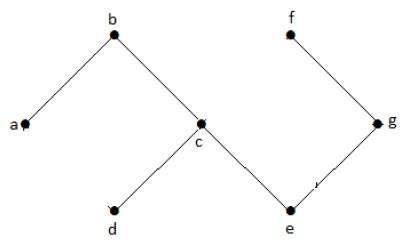
在上面的示例图中，我们没有任何循环。因此它是一个非循环图。

二分图

如果 E 的每条边将 V1 中的一个顶点连接到 V 2 中的一个顶点，则具有顶点划分 V = {V 1 , V 2 }的简单图 G = (V, E ) 称为二部图。

一般来说，Bipertite 图有两组顶点，比如说 V1 和 V2，如果绘制一条边，它应该将集合 V 1 中的任何顶点连接到集合V 2 中的任何顶点。

例子

二分图

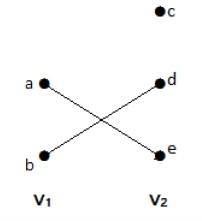
在此图中，您可以观察两组顶点 - V 1和 V 2。这里，名为“ae”和“bd”的两条边连接两个集合V 1和V 2的顶点。

完全二分图

如果 V 1中的每个顶点都连接到 V 2 中的每个顶点，则具有分区 V = {V 1 , V 2 } 的二部图' G'，G = (V, E)被称为完全二部图。

一般来说，完整的二部图将集合 V 1中的每个顶点连接到集合 V 2中的每个顶点。

例子

下图是完全二分图，因为它具有将集合 V 1中的每个顶点连接到集合 V 2中的每个顶点的边。

完全二分图

如果 |V 1 | = m 和 |V 2 | = n，则完全二分图记为 K m, n。

  • K m,n有 (m+n) 个顶点和 (mn) 个边。
  • 如果 m=n， K m,n是正则图。

一般来说，完全二部图不是完全图。

如果 m=n=1， K m,n是完全图。

具有 n 个顶点的二部图中的最大边数为 -

[n 2 /4]

如果n=10，k5,5=[n2/4]=[10 2 /4]=25。

同理，K6,4=24

K7、3=21

K8，2=16

K9，1=9

如果 n=9, k5, 4 = [n2/4] = [92/4] = 20

同理，K6,3=18

K7、2=14

K8，1=8

如果“G”没有奇数长度的环，则“G”是二分图。二部图的一个特例是星图。

星图

K1, n-1 形式的完全二部图是具有 n 个顶点的星图。如果单个顶点属于一个集合并且所有剩余顶点属于另一个集合，则星图是完全二部图。

例子

星图

在上图中，在“n”个顶点中，所有“n–1”个顶点都连接到单个顶点。因此它的形式为K 1 , n-1，即星图。

图的补集

设'G−'是一个简单图，其中一些顶点与'G'相同，并且边{U, V}存在于'G−'中，如果边不存在于G中。这意味着，两个顶点是相邻的在 'G−' 中，如果两个顶点在 G 中不相邻。

如果图 I 中存在的边在另一个图 II 中不存在，并且图 I 和图 II 组合在一起形成完整图，则图 I 和图 II 称为互补图。

例子

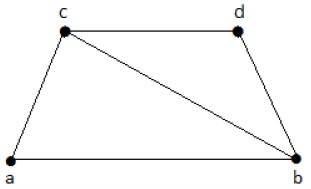
在下面的示例中，图 I 有两条边“cd”和“bd”。它的补图-II 有四个边。

图的补集

请注意，图 I 中的边不存在于图 II 中，反之亦然。因此，两个图的组合给出了“n”个顶点的完整图。

注意- 两个互补图的组合给出一个完整的图。

如果“G”是任何简单图，那么

|E(G)| + |E('G-')| = |E(Kn)|，其中 n = 图中的顶点数。

例子

设“G”是一个有九个顶点和十二条边的简单图，求“G-”中边的数量。

你有，|E(G)| + |E('G-')| = |E(Kn)|

12 + |E('G-')| =

9(9-1) / 2 = 9 C 2

12 + |E('G-')| = 36

|E('G-')| = 24

'G' 是一个有 40 条边的简单图，它的补图 'G−' 有 38 条边。求图 G 或 'G−' 中的顶点数。

设图中的顶点数为“n”。

我们有，|E(G)| + |E('G-')| = |E(Kn)|

40 + 38 = n(n-1)/2

156 = n(n-1)

13(12) = n(n-1)

n = 13

图论 - 树

树是甚至不包含单个循环的图。它们以图形形式表示层次结构。树属于最简单的图类。尽管它们很简单，但它们具有丰富的结构。

树提供了一系列有用的应用程序，从简单的家谱到复杂的计算机科学数据结构中的树。

树

连接的无环图称为树。换句话说，没有环的连通图称为树。

树的边缘称为分支。树的元素称为节点。没有子节点的节点称为叶节点。

具有“n”个顶点的树有“n-1”条边。如果它比“n-1”多一条边，那么额外的边显然必须与两个顶点配对，从而形成一个循环。然后，它就变成了循环图，这违反了树图。

实施例1

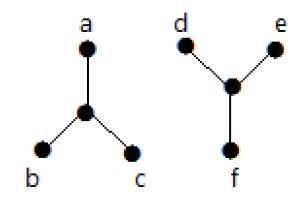
这里显示的图是一棵树，因为它没有循环并且是相连的。它有四个顶点和三个边，即定义中提到的“n”个顶点有“n-1”条边。

树

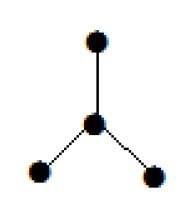
注意- 每棵树至少有两个一级顶点。

实施例2

一的程度。

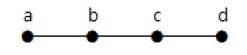
在上面的示例中，顶点“a”和“d”的度数为 1。另外两个顶点 'b' 和 'c' 的度数为 2。这是可能的，因为为了不形成环，图中的任何位置都应该至少有两个单边。它只不过是两条度数为 1 的边。

森林

断开的无环图称为森林。换句话说，不相交的树木集合称为森林。

例子

下图看起来像两个子图；但它是一个单独的断开连接的图。该图中没有循环。因此，显然这是一片森林。

森林

生成树

设 G 是连通图，则 G 的子图 H 称为 G 的生成树，如果 -

  • H是一棵树
  • H包含G的所有顶点。

无向图 G 的生成树 T 是包含 G 的所有顶点的子图。

例子

生成树

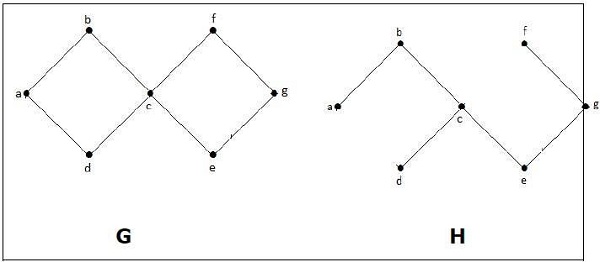
在上面的例子中，G是连通图，H是G的子图。

显然，图H没有环，它是一棵有6条边的树，边数比总顶点数少1条。因此H是G的生成树。

电路等级

设“G”为具有“n”个顶点和“m”条边的连通图。G 的生成树“T”包含 (n-1) 条边。

因此，为了得到生成树，需要从“G”中删除的边数 = m-(n-1)，称为 G 的电路秩。

这个公式是正确的，因为在生成树中你需要有“n-1”条边。在“m”条边中，您需要在图中保留“n–1”条边。

因此，从“m”中删除“n–1”条边会给出从图中删除的边，以便获得生成树，该生成树不应形成循环。

例子

看一下下图 -

电路等级

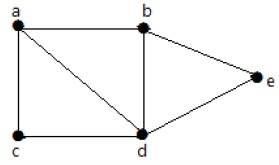
对于上面示例中给出的图，有 m=7 个边和 n=5 个顶点。

那么电路等级是 -

G = m – (n – 1)

= 7 – (5 – 1)

= 3

例子

令“G”为具有六个顶点的连通图，每个顶点的度数为三。求“G”的电路等级。

由顶点度和定理，

n Σ i=1 deg(V i ) = 2|E|

6 × 3 = 2|E|

|E| = 9

电路等级 = |E| – (|V| – 1)

= 9 – (6 – 1) = 4

基尔霍夫定理

基尔霍夫定理对于查找可从连通图形成的生成树的数量非常有用。

例子

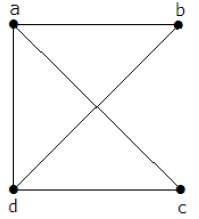
基尔霍夫定理

矩阵“A”填充为，如果两个顶点之间有一条边，则应将其指定为“1”，否则应指定为“0”。

$$A=\begin{vmatrix}0 & a & b & c & d\\a & 0 & 1 & 1 & 1 \\b & 1 & 0 & 0 & 1\\c & 1 & 0 & 0 & 1\\d & 1 & 1 & 1 & 0 \end{vmatrix} = \begin{vmatrix} 0 & 1 & 1 & 1\\1 & 0 & 0 & 1\\1 & 0 & 0 & 1\\ 1 & 1 & 1 & 0\end{vmatrix}$$

根据基尔霍夫定理，应改为将主对角线值替换为顶点的度数，并将所有其他元素替换为-1.A

$$=\begin{vmatrix} 3 & -1 & -1 & -1\\-1 & 2 & 0 & -1\\-1 & 0 & 2 & -1\\-1 & -1 & -1 & 3 \end{vmatrix}=M$$ $$M=\begin{vmatrix}3 & -1 & -1 & -1\\-1 & 2 & 0 & -1\\-1 & 0 & 2 & -1\\-1 & -1 & -1 & 3 \end{vmatrix} =8$$ $$Co\:\:m1\:\:= \begin{vmatrix 的因子\:\: } 2 & 0 & -1\\0 & 2 & -1\\-1 & -1 & 3\end{vmatrix}$$

因此，生成树的数量 = 8。

图论 - 连接性

是否可以将图从一个顶点遍历到另一个顶点取决于图的连接方式。连接性是图论中的一个基本概念。连接性定义了图是连接的还是断开的。它具有基于边和顶点的子主题，称为边连接性和顶点连接性。让我们详细讨论它们。

连接性

如果每对顶点之间都有路径，则称图是连通的。从每个顶点到任何其他顶点，都应该有一些路径可以遍历。这就是所谓的图的连通性。具有多个断开的顶点和边的图称为断开的。

实施例1

在下图中，可以从一个顶点移动到任何其他顶点。例如，可以使用路径“ab-e”从顶点“a”遍历到顶点“e”。

连接性

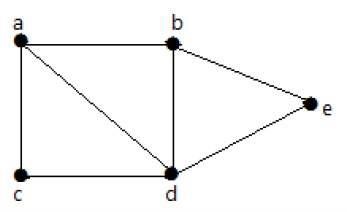
实施例2

在以下示例中，从顶点“a”遍历到顶点“f”是不可能的，因为它们之间没有直接或间接的路径。因此它是一个断开连接的图。

断开的图

剪切顶点

令“G”为连通图。如果“G-V”（从“G”中删除“V”）导致断开图，则顶点 V ∈ G 称为“G”的割顶点。从图中删除切割顶点会将其分成两个或更多图。

注意- 删除切割顶点可能会导致图形断开连接。

连通图“G”最多可以有 (n–2) 个割点。

例子

在下图中，顶点“e”和“c”是切割顶点。

剪切顶点

通过删除“e”或“c”，该图将成为断开连接的图。

剪切顶点 具有割点的断开图

如果没有“g”，顶点“c”和顶点“h”以及许多其他顶点之间就没有路径。因此，它是一个断开的图，割点为“e”。类似地，“c”也是上图的切割顶点。

切边（桥）

令“G”为连通图。如果“G-e”导致断开的图，则边“e”∈G 称为切割边。

如果删除图中的一条边会产生两个或更多图，则该边称为剪切边。

例子

在下图中，切割边缘为[(c, e)]。

剪切顶点

通过从图中删除边（c，e），它就变成了一个断开的图。

剪切顶点 图形的切边

在上图中，删除边 (c, e) 将图分成两部分，这只不过是一个断开的图。因此，边（c，e）是图的切边。

注意- 令“G”为具有“n”个顶点的连通图，然后

  • 当且仅当边“e”不是 G 中任何循环的一部分时，切边 e ∈ G。

  • 可能的最大切割边数为“n-1”。

  • 每当存在切边时，切顶点也存在，因为切边的至少一个顶点是切顶点。

  • 如果存在切割顶点，则切割边可能存在也可能不存在。

图的割集

设 'G'= (V, E) 为连通图。如果从 G 中删除 E' 的所有边使 G 断开连接，则 E 的子集 E' 称为 G 的割集。

如果从图中删除一定数量的边使其断开，则这些删除的边称为图的割集。

例子

看一下下图。其割集为 E1 = {e1, e3, e5, e8}。

图的割集

从图中删除割集 E1 后，它将显示如下 -

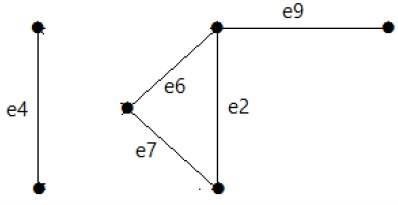
移除切割集

类似地，还有其他割集可以断开图 -

  • E3 = {e9} – 图的最小割集。

  • E4 = {e3, e4, e5}

边缘连接

令“G”为连通图。删除使“G”断开的边的最小数量称为 G 的边连通性。

符号- λ(G)

换句话说，G的最小割集中的边的数量称为G的边连通性。

如果“G”有切边，则 λ(G) 为 1。（G 的边连通性。）

例子

看一下下图。通过删除两条最小边，连通图就会断开。因此，其边缘连通性 (λ(G)) 为 2。

边缘连接

以下是通过删除两条边来断开图形的四种方法 -

删除两条边

顶点连接

令“G”为连通图。删除使“G”断开或将“G”简化为平凡图的顶点的最小数量称为其顶点连通性。

符号- K(G)

例子

在上图中，删除顶点“e”和“i”会使图断开连接。

连通图

如果 G 有割顶点，则 K(G) = 1。

符号- 对于任何连通图 G，

K(G) ≤ λ(G) ≤ δ(G)

顶点连通性 (K(G))、边连通性 (λ(G))、G 的最小度数 (δ(G))。

例子

计算下图的 λ(G) 和 K(G) -

顶点连接

解决方案

从图中可以看出，

δ(G) = 3

K(G) ≤ λ(G) ≤ δ(G) = 3 (1)

K(G)≥2 (2)

删除边{d，e}和{b，h}，我们可以断开G。

所以，

λ(G) = 2

2 ≤ λ(G) ≤ δ(G) = 2 (3)

由(2)和(3)可知，顶点连通性K(G) = 2

图论 - 覆盖

覆盖图是一个子图，它包含与其他图相对应的所有顶点或所有边。包含所有顶点的子图称为线/边覆盖。包含所有边的子图称为顶点覆盖。

线路覆盖

设 G = (V, E) 为图。如果 G 的每个顶点与 C 中的至少一条边重合，则子集 C(E) 称为 G 的线覆盖，即

deg(V) ≥ 1 ∀ V ∈ G

因为每个顶点都通过边与另一个顶点连接。因此它的最小度为 1。

例子

看一下下图 -

线路覆盖

其具有线覆盖的子图如下 -

C 1 = {{a, b}, {c, d}}

C 2 = {{a, d}, {b, c}}

C 3 = {{a, b}, {b, c}, {b, d}}

C 4 = {{a, b}, {b, c}, {c, d}}

当且仅当“G”具有孤立顶点时，“G”的线覆盖不存在。具有“n”个顶点的图的线覆盖至少有 [n/2] 条边。

最小线覆盖

如果无法从 C 中删除任何边，则称覆盖图 G 的 C 的线是最小的。

例子

在上图中，具有线覆盖的子图如下 -

C 1 = {{a, b}, {c, d}}

C 2 = {{a, d}, {b, c}}

C 3 = {{a, b}, {b, c}, {b, d}}

C 4 = {{a, b}, {b, c}, {c, d}}

这里，C 1、C 2、C 3是最小线覆盖，而 C 4不是，因为我们可以删除 {b, c}。

最小线路覆盖

它也称为最小最小线覆盖。具有最少边数的最小线覆盖称为“G”的最小线覆盖。覆盖“G”的最小线中的边数称为“G”的线覆盖数（α 1）。

例子

在上面的例子中，C 1和 C 2是 G 的最小线覆盖，且 α 1 = 2。

  • 每个线覆盖都包含一个最小线覆盖。

  • 每个线覆盖不包含最小线覆盖（C 3不包含任何最小线覆盖。

  • 最小线覆盖不包含循环。

  • 如果覆盖“C”的线不包含长度为 3 或以上的路径，则“C”是最小线覆盖，因为“C”的所有组件都是星形图，并且从星形图中不能删除任何边。

顶点覆盖

让 'G' = (V, E) 成为一个图。如果“G”的每条边都与“K”中的顶点重合或被“K”中的顶点覆盖，则 V 的子集 K 称为“G”的顶点覆盖。

例子

看一下下图 -

顶点覆盖

从上图可以得出的子图如下 -

K 1 = {b, c}

K 2 = {a, b, c}

K 3 = {b,c,d}

K 4 = {a, d}

这里，K 1、K 2和K 3具有顶点覆盖，而K 4没有任何顶点覆盖，因为它不覆盖边{bc}。

最小顶点覆盖

如果没有顶点可以从“K”中删除，则图“G”的顶点“K”被称为最小顶点覆盖。

例子

在上图中，具有顶点覆盖的子图如下 -

K 1 = {b, c}

K 2 = {a, b, c}

K 3 = {b,c,d}

这里，K 1和K 2是最小顶点覆盖，而在K 3中，顶点“d”可以被删除。

最小顶点覆盖

它也被称为最小最小顶点覆盖。具有最少顶点数的图“G”的最小顶点覆盖称为最小顶点覆盖。

“G”的最小顶点覆盖中的顶点数称为G的顶点覆盖数(α 2 )。

例子

在下图中，具有顶点覆盖的子图如下 -

K 1 = {b, c}

K 2 = {a, b, c}

K 3 = {b,c,d}

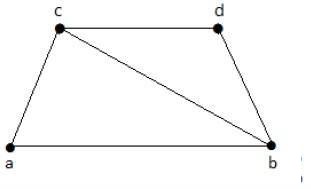
最小顶点覆盖

这里，K 1是G的最小顶点覆盖，因为它只有两个顶点。α 2 = 2。

图论 - 匹配

匹配图是图的子图，其中没有彼此相邻的边。简单地说，任何两条边之间不应该有任何公共顶点。

匹配

让 'G' = (V, E) 成为一个图。如果 G 的每个顶点最多与 M 中的一条边重合，则子图称为匹配 M(G) ，即

deg(V) ≤ 1 ∀ V ∈ G

这意味着在匹配图 M(G) 中，顶点的度数应为 1 或 0，其中边应从图 G 入射。

符号- M(G)

例子

匹配图 匹配规则

在一次搭配中，

如果 deg(V) = 1，则 (V) 被认为是匹配的

如果 deg(V) = 0，则 (V) 不匹配。

在匹配中，没有两条边是相邻的。这是因为如果任意两条边相邻，那么连接这两条边的顶点的度数将为 2，这违反了匹配规则。

最大匹配

如果“G”的其他边不能添加到 M 中，则图“G”的匹配 M 被称为最大。

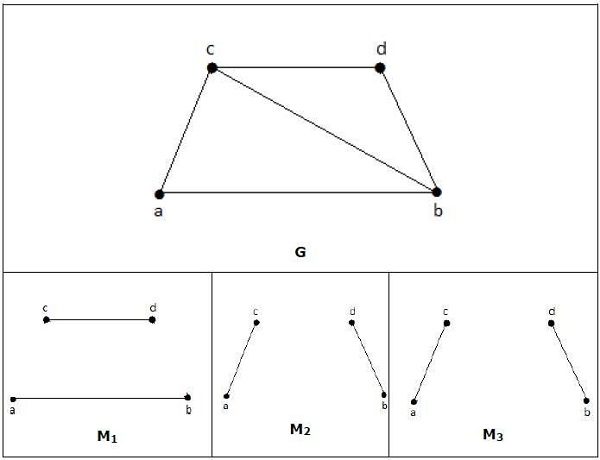
例子

G的最大匹配

上图中的M1、M2、M3是G的最大匹配。

最大匹配

它也称为最大最大匹配。最大匹配定义为具有最大边数的最大匹配。

'G'的最大匹配中的边数称为其匹配数。

例子

最大匹配

对于上面例子中给出的图，M1和M2是'G'的最大匹配，其匹配数为2。因此，通过使用图G，我们只能形成最多只有2条边的子图。因此我们得到的匹配数是两个。

完美搭配

如果图 g (G) 的每个顶点恰好与匹配 (M) 的一条边相关，则图 (G) 的匹配 (M) 被称为完美匹配，即

度(V) = 1 ∀ V

子图中每个顶点的度数都应该为 1。

例子

下图中，M1和M2是G完美匹配的例子。

完美搭配

注意- 图的每个完美匹配也是图的最大匹配，因为在完美匹配图中没有机会再添加一条边。

图的最大匹配不必是完美的。如果图“G”具有完美匹配，则顶点数 |V(G)| 甚至。如果是奇数，则最后一个顶点与另一个顶点配对，最后剩下一个顶点，该顶点不能与度数为零的任何其他顶点配对。显然违反了完美匹配原则。

例子

完美匹配图

注意- 上述陈述的反面不一定成立。如果 G 有偶数个顶点，则 M1 不必是完美的。

例子

顶点数

它是匹配的，但不是完美匹配，即使它有偶数个顶点。

图论 - 独立集

独立集合用集合来表示，其中

  • 不应有任何边缘彼此相邻。任何两条边之间不应有任何公共顶点。

  • 不应有任何顶点彼此相邻。任何两个顶点之间不应有任何公共边。

独立线组

让 'G' = (V, E) 成为一个图。如果 L 中没有两条边相邻，则 E 的子集 L 称为“G”的独立线集。这样的集合称为独立线集。

例子

独立线组

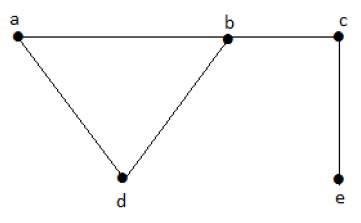
让我们考虑以下子集 -

L1 = {a,b}
L2 = {a,b} {c,e}
L3 = {a,d} {b,c}

在此示例中，子集 L2 和 L3 显然不是给定图中的相邻边。它们是独立的线路组。但L1并不是一个独立的线集，要制作一个独立的线集，至少要有两条边。

最大独立线集

如果“G”的其他边不能添加到“L”，则独立线集被称为图“G”的最大独立线集。

例子

最大独立线集

让我们考虑以下子集 -

L1 = {a, b}
L2 = {{b, e}, {c, f}}
L3 = {{a, e}, {b, c}, {d, f}}
L4 = {{a, b}, {c, f}}

L 2和L 3是最大独立线集/最大匹配。对于仅这两个子集，没有机会添加任何其他不相邻的边。因此这两个子集被认为是最大独立线集。

最大独立线集

具有最大边数的最大独立线集“G”称为最大独立线集“G”。

Number of edges in a maximum independent line set of G (β1)
   = Line independent number of G
   = Matching number of G

例子

最大独立线集

让我们考虑以下子集 -

L1 = {a, b}
L2 = {{b, e}, {c, f}}
L3 = {{a, e}, {b, c}, {d, f}}
L4 = {{a, b}, {c, f}}

L 3是 G 的最大独立线集，其最大边不是图中的相邻边，记为 β1 = 3。

注- 对于任何没有孤立顶点的图 G，

α1 + β1 = 图中的顶点数 = |V|

例子

行覆盖 K n /C n /w n的数量，

$$\alpha 1 = \lceil\frac{n}{2}\rceil\begin{cases}\frac{n}{2}\:如果\:n\:是偶数 \\\frac{n+ 1}{2}\:如果\:n\:是奇数\end{情况}$$

行无关数（匹配数）=β 1 = [n/2] α 1 + β 1 = n。

独立顶点集

让 'G' = (V, E) 成为一个图。如果“S”中没有两个顶点相邻，则“V”的子集称为“G”的独立集。

例子

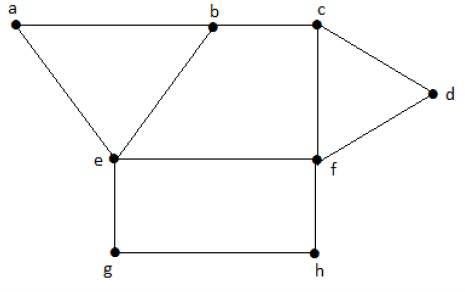
独立顶点集

考虑上图中的以下子集 -

S1 = {e}

S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}

显然S 1不是独立的顶点集，因为为了获得独立的顶点集，图中至少应该有两个顶点。但这里的情况并非如此。子集S 2、S 3和S 4是独立的顶点集，因为没有顶点与子集中的任何一个顶点相邻。

最大独立顶点集

假设“G”是一个图，那么如果“G”中没有其他顶点可以添加到“S”中，则“G”的独立顶点集被认为是最大的。

例子

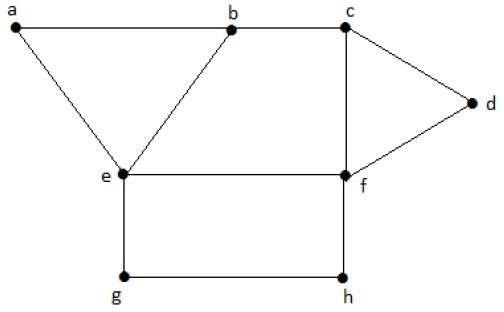
最大独立顶点集

考虑上图中的以下子集。

S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}

S 2和S 3是“G”的最大独立顶点集。在S 1和S 4中，我们可以添加其他顶点；但在 S 2和 S 3中，我们不能添加任何其他顶点。

最大独立顶点集

具有最大顶点数的“G”的最大独立顶点集称为最大独立顶点集。

例子

最大独立顶点集

考虑上图中的以下子集 -

S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}

只有 S 3是最大独立顶点集，因为它覆盖的顶点数量最多。'G'的最大独立顶点集合中的顶点数称为G的独立顶点数(β 2 )。

例子

对于完整图 K n，

顶点覆盖数 = α 2 = n−1

顶点独立数 = β 2 = 1

你有 α 2 + β 2 = n

在完全图中，每个顶点都与其剩余的 (n − 1) 个顶点相邻。因此，K n的最大独立集合仅包含一个顶点。

因此，β 2 =1

且α 2 =|v| − β 2 = n-1

注意- 对于任何图 'G' = (V, E)

  • α 2 + β 2 = |v|
  • 如果'S'是'G'的独立顶点集，则(V – S)是G的顶点覆盖。

图论 - 着色

图着色只不过是在某些约束下标记图组件（例如顶点、边和区域）的简单方法。在图中，没有两个相邻的顶点、相邻的边或相邻的区域是用最小数量的颜色着色的。这个数称为色数，该图称为正确着色图。

在图着色时，在图上设置的约束是颜色、着色顺序、分配颜色的方式等。着色被赋予给顶点或特定区域。因此，具有相同颜色的顶点或区域形成独立的集合。

顶点着色

顶点着色是将颜色分配给图“G”的顶点，使得没有两个相邻顶点具有相同的颜色。简单地说，一条边的两个顶点不应该具有相同的颜色。

色数

图“G”的顶点着色所需的最小颜色数称为G的色数，用X(G)表示。

当且仅当“G”是空图时，χ(G) = 1。如果“G”不是空图，则 χ(G) ≥ 2。

例子

顶点着色

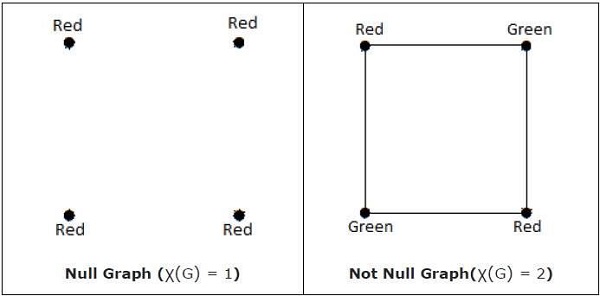
注- 如果存在最多使用 n 种颜色的顶点着色，即 X(G) ≤ n，则称图“G”是 n 可覆盖的。

区域着色

区域着色是对平面图区域的颜色分配，使得没有两个相邻区域具有相同的颜色。如果两个区域具有公共边缘，则称它们相邻。

例子

看一下下图。区域“aeb”和“befc”相邻，因为这两个区域之间有公共边“be”。

区域着色

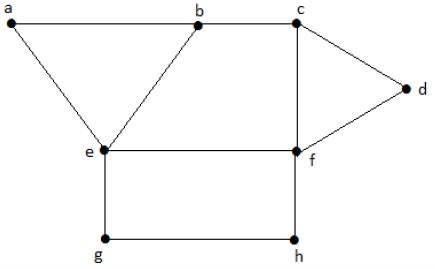
同样，其他区域也根据邻接程度进行着色。该图的颜色如下 -

基于颜色

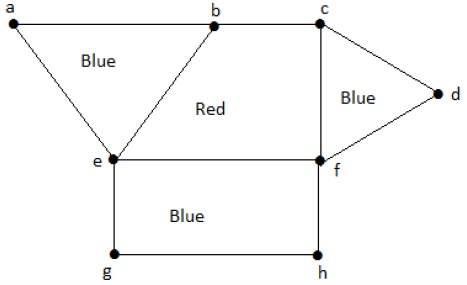
例子

Kn 的色数为

  • n
  • n–1
  • [n/2]
  • [n/2]

考虑这个例子 K 4。

顶点相邻

在完整图中，每个顶点都与剩余的 (n – 1) 个顶点相邻。因此，每个顶点都需要一种新颜色。因此色数 K n = n。

图形着色的应用

图着色是图论中最重要的概念之一。它用于计算机科学的许多实时应用，例如 -

  • 聚类
  • 数据挖掘
  • 图像捕捉
  • 图像分割
  • 联网
  • 资源分配
  • 进程调度

图论-同构

图可以以具有相同数量的顶点、边以及相同的边连通性的不同形式存在。这样的图称为同构图。请注意，我们在本章中对图表进行标记主要是为了引用它们并相互识别它们。

同构图

两个图 G 1和 G 2被称为同构如果 -

  • 它们的组件数量（顶点和边）相同。

  • 它们的边缘连接性被保留。

注意- 简而言之，在两个同构图中，一个是另一个的调整版本。未标记的图也可以被视为同构图。

There exists a function ‘f’ from vertices of G1 to vertices of G2
   [f: V(G1) ⇒ V(G2)], such that
Case (i): f is a bijection (both one-one and onto)
Case (ii): f preserves adjacency of vertices, i.e., if the edge {U, V} ∈ G1, then the
edge {f(U), f(V)} ∈ G2, then G1 ≡ G2.

笔记

如果 G 1 ≠ G 2则 -

|V(G 1 )| = |V(G 2 )|

|E(G 1 )| = |E(G 2 )|

度