图论 - 着色

图着色只不过是在某些约束下标记图组件（例如顶点、边和区域）的简单方法。在图中，没有两个相邻的顶点、相邻的边或相邻的区域是用最小数量的颜色着色的。这个数称为色数，该图称为正确着色图。

在图着色时，在图上设置的约束是颜色、着色顺序、分配颜色的方式等。着色被赋予给顶点或特定区域。因此，具有相同颜色的顶点或区域形成独立的集合。

顶点着色

顶点着色是将颜色分配给图“G”的顶点，使得没有两个相邻顶点具有相同的颜色。简单地说，一条边的两个顶点不应该具有相同的颜色。

图“G”的顶点着色所需的最小颜色数称为G的色数，用X(G)表示。

当且仅当“G”是空图时，χ(G) = 1。如果“G”不是空图，则 χ(G) ≥ 2。

例子

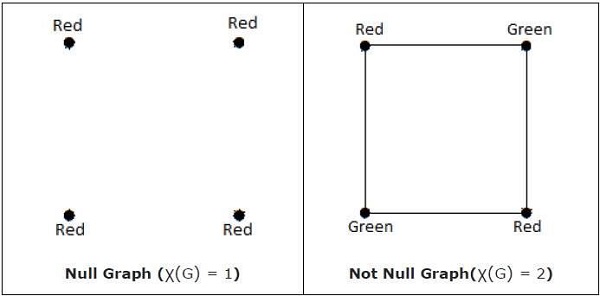
注- 如果存在最多使用 n 种颜色的顶点着色，即 X(G) ≤ n，则称图“G”是 n 可覆盖的。

区域着色是对平面图区域的颜色分配，使得没有两个相邻区域具有相同的颜色。如果两个区域具有公共边缘，则称它们相邻。

例子

看一下下图。区域“aeb”和“befc”相邻，因为这两个区域之间有公共边“be”。

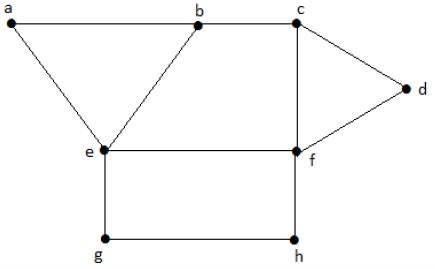
同样，其他区域也根据邻接程度进行着色。该图的颜色如下 -

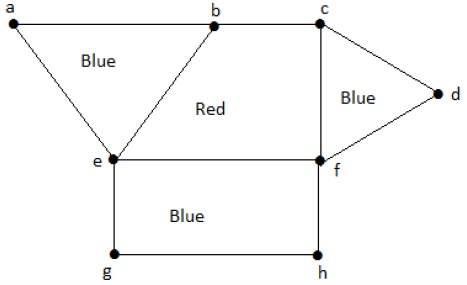
例子

Kn 的色数为

考虑这个例子 K ₄。

在完整图中，每个顶点都与剩余的 (n – 1) 个顶点相邻。因此，每个顶点都需要一种新颜色。因此色数 K _n = n。

图着色是图论中最重要的概念之一。它用于计算机科学的许多实时应用，例如 -