机器学习 - 技能

---

机器学习的宽度非常大，需要跨多个领域的技能。下面列出了成为机器学习专家所需掌握的技能 -

• 统计数据
• 概率论
• 结石
• 优化技术
• 可视化

机器学习各种技能的必要性

为了让您简要了解需要获得哪些技能，让我们讨论一些例子 -

数学符号

大多数机器学习算法都很大程度上基于数学。您需要了解的数学水平可能只是初级水平。重要的是您应该能够阅读数学家在方程中使用的符号。例如，如果您能够阅读符号并理解其含义，那么您就已经准备好学习机器学习了。如果没有，您可能需要温习数学知识。

$$f_{AN}(net-\theta)=\begin{cases}\gamma & if\:net-\theta \geq \epsilon\\net-\theta & if - \epsilon< net-\theta <\ epsilon\\ -\gamma & if\:net-\theta\leq- \epsilon\end{情况}$$

$$\displaystyle\\\max\limits_{\alpha}\begin{bmatrix}\displaystyle\sum\limits_{i=1}^m \alpha-\frac{1}{2}\displaystyle\sum\limits_{ i,j=1}^m 标签^\left(\begin{array}{c}i\\ \end{array}\right)\cdot\:label^\left(\begin{array}{c}j \\ \end{array}\right)\cdot\:a_{i}\cdot\:a_{j}\langle x^\left(\begin{array}{c}i\\ \end{array}\右),x^\left(\begin{array}{c}j\\ \end{array}\right)\rangle \end{bmatrix}$$

$$f_{AN}(net-\theta)=\left(\frac{e^{\lambda(net-\theta)}-e^{-\lambda(net-\theta)}}{e^{ \lambda(net-\theta)}+e^{-\lambda(net-\theta)}}\right)\;$$

概率论

这是一个测试您当前概率论知识的示例：用条件概率进行分类。

$$p(c_{i}|x,y)\;=\frac{p(x,y|c_{i})\;p(c_{i})\;}{p(x,y)\ ;}$$

通过这些定义，我们可以定义贝叶斯分类规则 -

• 如果 P(c1|x, y) > P(c2|x, y) ，则类别为 c1 。
• 如果 P(c1|x, y) < P(c2|x, y) ，则类别为 c2 。

最优化问题

这是一个优化函数

$$\displaystyle\\\max\limits_{\alpha}\begin{bmatrix}\displaystyle\sum\limits_{i=1}^m \alpha-\frac{1}{2}\displaystyle\sum\limits_{ i,j=1}^m 标签^\left(\begin{array}{c}i\\ \end{array}\right)\cdot\:label^\left(\begin{array}{c}j \\ \end{array}\right)\cdot\:a_{i}\cdot\:a_{j}\langle x^\left(\begin{array}{c}i\\ \end{array}\右),x^\left(\begin{array}{c}j\\ \end{array}\right)\rangle \end{bmatrix}$$

受以下限制 -

$$\alpha\geq0,and\:\displaystyle\sum\limits_{i-1}^m \alpha_{i}\cdot\:label^\left(\begin{array}{c}i\\ \end {数组}\右)=0$$

如果您能够阅读并理解以上内容，那么您就已经准备好了。

可视化

在许多情况下，您需要了解各种类型的可视化图，以了解数据分布并解释算法输出的结果。

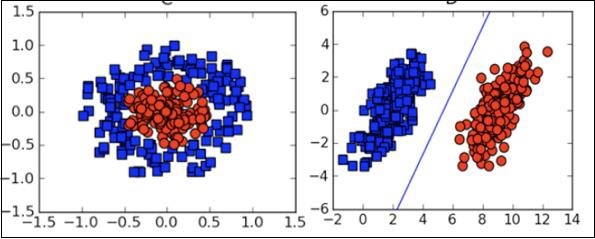
除了上述机器学习的理论方面之外，您还需要良好的编程技能来编写这些算法。

那么实施机器学习需要什么？让我们在下一章中探讨这一点。