晶体振荡器
当振荡器连续工作时,其频率稳定性就会受到影响。其频率发生变化。影响振荡器频率的主要因素是
- 电源变化
- 温度变化
- 负载或输出电阻的变化
在 RC 和 LC 振荡器中,电阻、电容和电感的值随温度变化,因此频率会受到影响。为了避免这个问题,压电晶体被用于振荡器。
在并联谐振电路中使用压电晶体可以提高振荡器的频率稳定性。这种振荡器称为晶体振荡器。
晶体振荡器
晶体振荡器的原理取决于压电效应。晶体的自然形状是六角形。当晶体片垂直于X轴切割时,称为X切割;当沿Y轴切割时,称为Y切割。
晶体振荡器中使用的晶体表现出一种称为压电特性的特性。那么,让我们对压电效应有一个了解。
压电效应
该晶体具有这样的特性:当在晶体的一个面上施加机械应力时,在晶体的相对面上会产生电势差。相反,当在其中一个面上施加电势差时,会沿着其他面产生机械应力。这称为压电效应。
某些晶体材料如罗谢尔盐、石英和电气石等表现出压电效应,此类材料被称为压电晶体。石英是最常用的压电晶体,因为它价格便宜并且在自然界中容易获得。
当压电晶体受到适当的交变电势时,它会发生机械振动。当交流电压的频率等于晶体的固有频率时,机械振动的幅度达到最大。
石英晶体的工作原理
为了使晶体在电子电路中工作,晶体以电容器的形式放置在两个金属板之间。石英是最常用的晶体类型,因为它的可用性和坚固性同时价格低廉。交流电压并联施加到晶体上。
石英晶体的电路布置如下所示 -
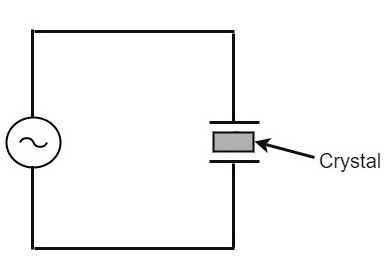
如果施加交流电压,晶体开始以所施加电压的频率振动。然而,如果施加电压的频率等于晶体的固有频率,则发生共振并且晶体振动达到最大值。该固有频率几乎是恒定的。
晶体的等效电路
如果我们试图用等效电路来表示晶体,我们必须考虑两种情况,即晶体何时振动和不振动。下图分别表示晶体的符号和等效电路。
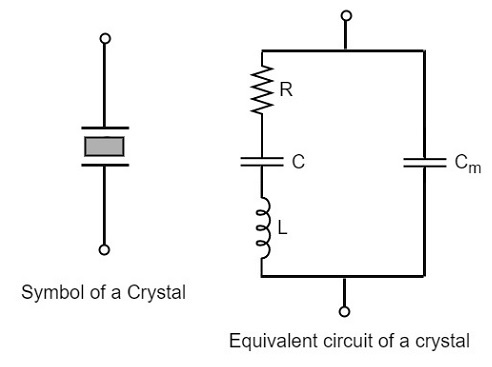
上述等效电路由串联RLC电路与电容C m并联组成。当安装在交流电源两端的晶体不振动时,它相当于电容 C m。当晶体振动时,它的作用就像一个调谐的 RLC 电路。
频率响应
晶体的频率响应如下所示。该图显示了电抗(XL或X C)与频率 (f) 的关系。很明显,晶体具有两个间隔很近的谐振频率。
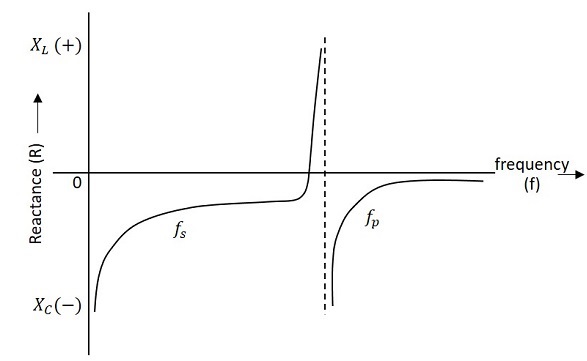
第一个是串联谐振频率 (f s ),当电感 (L) 的电抗等于电容 C 的电抗时,就会出现串联谐振频率。在这种情况下,等效电路的阻抗等于电阻 R,并且振荡频率由以下关系给出,
$$f = \frac{1}{2\pi \sqrt{LC}}$$
第二个是并联谐振频率(f p),当 RLC 支路的电抗等于电容器 C m的电抗时发生。在此频率下,晶体向外部电路提供非常高的阻抗,振荡频率由以下关系式给出。
$$f_p = \frac{1}{2\pi \sqrt{L.C_T}}$$
在哪里
$$C_T = \frac{C C_m}{(C + C_m)}$$
与C相比, C m的值通常非常大。因此,C T的值近似等于C,并且因此串联谐振频率近似等于并联谐振频率(即,f s = f p)。
晶体振荡器电路
晶体振荡器电路可以通过多种方式构建,例如晶体控制调谐集电极振荡器、Colpitts晶体振荡器、Clap晶体振荡器等。但晶体管皮尔斯晶体振荡器是最常用的一种。这是通常称为晶体振荡器电路的电路。
下面的电路图显示了晶体管皮尔斯晶体振荡器的布置。
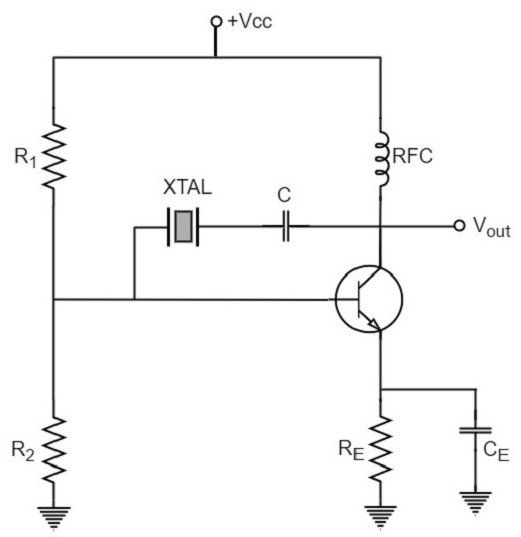
在此电路中,晶体作为串联元件连接在从集电极到基极的反馈路径中。电阻器R 1、R 2和R E提供分压器稳定的直流偏置电路。电容器C E提供发射极电阻器的交流旁路,RFC(射频扼流圈)线圈提供直流偏置,同时将电源线上的任何交流信号去耦,以免影响输出信号。耦合电容C在电路工作频率下的阻抗可以忽略不计。但它会阻止集电极和基极之间的任何直流电。
电路振荡频率由晶体的串联谐振频率决定,其值由下式给出:
$$f_o = \frac{1}{2\pi \sqrt{LC}}$$
值得注意的是,电源电压、晶体管器件参数等的变化对电路工作频率没有影响,电路工作频率由晶体保持稳定。
优点
晶体振荡器的优点如下 -
- 它们具有很高的频率稳定性。
- 晶体的品质因数 (Q) 非常高。
缺点
晶体振荡器的缺点如下 -
- 它们很脆弱,可用于低功率电路。
- 振荡频率不能明显改变。
振荡器的频率稳定性
振荡器需要在较长时间内保持其频率而不发生任何变化,以便为电路操作提供更平滑、清晰的正弦波输出。因此,对于振荡器(无论是正弦还是非正弦)而言,频率稳定性这一术语确实非常重要。
振荡器的频率稳定性定义为振荡器在尽可能长的时间间隔内保持所需频率恒定的能力。让我们尝试讨论影响频率稳定性的因素。
工作点变化
我们已经了解了晶体管参数并了解了工作点的重要性。对于放大电路中使用的晶体管(BJT 或 FET),该工作点的稳定性需要更高的考虑。
所使用的有源器件的操作被调整到其特性的线性部分。该点由于温度变化而移动,因此稳定性受到影响。
温度变化
振荡电路中的储能电路包含各种频率确定元件,例如电阻器、电容器和电感器。它们的所有参数都与温度相关。由于温度的变化,它们的值会受到影响。这带来了振荡电路频率的变化。
由于电源
供电功率的变化也会影响频率。电源的变化导致V cc的变化。这将影响产生的振荡的频率。
为了避免这种情况,采用了稳压电源系统。这简称为 RPS。稳压电源的细节已在电子电路教程的电源部分进行了清楚的讨论。
输出负载变化
输出电阻或输出负载的变化也会影响振荡器的频率。当连接负载时,储能电路的有效电阻发生变化。结果,LC调谐电路的Q因数发生改变。这导致振荡器的输出频率发生变化。
元件间电容的变化
元件间电容是在二极管和晶体管等 PN 结材料中产生的电容。这些是由于它们在运行过程中存在电荷而产生的。
由于温度、电压等各种原因,元件间电容器会发生变化。这个问题可以通过在有问题的元件间电容器上连接沼泽电容器来解决。
Q值
振荡器中的 Q(品质因数)值必须很高。调谐振荡器中的 Q 值决定了选择性。由于该 Q 值与调谐电路的频率稳定性成正比,因此 Q 值应保持较高。
频率稳定性可以在数学上表示为:
$$S_w = d\theta/dw$$
其中 dθ 是标称频率 f r发生微小频率变化时引入的相移。(dθ/dw)值越大,电路的振荡频率越稳定。
