振荡器电路
振荡器电路是有助于产生振荡的电路所有部分的完整集合。正如之前所讨论的,这些振荡应该持续并且应该不受阻尼。让我们尝试分析一个实际的振荡器电路,以更好地了解振荡器电路的工作原理。
实用振荡器电路
实用的振荡器电路由储能电路、晶体管放大器和反馈电路组成。下面的电路图显示了实际振荡器的布置。
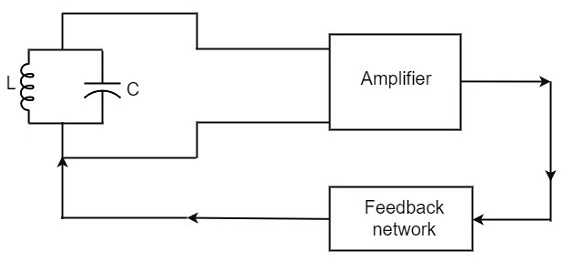
现在让我们讨论这个实用振荡器电路的各个部分。
储能电路- 储能电路由与电容器C并联的电感 L 组成。这两个元件的值决定了振荡电路的频率,因此称为频率确定电路。
晶体管放大器- 储能电路的输出连接到放大器电路,以便放大储能电路产生的振荡。因此,放大器增加了这些振荡的输出。
反馈电路- 反馈电路的功能是将部分输出能量以适当的相位传输到LC电路。该反馈在振荡器中为正反馈,而在放大器中为负反馈。
振荡器的频率稳定性
振荡器的频率稳定性是衡量其在较长时间间隔内保持恒定频率的能力的指标。当工作时间较长时,振荡器频率可能会因增加或减少而偏离先前设定的值。
振荡器频率的变化可能是由于以下因素引起的 -
使用的有源器件(例如 BJT 或 FET)的工作点应位于放大器的线性区域内。它的偏差会影响振荡器的频率。
电路元件性能的温度依赖性会影响振荡器频率。
施加到有源器件的直流电源电压的变化会改变振荡器频率。如果使用稳压电源,则可以避免这种情况。
输出负载的变化可能会导致储能电路的 Q 因数发生变化,从而导致振荡器输出频率发生变化。
元件间电容和杂散电容的存在会影响振荡器的输出频率,从而影响频率稳定性。
巴克豪森准则
根据目前所掌握的知识,我们了解到实际的振荡器电路由储能电路、晶体管放大器电路和反馈电路组成。因此,现在让我们尝试温习反馈放大器的概念,以导出反馈放大器的增益。
反馈放大器原理
反馈放大器通常由两部分组成。它们是放大器和反馈电路。反馈电路通常由电阻组成。反馈放大器的概念可以通过下图来理解。
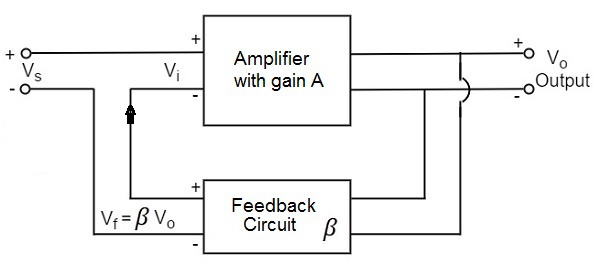
由上图可知,放大器的增益用A表示。放大器的增益是输出电压Vo与输入电压V i的比值。反馈网络从放大器的输出V o中提取电压V f = β V o 。
对于正反馈,从信号电压V s中添加该电压,对于负反馈,从信号电压V s 中减去该电压。
因此,为了获得积极的反馈,
Vi = V s + V f = V s + β V o
β = V f /V o的量称为反馈比或反馈分数。
输出V o必须等于输入电压(V s + βV o ) 乘以放大器的增益A。
因此,
$$(V_s + \beta V_o)A = V_o$$
或者
$$AV_s + A\beta V_o = V_o$$
或者
$$AV_s = V_o(1 - A\beta)$$
所以
$$\frac{V_o}{V_s} = \frac{A}{1 - A\beta}$$
令 A f为放大器的总增益(带反馈的增益)。这被定义为输出电压 V o与施加的信号电压 V s的比率,即
$$A_f = \frac{输出\:电压}{输入\:信号\:电压} = \frac{V_o}{V_s}$$
从上面两个方程我们可以看出,正反馈反馈放大器的增益方程为
$$A_f = \frac{A}{1 - A\beta}$$
其中Aβ是反馈因子或环路增益。
如果 Aβ = 1,则 A f = ∞。这样增益就变成无穷大,即没有任何输入就有输出。换句话说,放大器充当振荡器。
条件 Aβ = 1 称为巴克豪森振荡准则。在振荡器的概念中,这是一个需要始终牢记的非常重要的因素。
