正弦振荡器 - 基本概念
具有正反馈的放大器产生与输入同相的输出,并增加信号的强度。正反馈也称为退化反馈或直接反馈。这种反馈构成了反馈放大器,即振荡器。
正反馈的使用导致反馈放大器的闭环增益大于开环增益。它会导致不稳定并作为振荡电路运行。振荡电路提供任何所需频率的不断变化的放大输出信号。
振荡电路
振荡电路产生所需频率的电振荡。它们也称为储能电路。
简单的储能电路由电感器 L 和电容器 C 组成,两者共同决定电路的振荡频率。
为了理解振荡电路的概念,让我们考虑以下电路。该电路中的电容器已使用直流电源充电。在这种情况下,电容器的上极板电子过剩,而下极板电子不足。电容器保留一些静电能量,并且电容器两端有电压。
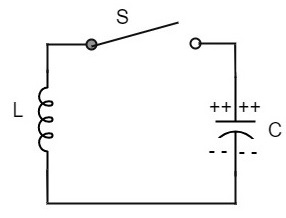
当开关S闭合时,电容器放电,电流流过电感。由于感应效应,电流缓慢增加至最大值。一旦电容器完全放电,线圈周围的磁场就达到最大。
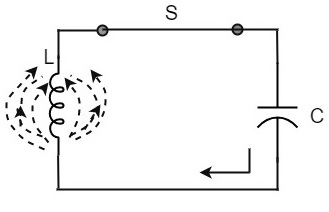
现在,让我们进入下一阶段。一旦电容器完全放电,磁场就会开始崩溃,并根据楞次定律产生反电动势。现在,电容器上极板带正电荷,下极板带负电荷。
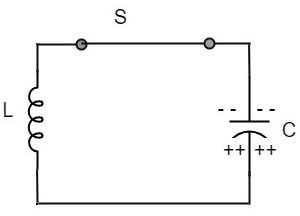
一旦电容器充满电,它就会开始放电,在线圈周围形成磁场,如下电路图所示。
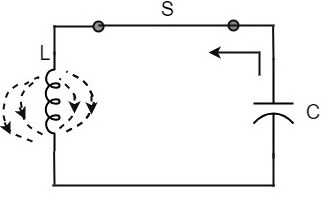
这种充电和放电的持续导致电子的交替运动或振荡电流。L和C之间的能量交换产生连续振荡。
在没有损耗的理想电路中,振荡将无限期地持续下去。在实际的储能电路中,会产生诸如线圈中的电阻损耗和辐射损耗以及电容器中的介电损耗等损耗。这些损耗导致阻尼振荡。
振荡频率
储能电路产生的振荡频率由储能电路的组件L和C决定。振荡的实际频率是储能电路的谐振频率(或固有频率),由下式给出
$$f_r = \frac{1}{2 \pi \sqrt{LC}}$$
电容器的容量
振荡频率fo与电容器电容的平方根成反比。因此,如果所使用的电容器的值较大,则充电和放电时间也会较长。因此频率会较低。
从数学上来说,频率,
$$f_o \propto 1\sqrt{C}$$
线圈的自感
振荡频率fo与线圈自感的平方根成正比。如果电感值较大,则对电流变化的阻力较大,因此完成每个周期所需的时间会较长,这意味着时间周期较长,频率较低。
从数学上来说,频率,
$$f_o \propto 1\sqrt{L}$$
结合以上两个方程,
$$f_o \propto \frac{1}{\sqrt{LC}}$$
$$f_o = \frac{1}{2 \pi \sqrt{LC}}$$
上式虽然表示输出频率,但与储能电路的固有频率或谐振频率相匹配。
