CNTK - 循环神经网络

现在，让我们了解如何在 CNTK 中构建循环神经网络（RNN）。

介绍

我们学习了如何使用神经网络对图像进行分类，这是深度学习中的标志性工作之一。但是，神经网络擅长且正在进行大量研究的另一个领域是循环神经网络（RNN）。在这里，我们将了解什么是 RNN 以及如何在需要处理时间序列数据的场景中使用它。

什么是循环神经网络？

循环神经网络（RNN）可以被定义为能够随时间进行推理的特殊类型的神经网络。RNN主要用于需要处理随时间变化的值的场景，即时间序列数据。为了更好地理解它，让我们对常规神经网络和循环神经网络进行一个小小的比较 -

  • 众所周知，在常规神经网络中，我们只能提供一个输入。这限制了它只能产生一个预测。举个例子，我们可以使用常规神经网络来完成文本翻译工作。

  • 另一方面，在循环神经网络中，我们可以提供导致单个预测的样本序列。换句话说，使用 RNN，我们可以根据输入序列预测输出序列。例如，RNN 在翻译任务中已经有不少成功的实验。

循环神经网络的用途

RNN 可以通过多种方式使用。其中一些如下 -

预测单个输出

在深入研究 RNN 如何基于序列预测单个输出的步骤之前，让我们看看基本的 RNN 是什么样子的：

单路输出

正如我们在上图中所看到的，RNN 包含一个到输入的环回连接，每当我们输入一个值序列时，它都会以时间步长的方式处理序列中的每个元素。

此外，由于环回连接，RNN 可以将生成的输出与序列中下一个元素的输入相结合。通过这种方式，RNN 将在整个序列上建立一个记忆，可用于进行预测。

为了使用 RNN 进行预测，我们可以执行以下步骤 -

  • 首先，为了创建初始隐藏状态，我们需要输入输入序列的第一个元素。

  • 之后，为了生成更新的隐藏状态，我们需要获取初始隐藏状态并将其与输入序列中的第二个元素组合。

  • 最后，为了生成最终的隐藏状态并预测 RNN 的输出，我们需要获取输入序列中的最终元素。

通过这种方式，借助环回连接，我们可以教 RNN 识别随时间推移发生的模式。

预测序列

上面讨论的 RNN 基本模型也可以扩展到其他用例。例如，我们可以使用它来根据单个输入预测一系列值。在这种情况下，为了使用 RNN 进行预测，我们可以执行以下步骤 -

  • 首先，为了创建初始隐藏状态并预测输出序列中的第一个元素，我们需要将输入样本输入神经网络。

  • 之后，为了生成更新的隐藏状态和输出序列中的第二个元素，我们需要将初始隐藏状态与相同的样本组合起来。

  • 最后，为了再次更新隐藏状态并预测输出序列中的最终元素，我们再次输入样本。

预测序列

正如我们已经看到的如何基于序列预测单个值以及如何基于单个值预测序列。现在让我们看看如何预测序列的序列。在这种情况下，为了使用 RNN 进行预测，我们可以执行以下步骤 -

  • 首先，为了创建初始隐藏状态并预测输出序列中的第一个元素，我们需要获取输入序列中的第一个元素。

  • 之后，为了更新隐藏状态并预测输出序列中的第二个元素，我们需要采用初始隐藏状态。

  • 最后，为了预测输出序列中的最终元素，我们需要获取更新的隐藏状态和输入序列中的最终元素。

RNN 的工作原理

要了解循环神经网络 (RNN) 的工作原理，我们需要首先了解网络中的循环层如何工作。首先让我们讨论 e 如何使用标准循环层预测输出。

使用标准 RNN 层预测输出

正如我们之前讨论的，RNN 中的基本层与神经网络中的常规层有很大不同。在上一节中，我们还在图中演示了 RNN 的基本架构。为了更新第一次步入序列的隐藏状态，我们可以使用以下公式 -

循环层

在上面的等式中，我们通过计算初始隐藏状态和一组权重之间的点积来计算新的隐藏状态。

现在，对于下一步，当前时间步的隐藏状态用作序列中下一个时间步的初始隐藏状态。这就是为什么，要更新第二个时间步的隐藏状态，我们可以重复第一个时间步中执行的计算，如下所示 -

第一步

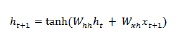
接下来，我们可以重复更新序列中第三步也是最后一步隐藏状态的过程，如下所示 -

最后一步

当我们按顺序处理完上述所有步骤后，我们可以计算输出如下 -

计算输出

对于上面的公式，我们使用了第三组权重和最终时间步的隐藏状态。

高级循环单元

基本循环层的主要问题是梯度消失问题，因此它不太擅长学习长期相关性。简而言之，基本循环层不能很好地处理长序列。这就是其他一些更适合处理较长序列的循环层类型的原因，如下所示 -

长短期记忆 (LSTM)

长短期记忆 (LSTM)

长短期记忆 (LSTM) 网络由 Hochreiter 和 Schmidhuber 提出。它解决了让基本循环层长期记住事物的问题。LSTM 的架构如上图所示。正如我们所看到的，它有输入神经元、记忆细胞和输出神经元。为了解决梯度消失问题，长期短期记忆网络使用显式记忆单元（存储先前的值）和以下门 -

  • 忘记门- 顾名思义，它告诉存储单元忘记以前的值。存储单元存储这些值，直到门（即“忘记门”）告诉它忘记它们。

  • 输入门- 顾名思义，它向单元添加新的东西。

  • 输出门- 顾名思义，输出门决定何时将向量从单元传递到下一个隐藏状态。

门控循环单元 (GRU)

门控循环单元 (GRU)

梯度循环单元(GRU) 是 LSTM 网络的轻微变体。它少了一个门，并且接线方式与 LSTM 略有不同。其架构如上图所示。它具有输入神经元、门控记忆细胞和输出神经元。门控循环单元网络有以下两个门 -

  • 更新门- 它决定以下两件事 -

    • 应保留最后状态的多少信息？

    • 应该从前一层输入多少信息？

  • 重置门- 重置门的功能与 LSTM 网络的遗忘门非常相似。唯一的区别是它的位置略有不同。

与长短期记忆网络相比，门控循环单元网络速度稍快且更容易运行。

创建RNN结构

在开始对任何数据源的输出进行预测之前，我们需要首先构建 RNN，构建 RNN 与我们在上一节中构建常规神经网络完全相同。以下是构建代码 -

from cntk.losses import squared_error
from cntk.io import CTFDeserializer, MinibatchSource, INFINITELY_REPEAT, StreamDefs, StreamDef
from cntk.learners import adam
from cntk.logging import ProgressPrinter
from cntk.train import TestConfig
BATCH_SIZE = 14 * 10
EPOCH_SIZE = 12434
EPOCHS = 10

多层放样

我们还可以在 CNTK 中堆叠多个循环层。例如，我们可以使用以下层组合 -

from cntk import sequence, default_options, input_variable
from cntk.layers import Recurrence, LSTM, Dropout, Dense, Sequential, Fold
features = sequence.input_variable(1)
with default_options(initial_state = 0.1):
   model = Sequential([
      Fold(LSTM(15)),
      Dense(1)
   ])(features)
target = input_variable(1, dynamic_axes=model.dynamic_axes)

正如我们在上面的代码中看到的，我们有以下两种方法可以在 CNTK 中对 RNN 进行建模 -

  • 首先，如果我们只想要循环层的最终输出，我们可以将Fold层与循环层结合使用，例如 GRU、LSTM，甚至 RNNStep。

  • 其次，作为替代方法，我们还可以使用Recurrence块。

使用时间序列数据训练 RNN

一旦我们构建了模型，让我们看看如何在 CNTK 中训练 RNN -

from cntk import Function
@Function
def criterion_factory(z, t):
   loss = squared_error(z, t)
   metric = squared_error(z, t)
   return loss, metric
loss = criterion_factory(model, target)
learner = adam(model.parameters, lr=0.005, momentum=0.9)

现在要将数据加载到训练过程中，我们必须从一组 CTF 文件中反序列化序列。以下代码具有create_datasource函数，这是创建训练和测试数据源的有用实用函数。

target_stream = StreamDef(field='target', shape=1, is_sparse=False)
features_stream = StreamDef(field='features', shape=1, is_sparse=False)
deserializer = CTFDeserializer(filename, StreamDefs(features=features_stream, target=target_stream))
   datasource = MinibatchSource(deserializer, randomize=True, max_sweeps=sweeps)
return datasource
train_datasource = create_datasource('Training data filename.ctf')#we need to provide the location of training file we created from our dataset.
test_datasource = create_datasource('Test filename.ctf', sweeps=1) #we need to provide the location of testing file we created from our dataset.

现在，我们已经设置了数据源、模型和损失函数，我们可以开始训练过程了。它与我们在前面的基本神经网络部分中所做的非常相似。

progress_writer = ProgressPrinter(0)
test_config = TestConfig(test_datasource)
input_map = {
   features: train_datasource.streams.features,
   target: train_datasource.streams.target
}
history = loss.train(
   train_datasource,
   epoch_size=EPOCH_SIZE,
   parameter_learners=[learner],
   model_inputs_to_streams=input_map,
   callbacks=[progress_writer, test_config],
   minibatch_size=BATCH_SIZE,
   max_epochs=EPOCHS
)

我们将得到类似如下的输出 -

输出−

average  since  average  since  examples
loss      last  metric  last
------------------------------------------------------
Learning rate per minibatch: 0.005
0.4      0.4    0.4      0.4      19
0.4      0.4    0.4      0.4      59
0.452    0.495  0.452    0.495   129
[…]

验证模型

实际上，使用 RNN 进行预测与使用任何其他 CNK 模型进行预测非常相似。唯一的区别是，我们需要提供序列而不是单个样本。

现在，随着我们的 RNN 最终完成训练，我们可以通过使用一些样本序列来测试模型来验证模型，如下所示 -

import pickle
with open('test_samples.pkl', 'rb') as test_file:
test_samples = pickle.load(test_file)
model(test_samples) * NORMALIZE

输出−

array([[ 8081.7905],
[16597.693 ],
[13335.17 ],
...,
[11275.804 ],
[15621.697 ],
[16875.555 ]], dtype=float32)