CNTK - 回归模型

在这里，我们将研究如何衡量回归模型的性能。

验证回归模型的基础知识

我们知道，回归模型与分类模型不同，从某种意义上说，个体样本不存在正确或错误的二元衡量标准。在回归模型中，我们想要衡量预测与实际值的接近程度。预测值越接近预期输出，模型的性能就越好。

在这里，我们将使用不同的错误率函数来测量用于回归的神经网络的性能。

计算误差范围

如前所述，在验证回归模型时，我们无法判断预测是正确还是错误。我们希望我们的预测尽可能接近真实值。但是，这里的小误差范围是可以接受的。

误差范围的计算公式如下 -

误差范围

这里，

预测值=用帽子表示的y

实际值= y 预测值

首先，我们需要计算预测值和真实值之间的距离。然后，为了获得总体错误率，我们需要将这些平方距离相加并计算平均值。这称为均方误差函数。

但是，如果我们想要表示误差范围的性能数据，我们需要一个表示绝对误差的公式。平均绝对误差函数的公式如下 -

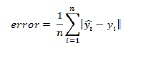
平均绝对值

上式取预测值与真实值之间的绝对距离。

使用 CNTK 测量回归性能

在这里，我们将看看如何使用我们与 CNTK 结合讨论的不同指标。我们将使用一个回归模型，使用下面给出的步骤来预测汽车每加仑的英里数。

实施步骤−

步骤 1 - 首先，我们需要从cntk包中导入所需的组件，如下所示 -

from cntk import default_option, input_variable
from cntk.layers import Dense, Sequential
from cntk.ops import relu

步骤 2 - 接下来，我们需要使用default_options函数定义默认激活函数。然后，创建一个新的 Sequential 层集并提供两个 Dense 层，每个层有 64 个神经元。然后，我们向顺序层集添加一个额外的密集层（将充当输出层），并给出 1 个没有激活的神经元，如下所示 -

with default_options(activation=relu):
model = Sequential([Dense(64),Dense(64),Dense(1,activation=None)])

步骤 3 - 创建网络后，我们需要创建一个输入特征。我们需要确保它与我们将用于训练的特征具有相同的形状。

features = input_variable(X.shape[1])

步骤 4 - 现在，我们需要创建另一个大小为 1 的input_variable。它将用于存储 NN 的期望值。

target = input_variable(1)
z = model(features)

现在，我们需要训练模型，为此，我们将分割数据集并使用以下实现步骤执行预处理 -

步骤 5 - 首先，从 sklearn.preprocessing 导入 StandardScaler 以获得 -1 和 +1 之间的值。这将帮助我们应对神经网络中的梯度爆炸问题。

from sklearn.preprocessing import StandardScalar

步骤 6 - 接下来，从 sklearn.model_selection 导入 train_test_split，如下所示 -

from sklearn.model_selection import train_test_split

步骤 7 -使用drop方法从数据集中删除mpg列。最后使用train_test_split函数将数据集分成训练集和验证集，如下所示 -

x = df_cars.drop(columns=[‘mpg’]).values.astype(np.float32)
y=df_cars.iloc[: , 0].values.reshape(-1, 1).astype(np.float32)
scaler = StandardScaler()
X = scaler.fit_transform(x)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

步骤 8 - 现在，我们需要创建另一个大小为 1 的 input_variable。它将用于存储 NN 的期望值。

target = input_variable(1)
z = model(features)

我们已经分割并预处理了数据，现在我们需要训练神经网络。正如前面几节创建回归模型时所做的那样，我们需要定义损失函数和度量函数的组合来训练模型。

import cntk
def absolute_error(output, target):
   return cntk.ops.reduce_mean(cntk.ops.abs(output – target))
@ cntk.Function
def criterion_factory(output, target):
   loss = squared_error(output, target)
   metric = absolute_error(output, target)
   return loss, metric

现在，让我们看看如何使用训练好的模型。对于我们的模型，我们将使用 criteria_factory 作为损失和度量组合。

from cntk.losses import squared_error
from cntk.learners import sgd
from cntk.logging import ProgressPrinter
progress_printer = ProgressPrinter(0)
loss = criterion_factory (z, target)
learner = sgd(z.parameters, 0.001)
training_summary=loss.train((x_train,y_train),parameter_learners=[learner],callbacks=[progress_printer],minibatch_size=16,max_epochs=10)

完整的实现示例

from cntk import default_option, input_variable
from cntk.layers import Dense, Sequential
from cntk.ops import relu
with default_options(activation=relu):
model = Sequential([Dense(64),Dense(64),Dense(1,activation=None)])
features = input_variable(X.shape[1])
target = input_variable(1)
z = model(features)
from sklearn.preprocessing import StandardScalar
from sklearn.model_selection import train_test_split
x = df_cars.drop(columns=[‘mpg’]).values.astype(np.float32)
y=df_cars.iloc[: , 0].values.reshape(-1, 1).astype(np.float32)
scaler = StandardScaler()
X = scaler.fit_transform(x)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
target = input_variable(1)
z = model(features)
import cntk
def absolute_error(output, target):
   return cntk.ops.reduce_mean(cntk.ops.abs(output – target))
@ cntk.Function
def criterion_factory(output, target):
loss = squared_error(output, target)
metric = absolute_error(output, target)
return loss, metric
from cntk.losses import squared_error
from cntk.learners import sgd
from cntk.logging import ProgressPrinter
progress_printer = ProgressPrinter(0)
loss = criterion_factory (z, target)
learner = sgd(z.parameters, 0.001)
training_summary=loss.train((x_train,y_train),parameter_learners=[learner],callbacks=[progress_printer],minibatch_size=16,max_epochs=10)

输出

-------------------------------------------------------------------
average  since   average   since  examples
loss     last    metric    last
------------------------------------------------------
Learning rate per minibatch: 0.001
690       690     24.9     24.9       16
654       636     24.1     23.7       48
[………]

为了验证我们的回归模型，我们需要确保模型处理新数据的能力与处理训练数据的能力一样好。为此，我们需要使用测试数据调用损失和度量组合的测试方法，如下所示 -

loss.test([X_test, y_test])

输出−

{'metric': 1.89679785619, 'samples': 79}