电力电子 - 斩波器

斩波器使用高速连接和断开源负载。通过连续触发电源开关的开/关，将固定的直流电压间歇地施加到源负载。电源开关保持ON或OFF的时间段分别称为斩波器的ON和OFF状态时间。

斩波器主要应用于电动汽车、风能、太阳能转换、直流电机调节器等领域。

斩波器的象征

斩波符号

斩波器的分类

根据电压输出，斩波器分为 -

  • 升压斩波器（升压转换器）
  • 降压斩波器（降压转换器）
  • 升压/降压斩波器（降压-升压转换器）

升压斩波器

升压斩波器中的平均电压输出 (V o ) 大于电压输入 (V s )。下图显示了升压斩波器的配置。

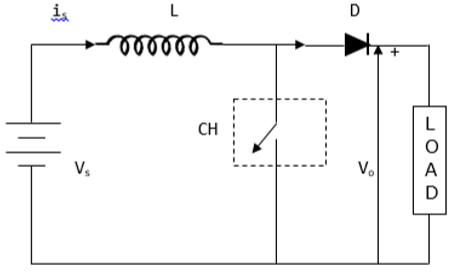
升压斩波器

电流和电压波形

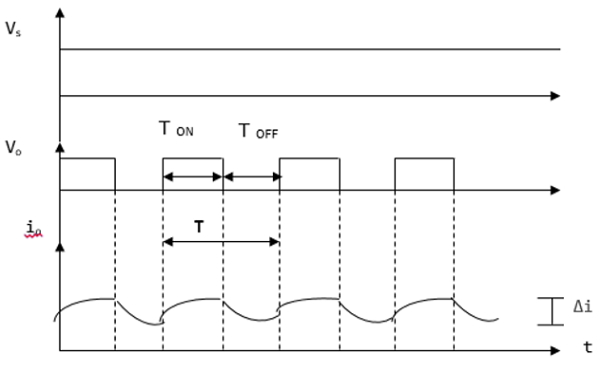
当斩波器打开时， V 0（平均电压输出）为正，当斩波器关闭时，V 0 （平均电压输出）为负，如下波形所示。

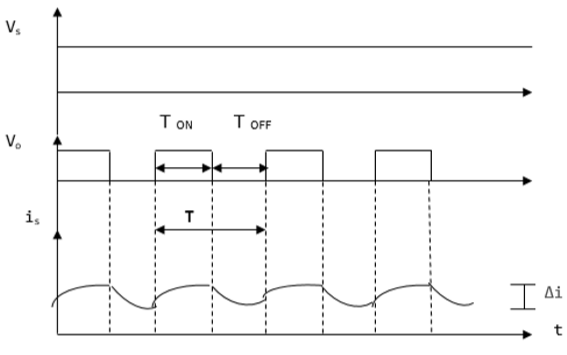
电流电压波形

在哪里

T ON – 斩波器开启的时间间隔

T OFF – 斩波器关闭的时间间隔

V L – 负载电压

V s – 源电压

T – 斩波时间周期 = T ON + T OFF

V o由下式给出 -

$$V_{0}=\frac{1}{T}\int_{0}^{T_{ON}}V_{S}dt$$

当斩波器（CH）接通时，负载短路，因此，T ON期间的电压输出为零。另外，电感器在此期间被充电。这给出 V S = V L

$L\frac{di}{dt}=V_{S},$ $\frac{\Delta i}{T_{ON}}=\frac{V_{S}}{L}$

因此，$\Delta i=\frac{V_{S}}{L}T_{ON}$

Δi = 是电感峰峰值电流。当斩波器 (CH) 关闭时，通过电感器 L 发生放电。因此，V s和 V L的总和如下 -

$V_{0}=V_{S}+V_{L},\quad V_{L}=V_{0}-V_{S}$

但$L\frac{di}{dt}=V_{0}-V_{S}$

因此，$L\frac{\Delta i}{T_{OFF}}=V_{0}-V_{S}$

由此得出$\Delta i=\frac{V_{0}-V_{S}}{L}T_{OFF}$

将 ON 状态下的 Δi 等于 OFF 状态下的 Δi 得出 -

$\frac{V_{S}}{L}T_{ON}=\frac{V_{0}-V_{S}}{L}T_{OFF}$, $V_{S}\left ( T_{ ON }+T_{关闭} \右)=V_{0}T_{关闭}$

$V_{0}=\frac{TV_{S}}{T_{OFF}}=\frac{V_{S}}{\frac{\left ( T+T_{ON} \right )}{T}} $

平均电压输出为：

$$V_{0}=\frac{V_{S}}{1-D}$$

上式表明，V o可以在 V S到无穷大之间变化。它证明输出电压始终大于输入电压，因此它会升高或增加电压电平。

降压斩波器

这也称为降压转换器。在该斩波器中，平均电压输出V O小于输入电压V S。当斩波器打开时，V O = V S；当斩波器关闭时，V O = 0

当斩波器打开时 -

$V_{S}=\left ( V_{L}+V_{0} \right ),\quad V_{L}=V_{S}-V_{0},\quad L\frac{di}{dt} =V_{S}-V_{0},\quad L\frac{\Delta i}{T_{ON}}=V_{s}+V_{0}$

因此，峰峰值电流负载由下式给出：

$\Delta i=\frac{V_{s}-V_{0}}{L}T_{ON}$

电路原理图

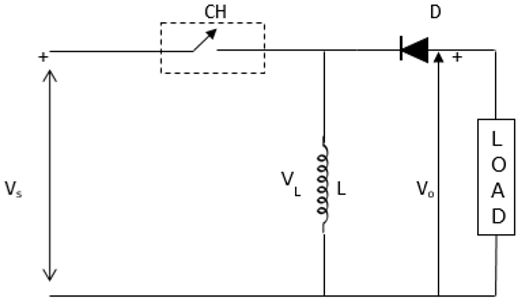
电路原理图

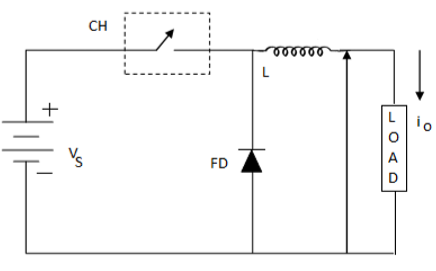
其中FD为续流二极管。

当斩波器关闭时，电感器会发生极性反转和放电。电流通过续流二极管和电感到达负载。这给出了，

$$L\frac{di}{dt}=V_{0}................................ ......\左（我\右）$$

重写为 -$\quad L\frac{\Delta i}{T_{OFF}}=V_{0}$

$$\Delta i=V_{0}\frac{T_{OFF}}{L}........................ ......\左 ( ii \右 )$$

将等式 (i) 和 (ii) 等式得出：

$\frac{V_{S}-V_{0}}{L}T_{ON}=\frac{V_{0}}{L}T_{OFF}$

$\frac{V_{S}-V_{0}}{V_{0}}=\frac{T_{OFF}}{T_{ON}}$

$\frac{V_{S}}{V_{0}}=\frac{T_{ON}-T_{OFF}}{T_{ON}}$

上式给出：

$$V_{0}=\frac{T_{ON}}{T}V_{S}=DV_{S}$$

方程 (i) 给出 -

$\Delta i=\frac{V_{S}-DV_{S}}{L}DT$，来自 $D=\frac{T_{ON}}{T}$

$=\frac{V_{S}-\left ( 1-D \right )D}{Lf}$

$f=\frac{1}{T}=$斩波频率

电流和电压波形

电流和电压波形如下 -

对于降压斩波器，电压输出始终小于电压输入。下面的波形显示了这一点。

电流和电压波形

升压/降压斩波器

这也称为降压-升压转换器。它可以增加或减少电压输入电平。下图显示了降压-升压斩波器。

降压斩波器

当斩波器接通时，电感器 L 被源电压 V s充电。因此，V s = V L。

$$L\frac{di}{dt}=V_{S}$$ $$\Delta i=\frac{V_{S}}{L}T_{ON}=\frac{V_{S}}{L }T\frac{T_{ON}}{T}=\frac{DV_{S}}{Lf}$$

因为 -

$D=\frac{T_{ON}}{T}$ 和$f=\frac{1}{T} ........................ ......................\左 ( iii \右 )$

当斩波器关闭时，电感器的极性反转，这导致它通过二极管和负载放电。

因此，

$$V_{0}=-V_{L}$$ $$L\frac{di}{dt}=-V_{0}$$

$L\frac{\Delta i}{T_{OFF}}=-V_{0}$，因此$\Delta i=-\frac{V_{0}}{L}T_{OFF}..... ......................\左 ( iv \右 )$

评估方程 (iii) 和 (iv) 得出 -

$\frac{DV_{S}}{Lf}=-\frac{V_{0}}{L}T_{关闭}$, $DV_{S}=-DV_{S}=-V_{0}T_{关}f$

$DV_{S}=-V_{0}\frac{T-T_{ON}}{T}=-V_{0}\left ( 1-\frac{T_{ON}}{T} \right )$ , $V_{0}=-\frac{DV_{S}}{1-D}$

因为$D=\frac{T_{ON}}{T}=\frac{T-T_{OFF}}{1-D}$

这给出了，

$V_{0}=\frac{DV_{S}}{1-D}$

D可以在0到1之间变化。当D=0时；VO = 0

当D = 0.5时，V O = V S

当D = 1时，V O = ∞。

因此，在 0 ≤ D ≤ 0.5 区间内，输出电压在 0 ≤ V O < V S范围内变化，我们得到降压或降压操作。而在 0.5 ≤ D ≤ 1 区间内，输出电压在 V S ≤ V O ≤ ∞范围内变化，我们得到升压或升压操作。