
- 电力电子教程
- 电力电子 - 首页
- 电力电子 - 简介
- 电力电子 - 开关器件
- 线性电路元件
- 直流到直流转换器
- 电力电子 - 斩波器
- 电力电子 - 控制方法
- 谐振开关
- 直流转换器解决示例
- 交流转直流转换器
- 单相交流电压控制器
- 电力电子 - 环路转换器
- 积分循环控制
- 电力电子 - 矩阵转换器
- 解决的例子
- 电力电子资源
- 电力电子 - 快速指南
- 电力电子 - 有用资源
- 电力电子 - 讨论
电力电子 - 快速指南
电力电子 - 简介
电力电子是指控制电流和电压流动并将其转换为适合用户负载的形式的过程。最理想的电力电子系统是效率和可靠性为 100% 的电力电子系统。
看一下下面的框图。它显示了电力电子系统的组件以及它们如何相互关联。
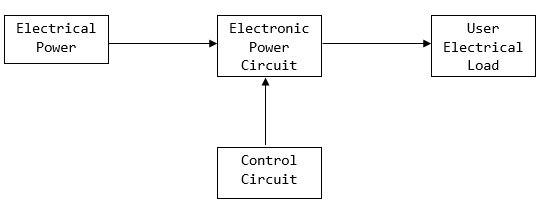
电力电子系统将电能从一种形式转换为另一种形式,并确保实现以下目标 -
- 最高效率
- 最大可靠性
- 最大可用性
- 最低成本
- 重量最轻
- 小尺寸
电力电子应用分为两种类型:静态应用和驱动应用。
静态应用
这利用了移动和/或旋转机械部件,例如焊接、加热、冷却、电镀和直流电源。
直流电源

驱动应用
驱动应用具有旋转部件,例如电机。例如压缩机、泵、传送带和空调系统。
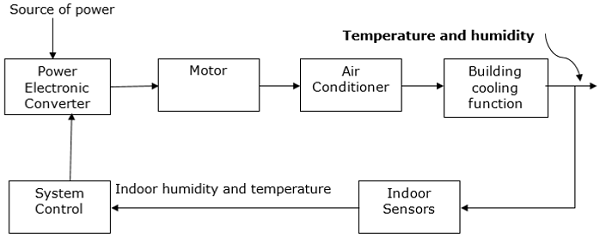
空调系统
电力电子技术广泛应用于空调中以控制压缩机等元件。下图显示了电力电子技术在空调中的应用原理图。
电力电子 - 开关器件
电力电子开关器件是集成有源可开关电力半导体驱动器的组合。交换机的主要特性是由其集成系统功能的内部关联和相互作用决定的。下图显示了电力电子开关系统的工作原理。

上图的外部电路通常相对于控制单元保持在高电位。电感式发射器用于支持两个接口之间所需的电位差。
功率开关器件通常根据其处理功率的额定值来选择,即其电流和电压额定值的乘积,而不是其功耗率。因此,电力电子开关的主要吸引力特征是其能够消耗低功率或几乎不消耗功率。结果,电子开关能够实现低且连续的浪涌功率。
电力电子 - 线性电路元件
线性电路元件是指电路中电流输入和电压输出之间呈现线性关系的元件。具有线性电路的元件示例包括 -
- 电阻器
- 电容器
- 电感器
- 变形金刚
为了更好地理解线性电路元件,有必要对电阻元件进行分析。
电阻器
电阻器是一种限制电流流动从而实现能量转换的装置。例如,当电流流过灯泡时,电流被转换成不同形式的能量,例如热和/或光。元件的电阻以欧姆 (Ω) 为单位测量。
给定电路中电阻的测量由下式给出 -
$$R=\rho \frac{L}{A}$$其中R——电阻;ρ——电阻率;L——导线长度;A - 导线的横截面积
各种电阻的符号
| 电阻器 | 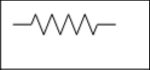 |
| 可变电阻器 | 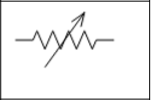 |
| 电位器一个 | 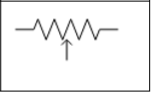 |
电容器
电容器是指一种电气设备,具有两种导电材料(也称为板),并被称为电介质的绝缘体隔开。它利用电场来储存电能。当电容器连接到电池时会产生电场,从而使正电荷积聚在一个板上,而负电荷积聚在另一板上。
当能量存储在电容器的电场中时,该过程称为充电,而当能量被移除时,该过程称为放电。电容器中存储的电能水平称为电容,以法拉 (F) 为单位。一法拉等于每单位伏特一库仑,由 1 C/V 给出。
电容器和电池之间的区别在于电容器存储电能,而电池存储化学能并以缓慢的速率释放能量。
各种电容器的符号
下表给出了电容器的各种符号。
| 固定电容 | 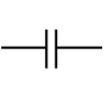 |
| 可变电容器 | 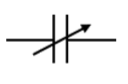 |
| 极化电容器 | 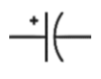 |
电感器
电感器是利用磁场来储存电能的电子器件。电感器最简单的形式是线圈或环形导线,其中电感与导线中的环数成正比。此外,电感取决于导线中材料的类型和环路的半径。
给定一定的匝数和半径大小,只有空芯才能产生最小的电感。与空气具有相同用途的介电材料包括木材、玻璃和塑料。这些材料有助于绕制电感器的过程。绕组的形状(环形)以及铁磁物质(例如铁)会增加总电感。
电感器可以存储的能量称为电感。它以亨利 (H) 为单位进行测量。
各种电感的符号
| 固定电感 | 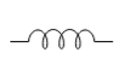 |
| 可变电感器 |  |
变形金刚
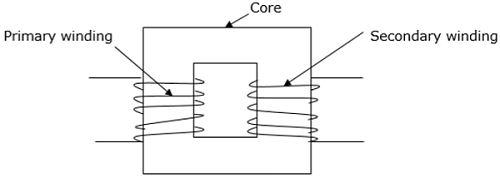
这是指通过电磁感应过程将能量从一个水平改变到另一个水平的装置。它通常用于在利用电力的应用中升高或降低交流电压。
当变压器初级侧的电流变化时,其磁芯上会产生变化的磁通量,该磁通量以磁场的形式传播到变压器的次级绕组。
变压器的工作原理依赖于法拉第电磁感应定律。该定律指出,磁通相对于时间的变化率与导体中感应的电动势直接相关。
变压器由三个主要部分组成 -
- 初级绕组
- 磁芯
- 次级绕组
变压器的符号
附加设备
电磁装置
电磁学的概念在科技领域应用广泛,应用于电动机、发电机和电铃等。例如,在门铃中,电磁组件会吸引一个拍板,撞击门铃并使其响起。
控制器
控制器是接收过程中从测量变量传输的电子信号并将获得的值与控制设定点进行比较的设备。它利用数字算法来关联和比较函数。
传感器
传感器用于确定电流,电流不断变化以提供控制目的反馈。感测电流使得实现平滑且精确的转换器功能成为可能。电流传感器在转换器中至关重要,因此可以轻松共享并联或多相转换器中的信息。
过滤器
电子滤波器还用于对信号进行处理以消除不需要的频率。它们是模拟电路,以主动或被动状态存在。
可控硅
可控硅或半导体控制整流器是一种四层固态电流控制器件。“硅控整流器”这个名称是通用电气对一种晶闸管的商品名称。
SCR主要用于需要控制高电压和功率的电子设备中。这使得它们适用于中高交流功率操作,例如电机控制功能。
当向 SCR 施加栅极脉冲时,SCR 就会导通,就像二极管一样。它有四层半导体,形成两种结构:NPNP 或 PNPN。此外,它还具有标记为 J1、J2 和 J3 的三个结点和三个端子(阳极、阴极和栅极)。SCR 的示意图如下所示。

阳极连接到 P 型,阴极连接到 N 型,栅极连接到 P 型,如下所示。

在 SCR 中,本征半导体是硅,其中注入了所需的掺杂剂。然而,PNPN 结的掺杂取决于 SCR 应用。
SCR 的运行模式
关闭状态(正向阻断模式) - 这里,阳极被分配正电压,栅极被分配零电压(断开),阴极被分配负电压。因此,结点 J1 和 J3 处于正向偏置,而 J2 处于反向偏置。J2 达到其击穿雪崩值并开始导通。低于该值时,J1 的电阻非常高,因此处于关闭状态。
ON 状态(导电模式) - 通过将阳极和阴极之间的电位差增加到雪崩电压以上或在栅极施加正信号,使 SCR 进入此状态。SCR 立即开始导通,不再需要栅极电压来维持导通状态,因此通过 -
将流过它的电流减少到称为保持电流的最低值
使用跨接点放置的晶体管。
反向阻断 - 这可以补偿正向电压的下降。这是因为 P1 中需要低掺杂区域。需要注意的是,正向和反向阻断的额定电压是相等的。
电力电子 - TRIAC
缩写词 TRIAC 代表交流三极管。TRIAC 是一种具有三个端子的半导体器件,可控制电流的流动,因此得名 Triac。与 SCR 不同,TRIAC 是双向的,而 SCR 是双向的。它非常适合利用交流电源进行开关操作,因为它可以控制交流周期中两半的电流。下图中清楚地解释了这一点。

双向晶闸管符号
TRIAC 的电路图如下所示。它类似于两个背靠背放置的晶闸管。

可控硅结构
TRIAC结构被认为是具有额外栅极接触以确保器件控制的DIAC。与其他功率器件类似,TRIAC 由硅制成。因此,制造硅的过程可以生产出更便宜的设备。如下所示,TRIAC 有六个区域,即:四个N型区域和两个P型区域。

双向晶闸管操作
TRIAC 的操作基于晶闸管。它有助于交流电气元件和系统的开关功能。它们广泛用于调光器,因为它们允许利用交流周期的两半。因此,这使得它们的电力使用效率更高。尽管可以使用晶闸管充当 TRIAC,但对于需要低功率的操作来说,它并不具有成本效益。可以将 TRIAC 视为两个晶闸管。

TRIAC 通常用于不需要很高功率的应用,因为它们在运行中表现出非对称开关。这对于使用高功率的应用来说是不利的,因为它会引起电磁干扰。因此,TRIAC 可用于电机控制、轻型住宅调光器和小型电风扇来控制速度。
电力电子 - BJT
双极结型晶体管 (BJT) 是一种其工作取决于两个半导体的接触的晶体管。它可以充当开关、放大器或振荡器。它被称为双极晶体管,因为它的运行需要两种类型的电荷载流子(空穴和电子)。空穴构成P型半导体中的主要电荷载体,而电子是N型半导体中的主要电荷载体。
BJT 的符号

BJT 的结构
BJT 有两个背靠背连接的 PN 结,并共享公共区域 B(基极)。这确保了基极、集电极和发射极的所有区域均形成接触。PNP双极晶体管的结构如下所示。

上图所示的 BJT 由两个背对背连接的二极管组成,导致称为准中性区域的耗尽。发射极、基极和集电极的准中性线宽度在上面表示为W E '、W B '和W C '。它们的获得如下 -
$$W_{E}^{'}=W_{E}-X_{n,BE}$$ $$W_{B}^{'}=W_{B}-X_{p,BE}-X_{p ,BC}$$ $$W_{C}^{'}=W_{C}-X_{n,BC}$$发射极、基极和集电极电流的常规符号分别用IE 、 IB和IC表示。因此,当正电流遇到集电极或基极接触时,集电极和基极电流为正。此外,当电流离开发射极触点时,发射极电流为正。因此,
$$I_{E}=I_{B}+I_{C}$$当相对于集电极和发射极的基极触点施加正电压时,基极-集电极电压以及基极-发射极电压变为正。
为简单起见,假设V CE为零。
电子扩散从发射极到基极,而空穴扩散从基极到发射极。一旦电子到达基极-集电极耗尽区域,它们就会被电场扫过该区域。这些电子形成集电极电流。
当 BJT 在正向有源模式下偏置时,总发射极电流通过将电子扩散电流 ( I E,n )、空穴扩散电流 ( I E, p ) 和基极发射极电流相加获得。
$$I_{E}=I_{E,n}+I_{E,p}+I_{r,d}$$总集电极电流由电子扩散电流 ( I E,n ) 减去基极复合电流 ( I r,B ) 得出。
$$I_{C}=I_{E,n}-I_{r,B}$$基极电流I B的总和是通过将空穴扩散电流( IE ,p )、基极复合电流( Ir ,B )和耗尽层基极-发射极复合电流( Ir ,d )相加得到的。
$$I_{B}=I_{E,p}+I_{r,B}+I_{r,d}$$运输因素
这是由集电极电流和发射极电流之比给出的。
$$\alpha =\frac{I_{C}}{I_{E}}$$应用基尔霍夫电流定律,发现基极电流由发射极电流和集电极电流之差给出。
电流增益
这是由集电极电流与基极电流之比给出的。
$$\beta =\frac{I_{C}}{I_{B}}=\frac{\alpha }{1-\alpha }$$上面解释了BJT如何产生电流放大。如果集电极电流几乎等于发射极电流,则传输因子 (α) 接近 1。电流增益(β)因此变得大于1。
为了进一步分析,传输因子(α)被重写为发射极效率(γ E)、基极传输因子(α T)和耗尽层复合因子(δ r)的乘积。它被重写如下 -
$$\alpha =\gamma _{E}\times \alpha _{T}\times \delta _{r}$$以下是所讨论的发射极效率、基极传输因子和耗尽层复合因子的总结。
发射极效率
$$\gamma_{E}=\frac{I_{E,n}}{I_{E,p}+I_{E,P}}$$基本传输因子
$$\alpha _{T}=\frac{I_{E,n}-I_{r,b}}{I_{E,n}}$$耗尽层复合因子
$$\delta _{r}=\frac{I_{E}-I_{r,d}}{I_{E,n}}$$电力电子 - IGBT
绝缘栅双极晶体管(IGBT)是一种三端子半导体器件,主要用作电子开关。它具有快速开关和高效率的特点,这使其成为灯镇流器、电动汽车和变频驱动器(VFD)等现代电器的必备组件。
它快速打开和关闭的能力使其适用于放大器,通过脉宽调制处理复杂的波形。IGBT 结合了 MOSFET 和 BJT 的特性,分别具有高电流和低饱和电压能力。它集成了一个使用 FET(场效应晶体管)的隔离栅极以获得控制输入。
IGBT符号

IGBT 的放大倍数通过其输出信号与其输入信号的比率来计算。在传统 BJT 中,增益 (β) 等于其输出电流与输入电流之比。
与 MOSFET 相比,IGBT 的导通电阻 (RON) 值非常低。这意味着对于特定开关操作,双极两端的电压降 (I 2 R) 非常低。IGBT 的正向阻断作用与 MOSFET 类似。
当 IGBT 在静态下用作受控开关时,其额定电流和电压与 BJT 相同。相反,IGBT 中的隔离栅极更容易驱动 BJT 电荷,因此所需的功率更少。
IGBT 根据其栅极端子是否已激活或停用而导通或关断。栅极和发射极之间恒定的正电位差使 IGBT 保持在导通状态。当输入信号移除时,IGBT 关闭。
IGBT 工作原理
与 BJT 不同,IGBT 只需很小的电压即可维持器件导通。IGBT是单向器件,即只能正向导通。这意味着电流从集电极流向发射极,与 MOSFET 不同,MOSFET 是双向的。
IGBT的应用
IGBT 用于中等到超高功率应用,例如牵引电机。在大型 IGBT 中,可以处理数百安培范围内的大电流和高达 6kv 的阻断电压。
IGBT 还用于电力电子设备,例如转换器、逆变器和其他需要固态开关的设备。双极性晶体管可提供高电流和高电压。然而,它们的切换速度较低。相反,MOSFET 尽管价格昂贵,但开关速度较高。
电力电子器件 - MOSFET
金属氧化物半导体场效应晶体管 (MOSFET) 是一种用于开关电子信号的晶体管。它有四个航站楼,即:源极 (S)、漏极 (D)、栅极 (G) 和体 (B)。MOSFET 的体通常连接到源极 (S) 端子,这导致类似于其他场效应晶体管的三端器件(场效应管)。由于这两个主端子通常通过短路互连,因此在电气图中只能看到三个端子。
它是数字和模拟电路中最常见的设备。与常规晶体管相比,MOSFET 需要低电流(小于一毫安)即可导通。同时,它可提供超过 50 安培的高电流负载。
MOSFET 的操作
MOSFET 有一层薄薄的二氧化硅,充当电容器的极板。控制栅极的隔离将 MOSFET 的电阻提高到极高水平(几乎无穷大)。
栅极端子被阻止进入初级电流通路;因此,没有电流泄漏到栅极。
MOSFET 有两种主要形式 -
耗尽状态- 这需要栅源电压 (V GB ) 来关闭组件。当栅极为零 (V GB ) 时,器件通常处于导通状态,因此,它充当给定逻辑电路的负载电阻。对于具有 N 型耗尽的负载器件,3V 是通过将栅极切换到负 3V 来关闭器件的阈值电压。
增强状态- 在此状态下需要栅源电压 (V GB ) 才能打开组件。当栅极为零 (V GB ) 时,器件通常处于关闭状态,并且可以通过确保栅极电压高于源电压来打开。
符号和基本结构

其中,D——漏极;G——门;S-源;和子- 基板
功率半导体器件解决了Ex
A (BJT) 发射电流为 1mA,发射极效率为 0.99。基本传输因子为0.994,耗尽层复合因子为0.997。对于 BJT,计算如下 -
运输因素
重写的传输因子由下式给出 -
$$\alpha =\gamma _{E}\times \alpha _{T}\times \delta _{r}$$代入数值,我们得到
$$\alpha =0.99\乘以0.994\乘以0.997=0.981$$当前增益
电流增益由下式给出 -
$$\beta =\frac{I_{C}}{I_{B}}=\frac{\alpha }{1-\alpha }$$代入数值,我们得到
$$\beta =\frac{0.981}{1-0.981}=51.6$$集电极电流
$$I_{C}=\alpha \乘I_{E}=0.981\乘1=0.981mA$$基极电流
$$I_{B}=I_{E}-I_{C}=1-0.981=19\mu A$$电力电子 - 脉冲转换器
相控转换器
相控转换器将交流电转换为直流电(线换向)。换句话说,它用于将固定频率、固定电压的交流电转换为可变的直流电压输出。其表示为
固定输入- 电压、频率和交流电源
可变输出-直流电压输出
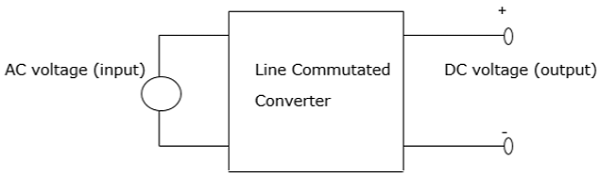
进入转换器的交流输入电压通常具有固定的 RMS(均方根)和固定的频率。转换器中包含相控晶闸管可确保获得可变的直流输出电压。这是通过改变晶闸管触发的相位角来实现的。结果,获得负载电流的脉动波形。
在输入电源半周期期间,晶闸管处于正向偏置状态,并通过施加足够的栅极脉冲(触发)而导通。一旦晶闸管导通,即在点 ωt=α 到点 ωt=β 处,电流就开始流动。当负载电流降至零时,晶闸管会因线路(自然)换相而关闭。
有许多利用自然换向的电源转换器。这些包括 -
- 交流转直流转换器
- 交流至交流转换器
- 交流电压控制器
- 环路转换器
上述电源转换器将在本教程的后续章节中进行解释。
2-脉冲转换器
两相脉冲转换器,也称为二级脉宽调制器 (PWM) 发生器,用于为基于载波的脉宽调制转换器生成脉冲。它通过利用二级拓扑来实现这一点。该块控制用于控制目的的开关器件,例如存在于三种类型转换器中的 IGBT 和 FET,即 -
- 1臂(单相半桥)
- 2臂(单相全桥)
- 3臂(三相桥)
2 脉冲转换器中的参考输入信号与载波进行比较。如果参考输入信号大于载波,则上位设备的脉冲等于1,下位设备的脉冲等于0。
为了控制具有单相全桥(2臂)的设备,需要应用单极或双极脉宽调制。在单极调制中,两个臂中的每一个都是独立控制的。第二个参考输入信号是通过将初始参考点偏移 180° 在内部生成的
当应用双极PWM时,第二单相全桥中的下开关器件的状态与第一单相全桥器件中的上开关器件的状态类似。使用单极调制可以产生平滑的交流波形,而双极调制则可以产生较小的电压变化。
3脉冲转换器
考虑一个三相 3 脉冲转换器,其中每个晶闸管在供电周期的第三个周期内都处于导通模式。晶闸管最早被触发导通的时间是相对于相电压的 30°。
使用三个晶闸管和三个二极管来解释其操作。当将晶闸管T1、T2和T3替换为二极管D1、D2和D3时,将分别在相对于相电压u an 、u bn和u cn成30°的角度处开始导通。因此,初始测量的触发角α相对于与其对应的相电压为30°。
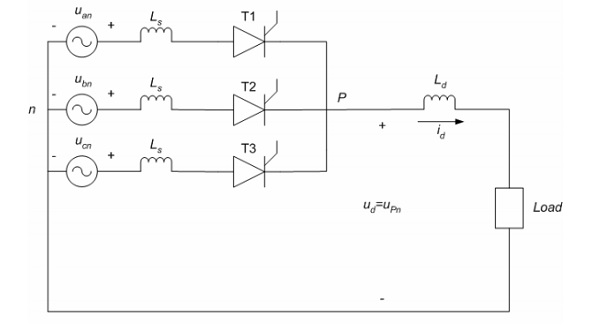
电流只能沿一个方向流过晶闸管,这类似于逆变器的工作模式,功率从直流侧流向交流侧。此外,晶闸管中的电压是通过控制触发角来控制的。当 α = 0(可能在整流器中)时可以实现这一点。因此,3脉冲转换器充当逆变器和整流器。
6脉冲转换器
下图显示了连接到三相电源的六脉冲桥式控制转换器。在该转换器中,脉冲数是相数的两倍,即p = 2m。使用相同的转换器配置,可以组合两个六脉冲电桥以获得十二个或更多脉冲转换器。
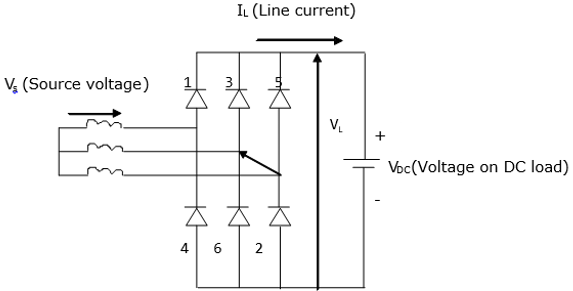
当换向不可用时,两个二极管将在任何特定时间导通。此外,为了获得负载两端的压降,两个二极管必须位于电桥的相对腿上。例如,二极管3和6不能同时导通。因此,直流负载上的电压降是来自三相电源的线电压 VL 的组合。
值得注意的是,脉冲数量越多,转换器的利用率就越高。此外,脉冲数量越少,转换器的利用率就越低。
源电感的影响
大多数转换器的分析通常在理想条件(无源阻抗)下得到简化。然而,这种假设是不合理的,因为源阻抗通常是感性的,电阻元件可以忽略不计。
源电感对转换器性能有重大影响,因为它的存在会改变转换器的输出电压。结果,输出电压随着负载电流的减小而减小。此外,输入电流和输出电压波形也发生显着变化。
源电感对转换器的影响可以通过以下两种方式进行分析。
对单相的影响
假设转换器在导通模式下工作,并且负载电流的纹波可以忽略不计,则开路电压等于触发角 α 时的平均直流输出。下图显示了单相电源的完全控制转换器。当 t = 0 时,假定晶闸管 T 3和 T 4处于导通模式。另一方面,当 ωt = α 时,T 1和 T 2触发

其中 -
- Vi =输入电压
- I i = 输入电流
- V o = 输出电压
- I o = 输出电压
当没有源极电感时,换相将发生在T 3和T 4处。晶闸管 T 1和 T 2立即接通。这将导致输入极性瞬间改变。在存在源极电感的情况下,极性和换向的改变不会立即发生。因此,一旦T 1和T 2接通,T 3和T 4就不会换向。
在某个时间间隔内,所有四个晶闸管都会导通。该导电间隔称为重叠间隔(μ)。
换相过程中的重叠会降低直流输出电压和消光角γ,导致当α接近180°时换相失败。下面的波形显示了这一点。

对三相的影响
就像单相转换器一样,由于源电感的存在,不存在瞬时换向。考虑到源电感,对转换器性能的影响(定性)与单相转换器相同。如下图所示。

电力电子-性能参数
确定拓扑结构可以是单相或多相的不同转换器的性能参数非常重要。
假设
- 使用的设备是理想的,即它们没有任何损耗
- 该设备具有电阻负载

负载上的直流电压
$$V_{DC}=\frac{1}{T} \int_{0}^{T}V_{L}\left ( t \right )dt$$负载上的有效电压
$$V_{L}=\sqrt{\frac{1}{T}}\int_{0}^{T}V_{L}^{2}\left ( t \right )dt$$构成因素
$$FF=\frac{V_{L}}{V_{DC}}$$纹波系数
$$RF=\frac{\sqrt{V_{L}^{2}-V_{DC}^{2}}}{V_{DC}}=\sqrt{FF^{2}-1}$$效率(整流系数)
$$\eta =\frac{P_{DC}}{P_{L}+P_{D}}$$其中上述定义为 -
$P_{DC}=V_{DC}\times I_{DC}$
$P_{L}=V_{L}\times I_{L}$
$P_{D}=R_{D}\times I_{L}^{2}$($P_{D}$为整流器损耗,$R_{D}$为电阻)
$$\eta =\frac{V_{DC}I_{DC}}{\left ( V_{L}I_{L} \right )+\left ( R_{D}I_{L}^{2} \right )}=\frac{V_{DC}^{2}}{V_{L}^{2}}\times \frac{1}{1+\frac{R_{D}}{R_{L}}} $$但是$R_{D}=0$
所以,
$$\eta =\left ( \frac{V_{DC}}{V_{L}} \right )^{2}=\left ( \frac{1}{FF}\right )^{2}$$变压器利用率
$$TUF=\frac{P_{DC}}{VA \:变压器的额定值}=\frac{P_{DC}}{\frac{VA_{p}+VA_{s}} {2}}$$VA p和 VA s是变压器的初级和次级额定功率。
变流器的无功功率控制
在高压直流 (HVDC) 变流器中,站点采用线路换向。这意味着阀的初始电流只能以交流形式的转换器总线电压的零值为参考来延迟。因此,为了更好地控制电压,转换器总线连接到无功电源。
无功电源用于改变静态系统中的电容器。无功电力系统的响应由动态条件下的电压控制决定。
当运行不稳定的交流系统时,往往会因电压不稳定和过压浪涌而出现问题。需要更好地协调无功电源以简化触发角的控制。因此,无功功率转换器的这一特性越来越多地应用于使用 HVDC 的现代转换器中。
稳态无功功率控制
将无功功率表示为有功功率函数的方程以单位量的形式给出。
基础转换器电压由下式给出 -
$$V_{db}=3\sqrt{\frac{2}{\pi }}\times V_{L}$$其中V L = 线间电压(绕组侧)
基本直流电流 (I db ) = 额定直流电流(I dr )
基本直流功率 (P dc ) = n b × V db × I db,其中n b = 串联电桥数量
基极交流电压 (V b ) = (V a )
基本交流电源= 基本直流电源
$$\sqrt{\frac{18}{\pi }}\乘以V_{a}\乘以I_{db}\乘以n_{b}$$电力电子 - 双转换器
双转换器主要用于变速驱动器 (VFD)。在双转换器中,两个转换器背靠背连接在一起。使用下图解释双转换器的操作。假设 -
双转换器是一种理想的转换器(在其端子处提供纯直流输出)。
每个两象限转换器都是与二极管串联的受控直流源。
二极管D1和D2显示电流的单向流动。
考虑到双转换器在没有循环电流的情况下运行,交流电流被受控发射脉冲阻止流动。这确保了承载负载电流的转换器导通,而另一个转换器被阻断。这意味着转换器之间不需要电抗器。

充电器
电池充电器也称为充电器,利用电流将能量存储在蓄电池中。充电过程由电池的类型和尺寸决定。不同类型的电池对过度充电的耐受程度不同。充电过程可以通过连接恒压或恒流源来实现。
充电速率(C)
充电速率定义为电池充电或放电的速率,等于一小时内电池的容量。
电池充电器以其充电速率 C 来指定。例如,额定值为 C/10 的电池充电器可在 10 小时内充满电,而额定值 3C 的电池充电器可在 20 分钟内充满电。
电池充电器的类型
电池充电器有多种类型。在本教程中,我们将考虑五种主要类型。
简单的充电器- 通过向正在充电的电池提供恒定的直流电源来运行。
快速充电器- 使用控制电路对电池快速充电,并在此过程中防止电池损坏。
感应充电器- 使用电磁感应为电池充电。
智能充电器- 用于为包含与智能充电器通信的芯片的电池充电。
运动供电充电器- 利用人体运动为电池充电。放置在两个弹簧之间的磁铁通过人体运动上下移动,从而为电池充电。
相控转换器解决示例
他励直流电机的参数如下:220V、100A、1450rpm。其电枢的电阻为0.1Ω。此外,它由连接到频率为 50 Hz、感抗为 0.5 Ω 和 50 Hz 的三相交流电源的三相全控转换器供电。当 α = 0 时,电机以额定扭矩和速度运行。假设电机以其额定速度使用相反方向再生制动。计算不影响换向的最大电流。
解决方案-
我们知道,
$$V_{db}=3\sqrt{\frac{2}{\pi }}\times V_{L}-\frac{3}{\pi }\times R_{b}\times I_{db}$ $代入这些值,我们得到,
$220=3\sqrt{\frac{2}{\pi }}\times V_{L}-\frac{3}{\pi }\times 0.5\times 100$
所以,
$V_{L}=198V$
额定转速电压 = $220-\left ( 100\times 0.1 \right )=210V$
在额定速度下,反向再生制动,
$=3\sqrt{\frac{2}{\pi }}\times 198\cos \alpha -\left ( \frac{3}{\pi }\times 0.5+0.1\right )\times I_{db} =-210V$
但$\cos \alpha -\cos \left ( \mu +\alpha \right )=\frac{\sqrt{2}}{198}\times 0.5I_{db}$
要使换相失败,应满足以下限制条件。
$\mu +\alpha \约180^{\circ}$
因此,$\quad \cos \alpha =\frac{I_{db}}{198\sqrt{2}}-1$
还,
$\frac{3}{\pi }I_{db}-\frac{3\sqrt{2}}{\pi }\times 198-\left ( \frac{3}{\pi }\times 0.5+0.1 \右)I_{db}=-210$
这给出 $\quad 0.3771I_{db}=57.4$
因此,$\quad I_{db}=152.2A$
电力电子 - 斩波器
斩波器使用高速连接和断开源负载。通过连续触发电源开关的开/关,将固定的直流电压间歇地施加到源负载。电源开关保持ON或OFF的时间段分别称为斩波器的ON和OFF状态时间。
斩波器主要应用于电动汽车、风能、太阳能转换、直流电机调节器等领域。
斩波器的象征
斩波器的分类
根据电压输出,斩波器分为 -
- 升压斩波器(升压转换器)
- 降压斩波器(降压转换器)
- 升压/降压斩波器(降压-升压转换器)
升压斩波器
升压斩波器中的平均电压输出 (V o ) 大于电压输入 (V s )。下图显示了升压斩波器的配置。
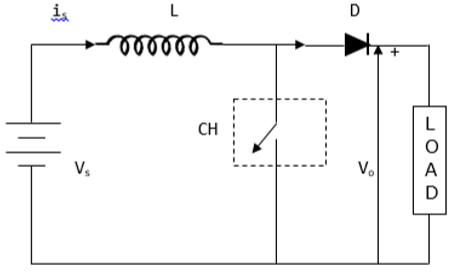
电流和电压波形
当斩波器打开时, V 0(平均电压输出)为正,当斩波器关闭时,V 0 (平均电压输出)为负,如下波形所示。
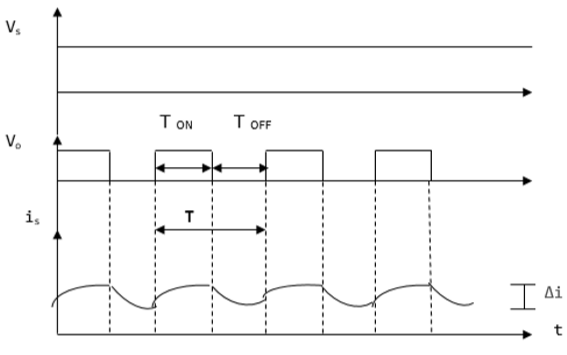
在哪里
T ON – 斩波器开启的时间间隔
T OFF – 斩波器关闭的时间间隔
V L – 负载电压
V s – 源电压
T – 斩波时间周期 = T ON + T OFF
V o由下式给出 -
$$V_{0}=\frac{1}{T}\int_{0}^{T_{ON}}V_{S}dt$$当斩波器(CH)接通时,负载短路,因此,T ON期间的电压输出为零。另外,电感器在此期间被充电。这给出 V S = V L
$L\frac{di}{dt}=V_{S},$ $\frac{\Delta i}{T_{ON}}=\frac{V_{S}}{L}$
因此,$\Delta i=\frac{V_{S}}{L}T_{ON}$
Δi = 是电感峰峰值电流。当斩波器 (CH) 关闭时,通过电感器 L 发生放电。因此,V s和 V L的总和如下 -
$V_{0}=V_{S}+V_{L},\quad V_{L}=V_{0}-V_{S}$
但$L\frac{di}{dt}=V_{0}-V_{S}$
因此,$L\frac{\Delta i}{T_{OFF}}=V_{0}-V_{S}$
由此得出$\Delta i=\frac{V_{0}-V_{S}}{L}T_{OFF}$
将 ON 状态下的 Δi 等于 OFF 状态下的 Δi 得出 -
$\frac{V_{S}}{L}T_{ON}=\frac{V_{0}-V_{S}}{L}T_{OFF}$, $V_{S}\left ( T_{ ON }+T_{关闭} \右)=V_{0}T_{关闭}$
$V_{0}=\frac{TV_{S}}{T_{OFF}}=\frac{V_{S}}{\frac{\left ( T+T_{ON} \right )}{T}} $
平均电压输出为:
$$V_{0}=\frac{V_{S}}{1-D}$$上式表明,V o可以在 V S到无穷大之间变化。它证明输出电压始终大于输入电压,因此它会升高或增加电压电平。
降压斩波器
这也称为降压转换器。在该斩波器中,平均电压输出V O小于输入电压V S。当斩波器打开时,V O = V S;当斩波器关闭时,V O = 0
当斩波器打开时 -
$V_{S}=\left ( V_{L}+V_{0} \right ),\quad V_{L}=V_{S}-V_{0},\quad L\frac{di}{dt} =V_{S}-V_{0},\quad L\frac{\Delta i}{T_{ON}}=V_{s}+V_{0}$
因此,峰峰值电流负载由下式给出:
$\Delta i=\frac{V_{s}-V_{0}}{L}T_{ON}$
电路原理图
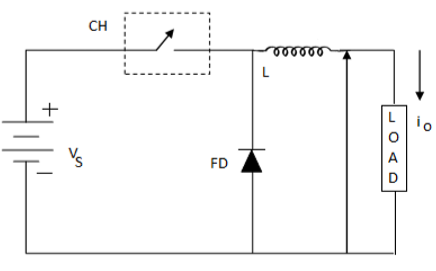
其中FD为续流二极管。
当斩波器关闭时,电感器会发生极性反转和放电。电流通过续流二极管和电感到达负载。这给出了,
$$L\frac{di}{dt}=V_{0}................................ ......\左(我\右)$$重写为 -$\quad L\frac{\Delta i}{T_{OFF}}=V_{0}$
$$\Delta i=V_{0}\frac{T_{OFF}}{L}........................ ......\左 ( ii \右 )$$将等式 (i) 和 (ii) 等式得出:
$\frac{V_{S}-V_{0}}{L}T_{ON}=\frac{V_{0}}{L}T_{OFF}$
$\frac{V_{S}-V_{0}}{V_{0}}=\frac{T_{OFF}}{T_{ON}}$
$\frac{V_{S}}{V_{0}}=\frac{T_{ON}-T_{OFF}}{T_{ON}}$
上式给出:
$$V_{0}=\frac{T_{ON}}{T}V_{S}=DV_{S}$$方程 (i) 给出 -
$\Delta i=\frac{V_{S}-DV_{S}}{L}DT$,来自 $D=\frac{T_{ON}}{T}$
$=\frac{V_{S}-\left ( 1-D \right )D}{Lf}$
$f=\frac{1}{T}=$斩波频率
电流和电压波形
电流和电压波形如下 -
对于降压斩波器,电压输出始终小于电压输入。下面的波形显示了这一点。
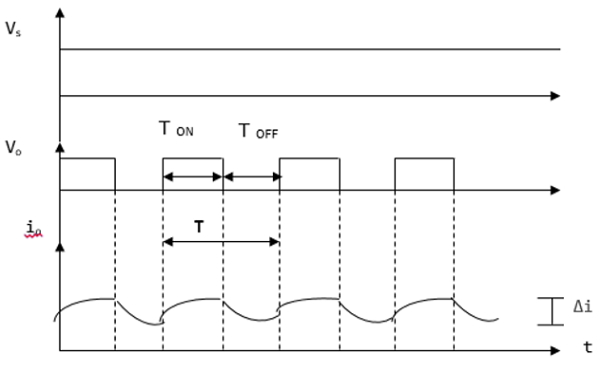
升压/降压斩波器
这也称为降压-升压转换器。它可以增加或减少电压输入电平。下图显示了降压-升压斩波器。
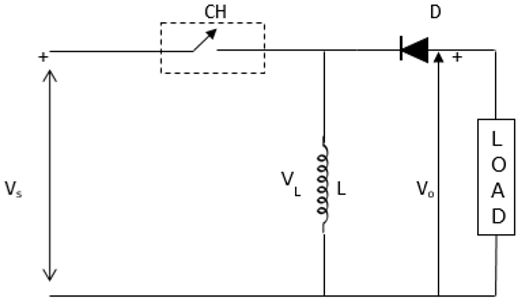
当斩波器接通时,电感器 L 被源电压 V s充电。因此,V s = V L。
$$L\frac{di}{dt}=V_{S}$$ $$\Delta i=\frac{V_{S}}{L}T_{ON}=\frac{V_{S}}{L }T\frac{T_{ON}}{T}=\frac{DV_{S}}{Lf}$$因为 -
$D=\frac{T_{ON}}{T}$ 和$f=\frac{1}{T} ........................ ......................\左 ( iii \右 )$
当斩波器关闭时,电感器的极性反转,这导致它通过二极管和负载放电。
因此,
$$V_{0}=-V_{L}$$ $$L\frac{di}{dt}=-V_{0}$$$L\frac{\Delta i}{T_{OFF}}=-V_{0}$,因此$\Delta i=-\frac{V_{0}}{L}T_{OFF}..... ......................\左 ( iv \右 )$
评估方程 (iii) 和 (iv) 得出 -
$\frac{DV_{S}}{Lf}=-\frac{V_{0}}{L}T_{关闭}$, $DV_{S}=-DV_{S}=-V_{0}T_{关}f$
$DV_{S}=-V_{0}\frac{T-T_{ON}}{T}=-V_{0}\left ( 1-\frac{T_{ON}}{T} \right )$ , $V_{0}=-\frac{DV_{S}}{1-D}$
因为$D=\frac{T_{ON}}{T}=\frac{T-T_{OFF}}{1-D}$
这给出了,
$V_{0}=\frac{DV_{S}}{1-D}$
D可以在0到1之间变化。当D=0时;VO = 0
当D = 0.5时,V O = V S
当D = 1时,V O = ∞。
因此,在 0 ≤ D ≤ 0.5 区间内,输出电压在 0 ≤ V O < V S范围内变化,我们得到降压或降压操作。而在 0.5 ≤ D ≤ 1 区间内,输出电压在 V S ≤ V O ≤ ∞范围内变化,我们得到升压或升压操作。
电力电子 - 控制方法
在转换器中,有两种基本控制方法用于改变输出电压。这些是 -
- 时间比例控制
- 限流控制
时间比例控制
在时间比率控制中,$\frac{T_{ON}}{T}$ 给出的常数 k 是变化的。常数k称为占空比。时间比率控制可以通过两种方式实现 -
恒定频率
在该控制方法中,频率(f=1/T 0N)保持恒定,而导通时间T变化。这称为脉冲宽度调制 (PWM)。
变频
在变频技术中,频率 (f = 1/T) 变化,而导通时间 T 保持恒定。这称为频率调制控制。
限流控制
在直流到直流转换器中,电流值在连续电压的最大和最小水平之间变化。在该技术中,斩波器(DC-DC 转换器中的开关)先打开再关闭,以确保电流在上限和下限之间保持恒定。当电流超过最大点时,斩波器关闭。
当开关处于关闭状态时,电流通过二极管续流并以指数方式下降。当电流达到最低水平时,斩波器打开。当导通时间 T 恒定或频率 (f=1/T) 时,都可以使用该方法。
电力电子 - 谐振开关
谐振开关变换器是指具有电感器和电容器(LC)网络并且在每个开关周期期间电流和电压波形以正弦方式变化的变换器。有各种谐振开关转换器 -
- 谐振直流到直流转换器
- 直流转交流逆变器
- 谐振交流逆变器至直流转换器
在本教程中,我们将重点关注谐振直流到直流转换器
谐振直流至直流转换器
下面使用 DC-DC 转换器解释开关模式电源 (SMPS) 的概念。为负载提供从主电源V IN获得的恒定电压电源(V OUT ) 。V OUT的值通过改变串联电阻 (R S ) 或并联连接的电流源 ( I S ) 来调节。通过改变I S来控制 V OUT并确保 R S保持恒定,转换器中会损失大量功率。

开关模式电源 (SMPS)
SMPS(开关模式电源)是指使用开关调节器以有效方式转换电力的电子设备。SMPS 从主电源线获取电力并将其传输到负载。例如,计算机同时保证电压和电流特性进行转换。
SMPS 和线性电源之间的区别在于,前者在低耗散期间保持打开和关闭,而在高耗散区域使用较少的时间。这确保了更少的能源浪费。实际上,SMPS 不会消耗任何功率。
与相同尺寸和形状的普通线性电源设备相比,SMPS 的尺寸更小且非常轻。

下图显示了 SMPS 的电路图。当开关频率改变时,每个周期存储的能量可以改变,因此电压输出也改变。

下面的波形适用于半桥转换器,也称为推挽式转换器。它用于利用高功率的应用。如波形所示,输入电压减半。

DC-DC 转换器解决示例
升压斩波器的输入电压为 150V。所需电压输出为450V。假设晶闸管的导通时间为150μs。计算斩波频率。
解决方案 -
斩波频率 (f)
$f=\frac{1}{T}$
其中T – 斩波时间段 = $T_{ON}+T_{OFF}$
给定 − $V_{S}=150V$ $V_{0}=450V$ $T_{ON}=150\mu sec$
$V_{0}=V_{S\left ( \frac{T}{T-T_{ON}} \right )}$
$450=150\frac{T}{T-150^{-6}}$ $T=225\mu 秒$
因此,$f=\frac{1}{225\ast 10^{-6}}=4.44KHz$
新的电压输出,条件是脉冲宽度减半后以恒定频率运行。
将脉冲宽度减半给出 -
$$T_{ON}=\frac{150\times 10^{-6}}{2}=75\mu sec$$因此频率是恒定的,
$$f=4.44KHz$$ $$T=\frac{1}{f}=150\mu sec$$电压输出由下式给出 -
$$V_{0}=V_{S}\left ( \frac{T}{T-T_{ON}} \right )=150\times \left ( \frac{150\times 10^{-6}} {\left ( 150-75 \right )\times 10^{-6}} \right )=300V$$电力电子 - 逆变器类型
逆变器是指将直流电能转换为所需频率和电压输出的交流电能的电力电子装置。
逆变器分为两大类 -
电压源逆变器(VSI) - 电压源逆变器具有刚性直流源电压,即直流电压在逆变器输入端子处具有有限阻抗或零阻抗。
电流源逆变器 (CSI) - 电流源逆变器由高阻抗直流源提供可变电流。产生的电流波不受负载的影响。
单相逆变器
单相逆变器有两种类型:全桥逆变器和半桥逆变器。
半桥逆变器
这种类型的逆变器是全桥逆变器的基本构建模块。它包含两个开关,每个电容器的电压输出等于 $\frac{V_{dc}}{2}$。此外,这些开关是互补的,也就是说,如果一个开关打开,另一个开关就会关闭。
全桥逆变器
该逆变器电路将直流电转换为交流电。它通过按正确的顺序关闭和打开开关来实现这一点。它有四种不同的操作状态,具体取决于哪些开关闭合。
三相逆变器
三相逆变器将直流输入转换为三相交流输出。其三个臂通常延迟120°的角度以产生三相交流电源。逆变器每次切换的比例为 50%,并且在时间 T(60° 角度间隔)的每 T/6 后发生切换。开关S1和S4、开关S2和S5以及开关S3和S6彼此互补。
下图显示了三相逆变器的电路。它只不过是将三个单相逆变器置于同一直流电源上。三相逆变器中的极电压等于单相半桥逆变器中的极电压。

上述两种类型的逆变器有两种导通模式——180°导通模式和120°导通模式。
180° 传导模式
在这种导通模式下,每个器件都处于 180° 的导通状态,并且以 60° 的间隔打开。端子A、B、C是电桥的输出端子,连接负载的三相三角形或星形连接。
下图解释了平衡星形连接负载的操作。在 0° – 60° 期间,点 S1、S5 和 S6 处于导通模式。负载的端子 A 和 C 连接到电源的正极点。端子 B 在其负点连接至源极。另外,电阻R/2位于中性端和正极端子之间,电阻R位于中性端和负极端子之间。

|
负载电压如下; VAN = V/3, V BN = −2V/3, 电压CN =V/3 |
线电压如下; V AB = V AN – V BN = V, VBC = VBN - VCN =-V , VCA = VCN - VAN = 0 |
180° 传导模式的波形

120° 传导模式
在这种导通模式下,每个电子器件都处于120°的导通状态。它最适合负载中的三角形连接,因为它会在任何相位上产生六步类型的波形。因此,在任何时刻只有两个器件导通,因为每个器件仅以 120° 导通。
负载上的端子 A 连接到电源的正极,端子 B 连接到电源的负极。负载上的端子C处于悬浮状态。此外,相电压等于负载电压,如下所示。
相电压 = 线电压
V AB = V
VBC = -V/2
V CA = −V/2
120° 传导模式的波形

电力电子 - 脉宽调制
PWM 是一种用于降低负载电流中的总谐波失真 (THD) 的技术。它使用矩形/正方形形式的脉冲波,在调制其脉冲宽度后产生可变的平均波形值 f(t)。调制的时间周期由 T 给出。因此,波形平均值由下式给出
$$\bar{y}=\frac{1}{T}\int_{0}^{T}f\left ( t \right )dt$$
正弦脉宽调制
在简单的源电压逆变器中,开关可以根据需要打开和关闭。在每个周期内,开关打开或关闭一次。这会产生方波。然而,如果多次接通开关,则获得改善波形的谐波分布。
通过将所需的调制波形与高频三角波进行比较,获得正弦 PWM 波形。无论信号电压比载波电压小还是大,直流母线的输出电压要么为负,要么为正。

正弦振幅被给定为 A m,载体三角形的振幅被给定为 A c。对于正弦 PWM,调制指数 m 由 A m /A c给出。
修正正弦波形 PWM
改进的正弦 PWM 波形用于功率控制和功率因数优化。主要概念是通过修改 PWM 转换器将电网上延迟的电流转移到电压电网。因此,电源效率得到提高,功率因数得到优化。

多重脉宽调制
多重 PWM 具有许多输出,这些输出的值不相同,但产生这些输出的时间周期对于所有输出来说都是恒定的。具有 PWM 的逆变器能够在高电压输出下运行。

下面的波形是由多个 PWM 产生的正弦波

电压与谐波控制
具有频率(频率为 60Hz 的基波功率的多重积分)的周期波形称为谐波。另一方面,总谐波失真 (THD) 是指所有谐波电流频率的总贡献。
谐波的特征在于脉冲,该脉冲代表给定电路中使用的整流器的数量。计算如下 -
$$h=\left ( n\times P \right )+1 \quad 或 \quad -1$$其中n − 是整数 1, 2, 3, 4….n
P - 整流器数量
总结如下表 -
谐波 |
频率 |
| 第一名 | 60赫兹 |
| 第二次 | 120赫兹 |
| 第三名_ | 180赫兹 |
| 4号 | 240赫兹 |
|
第五名 。 。 49号 |
300赫兹 。 。 |