AI 与 Python – 机器学习

学习是指通过学习或经验获得知识或技能。基于此，我们可以将机器学习（ML）定义如下 -

它可以被定义为计算机科学领域，更具体地说是人工智能的应用，它为计算机系统提供了利用数据学习并从经验中改进的能力，而无需明确编程。

基本上，机器学习的主要焦点是让计算机自动学习而无需人工干预。现在的问题是如何开始和完成这样的学习？可以从数据观察开始。数据也可以是一些例子、指导或一些直接经验。然后，根据此输入，机器通过寻找数据中的某些模式来做出更好的决策。

机器学习 (ML) 的类型

机器学习算法可以帮助计算机系统无需显式编程即可学习。这些算法分为监督算法和无监督算法。现在让我们看一些算法 -

监督机器学习算法

这是最常用的机器学习算法。之所以称为监督式，是因为算法从训练数据集学习的过程可以被视为监督学习过程的老师。在这种机器学习算法中，可能的结果是已知的，并且训练数据也标有正确答案。可以理解如下 -

假设我们有输入变量x和输出变量y，并且我们应用算法来学习从输入到输出的映射函数，例如 -

Y = f(x)

现在，主要目标是很好地近似映射函数，以便当我们有新的输入数据 (x) 时，我们可以预测该数据的输出变量 (Y)。

主要监督学习问题可以分为以下两类问题 -

分类- 当我们有“黑色”、“教学”、“非教学”等分类输出时，问题称为分类问题。
回归- 当我们有实际值输出（例如“距离”、“千克”等）时，问题称为回归问题。

决策树、随机森林、knn、逻辑回归是监督机器学习算法的例子。

无监督机器学习算法

顾名思义，这类机器学习算法没有任何监督者提供任何形式的指导。这就是为什么无监督机器学习算法与一些人所说的真正的人工智能密切相关。可以理解如下 -

假设我们有输入变量 x，那么就不会像监督学习算法那样有相应的输出变量。

简单来说，我们可以说，在无监督学习中，不会有正确答案，也不会有老师指导。算法有助于发现数据中有趣的模式。

无监督学习问题可以分为以下两类问题 -

聚类- 在聚类问题中，我们需要发现数据中固有的分组。例如，根据客户的购买Behave对客户进行分组。
关联- 问题称为关联问题，因为此类问题需要发现描述大部分数据的规则。例如，查找同时购买x和y的客户。

用于聚类的 K 均值、用于关联的 Apriori 算法是无监督机器学习算法的示例。

强化机器学习算法

这类机器学习算法的使用非常少。这些算法训练系统做出具体决策。基本上，机器暴露在一个使用试错法不断自我训练的环境中。这些算法从过去的经验中学习，并尝试捕获最佳的知识以做出准确的决策。马尔可夫决策过程是强化机器学习算法的一个例子。

最常见的机器学习算法

在本节中，我们将了解最常见的机器学习算法。算法描述如下 -

线性回归

它是统计学和机器学习领域最著名的算法之一。

基本概念 - 主要线性回归是一种线性模型，假设输入变量 x 和单个输出变量 y 之间存在线性关系。换句话说，我们可以说 y 可以通过输入变量 x 的线性组合来计算。变量之间的关系可以通过拟合最佳线来建立。

线性回归的类型

线性回归有以下两种类型 -

简单线性回归- 如果线性回归算法只有一个自变量，则称为简单线性回归。
多元线性回归- 如果线性回归算法具有多个自变量，则称为多元线性回归。

线性回归主要用于基于连续变量估计真实值。例如，基于实际值，可以通过线性回归来估计商店一天的总销售额。

逻辑回归

它是一种分类算法，也称为Logit回归。

逻辑回归主要是一种分类算法，用于根据给定的一组自变量来估计离散值，如 0 或 1、真或假、是或否。基本上，它预测概率，因此其输出介于 0 和 1 之间。

决策树

决策树是一种监督学习算法，主要用于分类问题。

基本上它是一个分类器，表示为基于自变量的递归划分。决策树具有形成有根树的节点。有根树是一种有向树，其节点称为“根”。根节点没有任何传入边，所有其他节点都有一个传入边。这些节点称为叶子节点或决策节点。例如，考虑以下决策树来查看一个人是否适合。

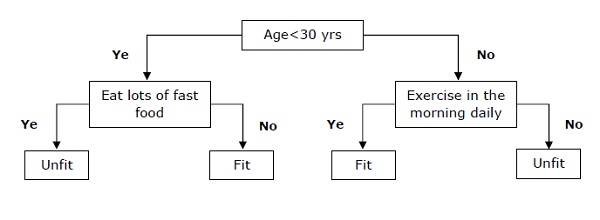
支持向量机（SVM）

它用于分类和回归问题。但主要用于分类问题。SVM的主要概念是将每个数据项绘制为n维空间中的一个点，每个特征的值是特定坐标的值。这里 n 是我们将拥有的特征。以下是理解 SVM 概念的简单图形表示 -

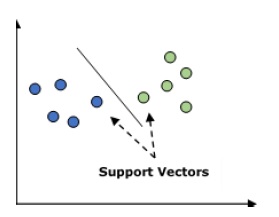
在上图中，我们有两个特征，因此我们首先需要在二维空间中绘制这两个变量，其中每个点都有两个坐标，称为支持向量。该线将数据分为两个不同的分类组。这条线就是分类器。

朴素贝叶斯

这也是一种分类技术。这种分类技术背后的逻辑是使用贝叶斯定理来构建分类器。假设预测变量是独立的。简而言之，它假设类中特定功能的存在与任何其他功能的存在无关。以下是贝叶斯定理的方程 -

$$P\left ( \frac{A}{B} \right ) = \frac{P\left ( \frac{B}{A} \right )P\left ( A \right )}{P\left ( B \右）}$$

朴素贝叶斯模型易于构建，对于大型数据集特别有用。

K 最近邻 (KNN)

它用于问题的分类和回归。它被广泛用于解决分类问题。该算法的主要概念是它用于存储所有可用的案例，并通过其 k 个邻居的多数票对新案例进行分类。然后将该案例分配给通过距离函数测量的 K 最近邻中最常见的类。距离函数可以是欧氏距离、闵可夫斯基距离和汉明距离。使用 KNN 时请考虑以下因素 -

KNN 的计算成本比用于分类问题的其他算法昂贵。
需要对变量进行标准化，否则较高范围的变量可能会产生偏差。
在KNN中，我们需要进行预处理阶段，例如噪声去除。

K 均值聚类

顾名思义，它是用来解决聚类问题的。它基本上是一种无监督学习。K-Means聚类算法的主要逻辑是通过多个聚类对数据集进行分类。按照以下步骤通过 K-means 形成簇 -

K 均值为每个簇选取 k 个点（称为质心）。
现在每个数据点形成一个具有最近质心的簇，即k个簇。
现在，它将根据现有的集群成员找到每个集群的质心。
我们需要重复这些步骤直到收敛。

随机森林

它是一种监督分类算法。随机森林算法的优点是它可以用于分类和回归类型的问题。基本上它是决策树（即森林）的集合，或者你可以说决策树的集合。随机森林的基本概念是每棵树给出一个分类，森林从中选择最好的分类。以下是随机森林算法的优点 -

随机森林分类器可用于分类和回归任务。
他们可以处理缺失值。
即使森林中有更多的树木，它也不会过度拟合模型。