AI with Python – 监督学习：分类

在本章中，我们将重点关注监督学习的实现——分类。

分类技术或模型试图从观察值中得出一些结论。在分类问题中，我们有分类输出，例如“黑色”或“白色”或“教学”和“非教学”。在构建分类模型时，我们需要包含数据点和相应标签的训练数据集。例如，如果我们想检查图像是否是汽车。为了检查这一点，我们将构建一个训练数据集，其中包含与“汽车”和“无汽车”相关的两个类别。然后我们需要使用训练样本来训练模型。分类模型主要应用于人脸识别、垃圾邮件识别等。

在 Python 中构建分类器的步骤

为了用 Python 构建分类器，我们将使用 Python 3 和 Scikit-learn（一种机器学习工具）。按照以下步骤在 Python 中构建分类器 -

第 1 步 - 导入 Scikit-learn

这将是用 Python 构建分类器的第一步。在此步骤中，我们将安装一个名为 Scikit-learn 的 Python 包，它是 Python 中最好的机器学习模块之一。以下命令将帮助我们导入包 -

Import Sklearn

步骤 2 - 导入 Scikit-learn 的数据集

在此步骤中，我们可以开始使用机器学习模型的数据集。在这里，我们将使用威斯康星州乳腺癌诊断数据库。该数据集包括有关乳腺癌肿瘤的各种信息，以及恶性或良性的分类标签。该数据集包含 569 个肿瘤的 569 个实例或数据，包括 30 个属性或特征的信息，例如肿瘤的半径、纹理、平滑度和面积。借助以下命令，我们可以导入 Scikit-learn 的乳腺癌数据集 -

from sklearn.datasets import load_breast_cancer

现在，以下命令将加载数据集。

data = load_breast_cancer()

以下是重要字典键的列表 -

  • 分类标签名称(target_names)
  • 实际标签（目标）
  • 属性/特征名称(feature_names)
  • 属性（数据）

现在，借助以下命令，我们可以为每组重要的信息创建新变量并分配数据。换句话说，我们可以使用以下命令组织数据 -

label_names = data['target_names']
labels = data['target']
feature_names = data['feature_names']
features = data['data']

现在，为了更清楚，我们可以借助以下命令打印类标签、第一个数据实例的标签、特征名称和特征值 -

print(label_names)

上面的命令将分别打印恶性和良性的类名称。其输出如下所示 -

['malignant' 'benign']

现在，下面的命令将显示它们映射到二进制值 0 和 1。这里 0 代表恶性癌症，1 代表良性癌症。您将收到以下输出 -

print(labels[0])
0

下面给出的两个命令将生成特征名称和特征值。

print(feature_names[0])
mean radius
print(features[0])
[ 1.79900000e+01 1.03800000e+01 1.22800000e+02 1.00100000e+03
  1.18400000e-01 2.77600000e-01 3.00100000e-01 1.47100000e-01
  2.41900000e-01 7.87100000e-02 1.09500000e+00 9.05300000e-01
  8.58900000e+00 1.53400000e+02 6.39900000e-03 4.90400000e-02
  5.37300000e-02 1.58700000e-02 3.00300000e-02 6.19300000e-03
  2.53800000e+01 1.73300000e+01 1.84600000e+02 2.01900000e+03
  1.62200000e-01 6.65600000e-01 7.11900000e-01 2.65400000e-01
  4.60100000e-01 1.18900000e-01]

从上面的输出中，我们可以看到第一个数据实例是一个半径为1.7990000e+01的恶性肿瘤。

步骤 3 - 将数据组织成集合

在这一步中，我们将把数据分为两部分，即训练集和测试集。将数据分成这些组非常重要，因为我们必须在看不见的数据上测试我们的模型。为了将数据分成集合，sklearn 有一个名为train_test_split()函数的函数。借助以下命令，我们可以分割这些集合中的数据 -

from sklearn.model_selection import train_test_split

上面的命令将从 sklearn 导入train_test_split函数，下面的命令将数据拆分为训练数据和测试数据。在下面给出的示例中，我们使用 40% 的数据进行测试，其余数据将用于训练模型。

train, test, train_labels, test_labels = train_test_split(features,labels,test_size = 0.40, random_state = 42)

第 4 步 - 构建模型

在这一步中，我们将构建我们的模型。我们将使用朴素贝叶斯算法来构建模型。以下命令可用于构建模型 -

from sklearn.naive_bayes import GaussianNB

上面的命令将导入 GaussianNB 模块。现在，以下命令将帮助您初始化模型。

gnb = GaussianNB()

我们将使用 gnb.fit() 将模型拟合到数据来训练模型。

model = gnb.fit(train, train_labels)

步骤 5 - 评估模型及其准确性

在此步骤中，我们将通过对测试数据进行预测来评估模型。然后我们也会发现它的准确性。为了进行预测，我们将使用 Predict() 函数。以下命令将帮助您执行此操作 -

preds = gnb.predict(test)
print(preds)

[1 0 0 1 1 0 0 0 1 1 1 0 1 0 1 0 1 1 1 0 1 1 0 1 1 1 1 1 1
 0 1 1 1 1 1 1 0 1 0 1 1 0 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 0 
 0 1 1 0 0 1 1 1 0 0 1 1 0 0 1 0 1 1 1 1 1 1 0 1 1 0 0 0 0 
 0 1 1 1 1 1 1 1 1 0 0 1 0 0 1 0 0 1 1 1 0 1 1 0 1 1 0 0 0 
 1 1 1 0 0 1 1 0 1 0 0 1 1 0 0 0 1 1 1 0 1 1 0 0 1 0 1 1 0 
 1 0 0 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 0 
 1 1 0 1 1 1 1 1 1 0 0 0 1 1 0 1 0 1 1 1 1 0 1 1 0 1 1 1 0 
 1 0 0 1 1 1 1 1 1 1 1 0 1 1 1 1 1 0 1 0 0 1 1 0 1]

上述 0 和 1 系列是肿瘤类别（恶性和良性）的预测值。

现在，通过比较两个数组，即test_labels和preds，我们可以找出模型的准确性。我们将使用precision_score()函数来确定准确性。为此考虑以下命令 -

from sklearn.metrics import accuracy_score
print(accuracy_score(test_labels,preds))
0.951754385965

结果表明，NaïveBayes 分类器的准确率为 95.17%。

这样，借助上述步骤，我们就可以用 Python 构建我们的分类器了。

用 Python 构建分类器

在本节中，我们将学习如何用 Python 构建分类器。

朴素贝叶斯分类器

朴素贝叶斯是一种分类技术，用于使用贝叶斯定理构建分类器。假设预测变量是独立的。简而言之，它假设类中特定功能的存在与任何其他功能的存在无关。为了构建朴素贝叶斯分类器，我们需要使用名为 scikit learn 的 python 库。scikit learn 包下有三种类型的朴素贝叶斯模型：高斯模型、多项式模型和伯努利模型。

要构建朴素贝叶斯机器学习分类器模型，我们需要以下 &minus

数据集

我们将使用名为威斯康星州乳腺癌诊断数据库的数据集。该数据集包括有关乳腺癌肿瘤的各种信息，以及恶性或良性的分类标签。该数据集包含 569 个肿瘤的 569 个实例或数据，包括 30 个属性或特征的信息，例如肿瘤的半径、纹理、平滑度和面积。我们可以从 sklearn 包导入这个数据集。

朴素贝叶斯模型

为了构建朴素贝叶斯分类器，我们需要一个朴素贝叶斯模型。如前所述，scikit learn 包下有三种类型的朴素贝叶斯模型，分别为高斯模型、多项式模型和伯努利模型。在下面的示例中，我们将使用高斯朴素贝叶斯模型。

通过以上内容，我们将建立一个朴素贝叶斯机器学习模型，利用肿瘤信息来预测肿瘤是恶性还是良性。

首先，我们需要安装 sklearn 模块。可以借助以下命令来完成 -

Import Sklearn

现在，我们需要导入名为“乳腺癌威斯康星州诊断数据库”的数据集。

from sklearn.datasets import load_breast_cancer

现在，以下命令将加载数据集。

data = load_breast_cancer()

数据可以组织如下 -

label_names = data['target_names']
labels = data['target']
feature_names = data['feature_names']
features = data['data']

现在，为了更清楚，我们可以借助以下命令打印类标签、第一个数据实例的标签、特征名称和特征值 -

print(label_names)

上面的命令将分别打印恶性和良性的类名称。其输出如下所示 -

['malignant' 'benign']

现在，下面给出的命令将显示它们映射到二进制值 0 和 1。这里 0 代表恶性癌症，1 代表良性癌症。其输出如下所示 -

print(labels[0])
0

以下两个命令将生成特征名称和特征值。

print(feature_names[0])
mean radius
print(features[0])

[ 1.79900000e+01 1.03800000e+01 1.22800000e+02 1.00100000e+03
  1.18400000e-01 2.77600000e-01 3.00100000e-01 1.47100000e-01
  2.41900000e-01 7.87100000e-02 1.09500000e+00 9.05300000e-01
  8.58900000e+00 1.53400000e+02 6.39900000e-03 4.90400000e-02
  5.37300000e-02 1.58700000e-02 3.00300000e-02 6.19300000e-03
  2.53800000e+01 1.73300000e+01 1.84600000e+02 2.01900000e+03
  1.62200000e-01 6.65600000e-01 7.11900000e-01 2.65400000e-01
  4.60100000e-01 1.18900000e-01]

从上面的输出中，我们可以看到第一个数据实例是一个恶性肿瘤，其主半径为1.7990000e+01。

为了在看不见的数据上测试我们的模型，我们需要将数据分为训练数据和测试数据。可以借助以下代码来完成 -

from sklearn.model_selection import train_test_split

上面的命令将从 sklearn 导入train_test_split函数，下面的命令将数据拆分为训练数据和测试数据。在下面的示例中，我们使用 40% 的数据进行测试，重新挖掘的数据将用于训练模型。

train, test, train_labels, test_labels = 
train_test_split(features,labels,test_size = 0.40, random_state = 42)

现在，我们使用以下命令构建模型 -

from sklearn.naive_bayes import GaussianNB

上面的命令将导入GaussianNB模块。现在，使用下面给出的命令，我们需要初始化模型。

gnb = GaussianNB()

我们将使用gnb.fit()将模型拟合到数据来训练模型。

model = gnb.fit(train, train_labels)

现在，通过对测试数据进行预测来评估模型，可以按如下方式完成 -

preds = gnb.predict(test)
print(preds)

[1 0 0 1 1 0 0 0 1 1 1 0 1 0 1 0 1 1 1 0 1 1 0 1 1 1 1 1 1
 0 1 1 1 1 1 1 0 1 0 1 1 0 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 0 
 0 1 1 0 0 1 1 1 0 0 1 1 0 0 1 0 1 1 1 1 1 1 0 1 1 0 0 0 0 
 0 1 1 1 1 1 1 1 1 0 0 1 0 0 1 0 0 1 1 1 0 1 1 0 1 1 0 0 0 
 1 1 1 0 0 1 1 0 1 0 0 1 1 0 0 0 1 1 1 0 1 1 0 0 1 0 1 1 0 
 1 0 0 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 0 
 1 1 0 1 1 1 1 1 1 0 0 0 1 1 0 1 0 1 1 1 1 0 1 1 0 1 1 1 0 
 1 0 0 1 1 1 1 1 1 1 1 0 1 1 1 1 1 0 1 0 0 1 1 0 1]

上述 0 和 1 系列是肿瘤类别（即恶性和良性）的预测值。

现在，通过比较两个数组，即test_labels和preds，我们可以找出模型的准确性。我们将使用precision_score()函数来确定准确性。考虑以下命令 -

from sklearn.metrics import accuracy_score
print(accuracy_score(test_labels,preds))
0.951754385965

结果表明 NaïveBayes 分类器的准确率为 95.17%。

那是基于朴素贝叶斯高斯模型的机器学习分类器。

支持向量机 (SVM)

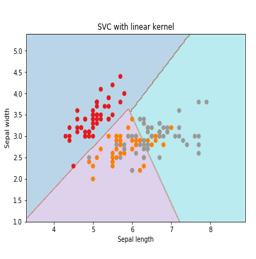
基本上，支持向量机（SVM）是一种监督机器学习算法，可用于回归和分类。SVM的主要概念是将每个数据项绘制为n维空间中的一个点，每个特征的值是特定坐标的值。这里 n 是我们将拥有的特征。以下是理解 SVM 概念的简单图形表示 -

支持向量机2

在上图中，我们有两个特征。因此，我们首先需要在二维空间中绘制这两个变量，其中每个点都有两个坐标，称为支持向量。该线将数据分为两个不同的分类组。这条线就是分类器。

在这里，我们将使用 scikit-learn 和 iris 数据集构建一个 SVM 分类器。Scikitlearn 库具有sklearn.svm模块，并提供 sklearn.svm.svc 进行分类。基于 4 个特征预测鸢尾植物类别的 SVM 分类器如下所示。

数据集

我们将使用鸢尾花数据集，该数据集包含 3 个类别，每个类别 50 个实例，其中每个类别指一种鸢尾植物。每个实例都有四个特征，即萼片长度、萼片宽度、花瓣长度和花瓣宽度。基于 4 个特征预测鸢尾植物类别的 SVM 分类器如下所示。

核心

这是SVM使用的一种技术。基本上，这些函数采用低维输入空间并将其转换为高维空间。它将不可分离的问题转化为可分离的问题。核函数可以是线性、多项式、rbf和sigmoid中的任意一种。在此示例中，我们将使用线性内核。

现在让我们导入以下包 -

import pandas as pd
import numpy as np
from sklearn import svm, datasets
import matplotlib.pyplot as plt

现在，加载输入数据 -

iris = datasets.load_iris()

我们采用前两个特征 -

X = iris.data[:, :2]
y = iris.target

我们将用原始数据绘制支持向量机边界。我们正在创建一个网格来绘制。

x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
h = (x_max / x_min)/100
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
X_plot = np.c_[xx.ravel(), yy.ravel()]

我们需要给出正则化参数的值。

C = 1.0

我们需要创建 SVM 分类器对象。

Svc_classifier = svm_classifier.SVC(kernel='linear', 
C=C, decision_function_shape = 'ovr').fit(X, y)
Z = svc_classifier.predict(X_plot)
Z = Z.reshape(xx.shape)
plt.figure(figsize = (15, 5))
plt.subplot(121)
plt.contourf(xx, yy, Z, cmap = plt.cm.tab10, alpha = 0.3)
plt.scatter(X[:, 0], X[:, 1], c = y, cmap = plt.cm.Set1)
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.xlim(xx.min(), xx.max())
plt.title('SVC with linear kernel')
带衬垫内核的 svc

逻辑回归

基本上，逻辑回归模型是监督分类算法家族的成员之一。逻辑回归通过使用逻辑函数估计概率来衡量因变量和自变量之间的关系。

在这里，如果我们谈论因变量和自变量，那么因变量就是我们要预测的目标类变量，而自变量则是我们要用来预测目标类的特征。

在逻辑回归中，估计概率意味着预测事件发生的可能性。例如，店主想要预测进入商店的顾客是否会购买游戏机（例如）。店主会观察顾客的许多特征——性别、年龄等，以预测发生的可能性，即是否购买游戏机。逻辑函数是 S 形曲线，用于构建具有各种参数的函数。

先决条件

在使用逻辑回归构建分类器之前，我们需要在系统上安装 Tkinter 包。它可以从https://docs.python.org/2/library/tkinter.html安装。

现在，借助下面给出的代码，我们可以使用逻辑回归创建一个分类器 -

首先，我们将导入一些包 -

import numpy as np
from sklearn import linear_model
import matplotlib.pyplot as plt

现在，我们需要定义样本数据，可以按如下方式完成 -

X = np.array([[2, 4.8], [2.9, 4.7], [2.5, 5], [3.2, 5.5], [6, 5], [7.6, 4],
              [3.2, 0.9], [2.9, 1.9],[2.4, 3.5], [0.5, 3.4], [1, 4], [0.9, 5.9]])
y = np.array([0, 0, 0, 1, 1, 1, 2, 2, 2, 3, 3, 3])

接下来，我们需要创建逻辑回归分类器，可以按如下方式完成 -

Classifier_LR = linear_model.LogisticRegression(solver = 'liblinear', C = 75)

最后但并非最不重要的一点是，我们需要训练这个分类器 -

Classifier_LR.fit(X, y)

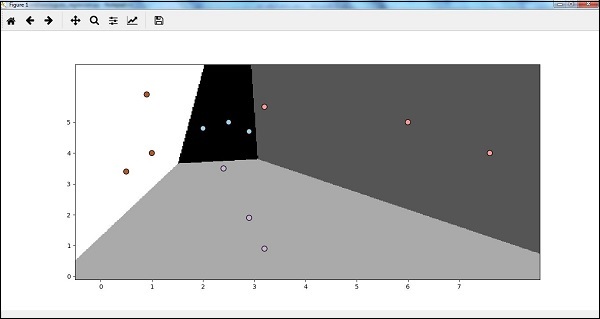
现在，我们如何可视化输出？可以通过创建一个名为 Logistic_visualize() 的函数来完成 -

Def Logistic_visualize(Classifier_LR, X, y):
   min_x, max_x = X[:, 0].min() - 1.0, X[:, 0].max() + 1.0
   min_y, max_y = X[:, 1].min() - 1.0, X[:, 1].max() + 1.0

在上面的行中，我们定义了网格中使用的最小和最大值 X 和 Y。此外，我们将定义绘制网格的步长。

mesh_step_size = 0.02

让我们定义 X 和 Y 值的网格如下 -

x_vals, y_vals = np.meshgrid(np.arange(min_x, max_x, mesh_step_size),
                 np.arange(min_y, max_y, mesh_step_size))

借助以下代码，我们可以在网格上运行分类器 -

output = classifier.predict(np.c_[x_vals.ravel(), y_vals.ravel()])
output = output.reshape(x_vals.shape)
plt.figure()
plt.pcolormesh(x_vals, y_vals, output, cmap = plt.cm.gray)
 
plt.scatter(X[:, 0], X[:, 1], c = y, s = 75, edgecolors = 'black', 
linewidth=1, cmap = plt.cm.Paired)

以下代码行将指定绘图的边界

plt.xlim(x_vals.min(), x_vals.max())
plt.ylim(y_vals.min(), y_vals.max())
plt.xticks((np.arange(int(X[:, 0].min() - 1), int(X[:, 0].max() + 1), 1.0)))
plt.yticks((np.arange(int(X[:, 1].min() - 1), int(X[:, 1].max() + 1), 1.0)))
plt.show()

现在，运行代码后我们将得到以下输出，逻辑回归分类器 -

逻辑回归

决策树分类器

决策树基本上是一个二叉树流程图，其中每个节点根据某些特征变量分割一组观察值。

在这里，我们正在构建一个决策树分类器来预测男性或女性。我们将采用一个非常小的数据集，包含 19 个样本。这些样本将包含两个特征——“身高”和“头发长度”。

先决条件

为了构建以下分类器，我们需要安装pydotplus和graphviz。基本上，graphviz 是一个使用点文件绘制图形的工具，而pydotplus是 Graphviz 的 Dot 语言的模块。可以使用包管理器或 pip 安装。

现在，我们可以借助以下 Python 代码构建决策树分类器 -

首先，让我们导入一些重要的库，如下所示 -

import pydotplus
from sklearn import tree
from sklearn.datasets import load_iris
from sklearn.metrics import classification_report
from sklearn import cross_validation
import collections

现在，我们需要提供数据集，如下所示 -

X = [[165,19],[175,32],[136,35],[174,65],[141,28],[176,15],[131,32],
[166,6],[128,32],[179,10],[136,34],[186,2],[126,25],[176,28],[112,38],
[169,9],[171,36],[116,25],[196,25]]

Y = ['Man','Woman','Woman','Man','Woman','Man','Woman','Man','Woman',
'Man','Woman','Man','Woman','Woman','Woman','Man','Woman','Woman','Man']
data_feature_names = ['height','length of hair']

X_train, X_test, Y_train, Y_test = cross_validation.train_test_split
(X, Y, test_size=0.40, random_state=5)

提供数据集后，我们需要拟合模型，可以按如下方式完成 -

clf = tree.DecisionTreeClassifier()
clf = clf.fit(X,Y)

可以借助以下 Python 代码进行预测 -

prediction = clf.predict([[133,37]])
print(prediction)

我们可以借助以下 Python 代码可视化决策树 -

dot_data = tree.export_graphviz(clf,feature_names = data_feature_names,
            out_file = None,filled = True,rounded = True)
graph = pydotplus.graph_from_dot_data(dot_data)
colors = ('orange', 'yellow')
edges = collections.defaultdict(list)

for edge in graph.get_edge_list():
edges[edge.get_source()].append(int(edge.get_destination()))

for edge in edges: edges[edge].sort()

for i in range(2):dest = graph.get_node(str(edges[edge][i]))[0]
dest.set_fillcolor(colors[i])
graph.write_png('Decisiontree16.png')

它将上述代码的预测为['Woman']并创建以下决策树 -

决策树

我们可以改变预测中的特征值来测试它。

随机森林分类器

众所周知，集成方法是将机器学习模型组合成更强大的机器学习模型的方法。随机森林（决策树的集合）就是其中之一。它比单个决策树更好，因为在保留预测能力的同时，它可以通过平均结果来减少过度拟合。在这里，我们将在 scikit learn 癌症数据集上实现随机森林模型。

导入必要的包 -

from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
import matplotlib.pyplot as plt
import numpy as np

现在，我们需要提供数据集，可以按如下方式完成&minus

cancer = load_breast_cancer()
X_train, X_test, y_train,
y_test = train_test_split(cancer.data, cancer.target, random_state = 0)

提供数据集后，我们需要拟合模型，可以按如下方式完成 -

forest = RandomForestClassifier(n_estimators = 50, random_state = 0)
forest.fit(X_train,y_train)

现在，获得训练和测试子集的准确性：如果我们增加估计器的数量，测试子集的准确性也会增加。

print('Accuracy on the training subset:(:.3f)',format(forest.score(X_train,y_train)))
print('Accuracy on the training subset:(:.3f)',format(forest.score(X_test,y_test)))

输出

Accuracy on the training subset:(:.3f) 1.0
Accuracy on the training subset:(:.3f) 0.965034965034965

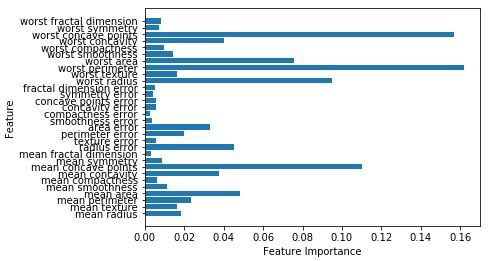
现在，与决策树一样，随机森林具有feature_importance模块，它将提供比决策树更好的特征权重视图。它可以绘制和可视化如下 -

n_features = cancer.data.shape[1]
plt.barh(range(n_features),forest.feature_importances_, align='center')
plt.yticks(np.arange(n_features),cancer.feature_names)
plt.xlabel('Feature Importance')
plt.ylabel('Feature')
plt.show()
特征重要性

分类器的性能

实现机器学习算法后，我们需要了解模型的有效性。用于测量有效性的标准可以基于数据集和度量。为了评估不同的机器学习算法，我们可以使用不同的性能指标。例如，假设如果使用分类器来区分不同对象的图像，我们可以使用平均准确度、AUC 等分类性能指标。从某种意义上说，我们选择评估机器学习模型的指标是非常重要，因为指标的选择会影响机器学习算法性能的测量和比较方式。以下是一些指标 -

混淆矩阵

基本上它用于分类问题，其中输出可以是两种或多种类型的类。这是衡量分类器性能的最简单方法。混淆矩阵基本上是一个具有两个维度的表格，即“实际”和“预测”。两个维度都有“True Positives (TP)”、“True Negatives (TN)”、“False Positives (FP)”、“False Negatives (FN)”。

混淆矩阵

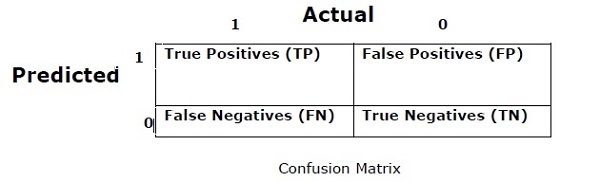
在上面的混淆矩阵中，1 代表正类，0 代表负类。

以下是与混淆矩阵相关的术语 -

  • True Positives - TP 是数据点的实际类别为 1 并且预测也是 1 的情况。

  • True Negatives - TN 是数据点的实际类别为 0 并且预测也为 0 的情况。

  • 误报 - FP 是数据点的实际类别为 0 而预测也为 1 的情况。

  • 假阴性 - FN 是数据点的实际类别为 1 而预测也为 0 的情况。

准确性

混淆矩阵本身并不是性能度量，但几乎所有性能矩阵都基于混淆矩阵。其中之一是准确性。在分类问题中，它可以定义为模型在所有类型的预测中做出的正确预测的数量。计算精度的公式如下 -

$$准确度 = \frac{TP+TN}{TP+FP+FN+TN}$$

精确

它主要用于文档检索。它可以被定义为有多少返回的文档是正确的。以下是计算精度的公式 -

$$精度 = \frac{TP}{TP+FP}$$

召回率或灵敏度

它可以定义为模型返回多少正值。以下是计算模型召回率/灵敏度的公式 -

$$回忆 = \frac{TP}{TP+FN}$$

特异性

它可以定义为模型返回多少负数。这与回忆正好相反。以下是计算模型特异性的公式 -

$$特异性 = \frac{TN}{TN+FP}$$

类别不平衡问题

类别不平衡是指属于一个类别的观察数量明显低于属于其他类别的观察数量的情况。例如，在需要识别罕见病、银行欺诈交易等场景下，这个问题就很突出。

不平衡类别的示例

让我们考虑一个欺诈检测数据集的例子来理解不平衡类的概念 -

Total observations = 5000
Fraudulent Observations = 50
Non-Fraudulent Observations = 4950
Event Rate = 1%

解决方案

平衡阶级的Behave是阶级不平衡的解决方案。平衡类别的主要目标是增加少数类别的频率或减少多数类别的频率。以下是解决不平衡类别问题的方法 -

重新采样

重采样是用于重建样本数据集（训练集和测试集）的一系列方法。进行重采样以提高模型的准确性。以下是一些重采样技术 -

  • 随机欠采样- 该技术旨在通过随机消除多数类示例来平衡类分布。这样做直到多数类实例和少数类实例达到平衡为止。

Total observations = 5000
Fraudulent Observations = 50
Non-Fraudulent Observations = 4950
Event Rate = 1%

在这种情况下，我们从非欺诈实例中抽取 10% 的样本而不进行替换，然后将它们与欺诈实例结合起来 -

随机抽样后的非欺诈性观察 = 4950 的 10% = 495

与欺诈性观察结果相结合后的观察总数 = 50+495 = 545

因此，现在，采样不足后新数据集的事件率 = 9%

该技术的主要优点是可以减少运行时间并改进存储。但另一方面，它会丢弃有用的信息，同时减少训练数据样本的数量。

  • 随机过采样- 该技术旨在通过复制少数类中实例的数量来平衡类分布。

Total observations = 5000
Fraudulent Observations = 50
Non-Fraudulent Observations = 4950
Event Rate = 1%

如果我们将 50 个欺诈性观察结果复制 30 次，那么复制少数类观察结果后的欺诈性观察结果将为 1500 个。过采样后新数据中的总观察结果将为 4950+1500 = 6450。因此，新数据集的事件率将为 1500/6450 = 23%。

这种方法的主要优点是不会丢失有用信息。但另一方面，由于它复制了少数类事件，因此过度拟合的可能性增加。

合奏技巧

该方法主要用于修改现有的分类算法，使其适用于不平衡的数据集。在这种方法中，我们从原始数据构建几个两级分类器，然后聚合它们的预测。随机森林分类器是基于集成的分类器的一个示例。