3D 变换
回转
3D 旋转与 2D 旋转不同。在 3D 旋转中,我们必须沿着旋转轴指定旋转角度。我们可以绕 X、Y 和 Z 轴执行 3D 旋转。它们以矩阵形式表示如下 -
$$R_{x}(\theta) = \begin{bmatrix} 1& 0& 0& 0\\ 0& cos\theta & −sin\theta& 0\\ 0& sin\theta & cos\theta& 0\\ 0& 0& 0& 1\ \ \end{bmatrix} R_{y}(\theta) = \begin{bmatrix} cos\theta& 0& sin\theta& 0\\ 0& 1& 0& 0\\ −sin\theta& 0& cos\theta& 0\\ 0& 0& 0& 1\\ \end{bmatrix} R_{z}(\theta) =\begin{bmatrix} cos\theta & −sin\theta & 0& 0\\ sin\theta & cos\theta & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1 \end{bmatrix}$$
下图解释了绕各个轴的旋转 -
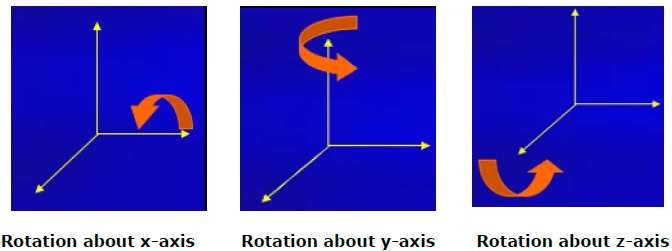
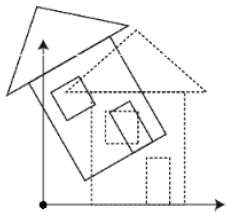
缩放
您可以使用缩放变换来更改对象的大小。在缩放过程中,您可以扩大或压缩对象的尺寸。可以通过将对象的原始坐标乘以缩放因子来实现缩放,以获得所需的结果。下图显示了3D缩放的效果 -
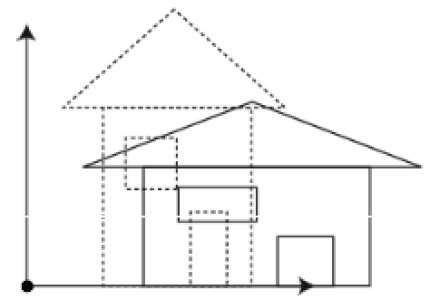
在3D缩放操作中,使用三个坐标。假设原始坐标为(X, Y, Z),缩放因子分别为$(S_{X,} S_{Y,} S_{z})$,生成的坐标为(X', Y' ,Z')。这可以用数学方式表示,如下所示 -
$S = \begin{bmatrix} S_{x}& 0& 0& 0\\ 0& S_{y}& 0& 0\\ 0& 0& S_{z}& 0\\ 0& 0& 0& 1 \end{bmatrix}$
P'=P·S
$[{X}' \:\:\: {Y}' \:\:\: {Z}' \:\:\: 1] = [X \:\:\:Y \:\:\: Z \:\:\: 1] \:\: \begin{bmatrix} S_{x}& 0& 0& 0\\ 0& S_{y}& 0& 0\\ 0& 0& S_{z}& 0\\ 0& 0& 0&1 \end{b矩阵}$
$ = [X.S_{x} \:\:\: Y.S_{y} \:\:\: Z.S_{z} \:\:\: 1]$
剪切
使物体形状倾斜的变换称为剪切变换。与 2D 剪切一样,我们可以在 3D 中沿 X 轴、Y 轴或 Z 轴剪切对象。
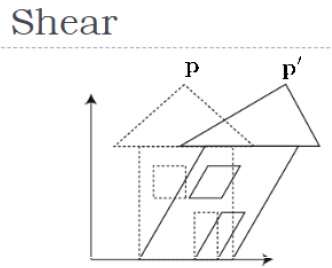
如上图所示,有一个坐标P。你可以剪切它得到一个新的坐标P',它可以用3D矩阵形式表示如下 -
$Sh = \begin{bmatrix} 1 & sh_{x}^{y} & sh_{x}^{z} & 0 \\ sh_{y}^{x} & 1 & sh_{y}^{z} & 0 \\ sh_{z}^{x} & sh_{z}^{y} & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$
P' = P ∙ Sh
$X' = X + Sh_{x}^{y} Y + Sh_{x}^{z} Z$
$Y' = Sh_{y}^{x}X + Y +sh_{y}^{z}Z$
$Z' = Sh_{z}^{x}X + Sh_{z}^{y}Y + Z$
变换矩阵
变换矩阵是变换的基本工具。nxm 维的矩阵与对象的坐标相乘。通常使用 3 x 3 或 4 x 4 矩阵进行变换。例如,考虑以下用于各种操作的矩阵。
| $T = \begin{bmatrix} 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ t_{x}& t_{y}& t_{z}& 1\\ \end{bmatrix}$ | $S = \begin{bmatrix} S_{x}& 0& 0& 0\\ 0& S_{y}& 0& 0\\ 0& 0& S_{z}& 0\\ 0& 0& 0& 1 \end{bmatrix}$ | $Sh = \begin{bmatrix} 1& sh_{x}^{y}& sh_{x}^{z}& 0\\ sh_{y}^{x}& 1 & sh_{y}^{z}& 0\\ sh_{z}^{x}& sh_{z}^{y}& 1& 0\\ 0& 0& 0& 1 \end{bmatrix}$ |
| 翻译矩阵 | 缩放矩阵 | 剪切矩阵 |
| $R_{x}(\theta) = \begin{bmatrix} 1& 0& 0& 0\\ 0& cos\theta & -sin\theta& 0\\ 0& sin\theta & cos\theta& 0\\ 0& 0& 0& 1\\ \结束{b矩阵}$ | $R_{y}(\theta) = \begin{bmatrix} cos\theta& 0& sin\theta& 0\\ 0& 1& 0& 0\\ -sin\theta& 0& cos\theta& 0\\ 0& 0& 0& 1\\ \end {b矩阵}$ | $R_{z}(\theta) = \begin{bmatrix} cos\theta & -sin\theta & 0& 0\\ sin\theta & cos\theta & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1 \结束{b矩阵}$ |
| 旋转矩阵 | ||
