圆生成算法
在屏幕上画一个圆比画一条线稍微复杂一些。有两种流行的生成圆的算法 - Bresenham 算法和中点圆算法。这些算法基于确定绘制圆所需的后续点的思想。让我们详细讨论算法 -
圆的方程为 $X^{2} + Y^{2} = r^{2},$ 其中 r 是半径。
布雷森纳姆算法
我们无法在光栅显示器上显示连续的弧线。相反,我们必须选择最近的像素位置来完成弧线。
从下图中,您可以看到我们已将像素放置在 (X, Y) 位置,现在需要决定将下一个像素放置在何处 - 在 N (X+1, Y) 或 S (X+1, Y-1)。
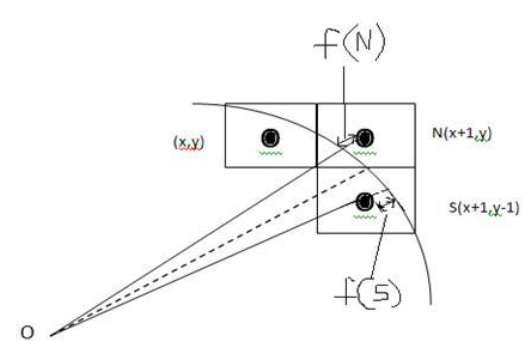
这可以由决策参数d来决定。
- 如果 d <= 0,则选择 N(X+1, Y) 作为下一个像素。
- 如果 d > 0,则选择 S(X+1,Y-1) 作为下一个像素。
算法
步骤 1 - 获取圆心和半径的坐标,并将它们分别存储在 x、y 和 R 中。设置 P=0 且 Q=R。
步骤 2 - 设置决策参数 D = 3 – 2R。
步骤 3 - 当 P ≤ Q 时重复步骤 8。
步骤 4 - 调用画圆 (X, Y, P, Q)。
步骤 5 - 增加 P 的值。
步骤 6 - 如果 D < 0,则 D = D + 4P + 6。
步骤 7 - 否则设置 R = R - 1, D = D + 4(PQ) + 10。
步骤 8 - 调用画圆 (X, Y, P, Q)。
Draw Circle Method(X, Y, P, Q). Call Putpixel (X + P, Y + Q). Call Putpixel (X - P, Y + Q). Call Putpixel (X + P, Y - Q). Call Putpixel (X - P, Y - Q). Call Putpixel (X + Q, Y + P). Call Putpixel (X - Q, Y + P). Call Putpixel (X + Q, Y - P). Call Putpixel (X - Q, Y - P).
中点算法
步骤 1 - 输入半径r和圆心 $(x_{c,} y_{c})$ 并获得以原点为中心的圆圆周上的第一个点:
(x0, y0) = (0, r)
步骤 2 - 计算决策参数的初始值:
$P_{0}$ = 5/4 – r(有关该方程的简化,请参阅以下说明。)
f(x, y) = x2 + y2 - r2 = 0
f(xi - 1/2 + e, yi + 1)
= (xi - 1/2 + e)2 + (yi + 1)2 - r2
= (xi- 1/2)2 + (yi + 1)2 - r2 + 2(xi - 1/2)e + e2
= f(xi - 1/2, yi + 1) + 2(xi - 1/2)e + e2 = 0

Let di = f(xi - 1/2, yi + 1) = -2(xi - 1/2)e - e2
Thus,
If e < 0 then di > 0 so choose point S = (xi - 1, yi + 1).
di+1 = f(xi - 1 - 1/2, yi + 1 + 1) = ((xi - 1/2) - 1)2 + ((yi + 1) + 1)2 - r2
= di - 2(xi - 1) + 2(yi + 1) + 1
= di + 2(yi + 1 - xi + 1) + 1
If e >= 0 then di <= 0 so choose point T = (xi, yi + 1)
di+1 = f(xi - 1/2, yi + 1 + 1)
= di + 2yi+1 + 1
The initial value of di is
d0 = f(r - 1/2, 0 + 1) = (r - 1/2)2 + 12 - r2
= 5/4 - r {1-r can be used if r is an integer}
When point S = (xi - 1, yi + 1) is chosen then
di+1 = di + -2xi+1 + 2yi+1 + 1
When point T = (xi, yi + 1) is chosen then
di+1 = di + 2yi+1 + 1
步骤 3 - 在从 K=0 开始的每个 $X_{K}$ 位置,执行以下测试 -
If PK < 0 then next point on circle (0,0) is (XK+1,YK) and PK+1 = PK + 2XK+1 + 1 Else PK+1 = PK + 2XK+1 + 1 – 2YK+1 Where, 2XK+1 = 2XK+2 and 2YK+1 = 2YK-2.
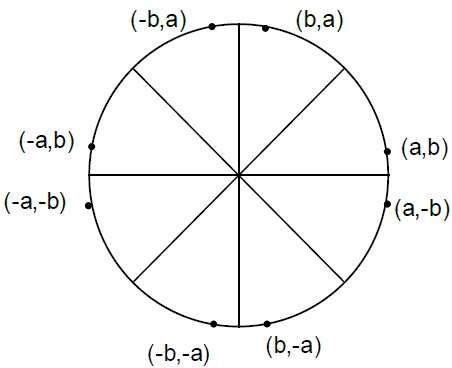
步骤 4 - 确定其他七个八分圆中的对称点。
步骤 5 - 将每个计算像素位置 (X, Y) 移动到以 $(X_{C,} Y_{C})$ 为中心的圆形路径上并绘制坐标值。
X = X + XC, Y = Y + YC
步骤 6 - 重复步骤 3 到 5,直到 X >= Y。
