限制器和电压倍增器

与削波器和钳位器等波形整形电路一起，二极管还用于构建其他电路，例如限制器和电压倍增器，我们将在本章中讨论这些电路。二极管还有另一个重要的应用，称为整流器，稍后将讨论。

限制器

我们在使用这些限幅器和钳位器时经常遇到的另一个名称是限制器电路。限幅电路可以理解为限制输出电压不超过预定值的电路。

这或多或少是一个限幅电路，不允许信号超过指定值。实际上，削波可以被称为极限程度的限制。因此限制可以理解为平滑限幅。

下图显示了限制器电路的一些示例 -

限制器和电压倍增器

限幅器电路的性能可以从其传输特性曲线来了解。此类曲线的示例如下。

传输特性曲线

图表中指定了表示限制器特性的下限和上限。该图的输出电压可以理解为

$$V_{0}= L_{-},KV_{i},L_{+}$$

在哪里

$$L_{-}=V_{i}\leq \frac{L_{-}}{k}$$

$$KV_{i}=\frac{L_{-}}{k}< V_{i}<\frac{L_{+}}{k}$$

$$L_{+}=V_{i}\geq \frac{L_{+}}{K}$$

限制器的类型

限制器有几种类型，例如

  • 单极限制器- 该电路以一种方式限制信号。

  • 双极限制器- 该电路以两种方式限制信号。

  • 软限制器- 即使输入发生微小变化，该电路的输出也可能会发生变化。

  • 硬限幅器- 输出不会轻易随着输入信号的变化而变化。

  • 单限幅器- 该电路采用一个二极管进行限幅。

  • 双限制器- 该电路采用两个二极管进行限制。

电压倍增器

在某些应用中，在某些情况下需要倍增电压。借助使用二极管和电容器的简单电路可以轻松完成此操作。如果电压加倍，这样的电路称为电压倍增器。这可以扩展为三倍电压器或四倍电压器等以获得高直流电压。

为了更好地理解，让我们考虑一个将电压乘以 2 倍的电路。该电路可以称为倍压器。下图所示为倍压器电路。

倍压器

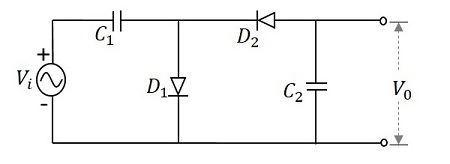
施加的输入电压是正弦波形式的交流信号，如下图所示。

输入波形

在职的

通过分析输入信号的每个半周期就可以理解电压倍增电路。每个周期使二极管和电容器以不同的方式工作。让我们试着理解这一点。

在第一个正半周期内− 当施加输入信号时，电容器 $C_{1}$ 充电，二极管 $D_{1}$ 正向偏置。虽然二极管 $D_{2}$ 反向偏置，但电容器 $C_{2}$ 没有任何电荷。这使得输出 $V_{0}$ 为 $V_{m}$

这可以从下图来理解。

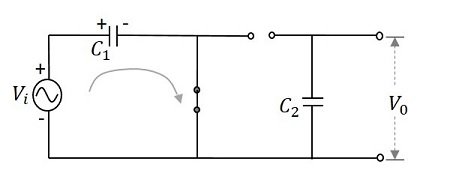
第一个正半周期

因此，在 0 到 $\pi$ 期间，产生的输出电压将为 $V_{max}$。电容器 $C_{1}$ 通过正向偏置二极管 $D_{1}$ 充电以提供输出，而 $C_{2}$ 不充电。该电压出现在输出端。

在负半周期期间- 此后，当负半周期到来时，二极管 $D_{1}$ 获得反向偏置，二极管 $D_{2}$ 获得正向偏置。二极管 $D_{2}$ 通过电容器 $C_{2}$ 获取电荷，电容器在此过程中充电。然后电流流过电容器 $C_{1}$ 进行放电。从下图可以理解。

负半周期

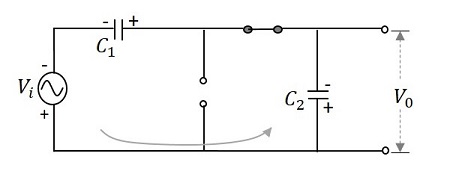
因此，在 $\pi$ 到 $2\pi$ 期间，电容器 $C_{2}$ 两端的电压将为 $V_{max}$。而充满电的电容器$C_{1}$则倾向于放电。现在两个电容器的电压一起出现在输出端，即 $2V_{max}$。因此，该周期内的输出电压$V_{0}$为$2V_{max}$

在下一个正半周期内- 电容器 $C_{1}$ 从电源充电，二极管 $D_{1}$ 获得正向偏置。电容器 $C_{2}$ 保留电荷，因为它找不到放电方式，并且二极管 $D_{2}$ 受到反向偏置。现在，该周期的输出电压 $V_{0}$ 获得两个电容器的电压，它们一起出现在输出端，即 $2V_{max}$。

在下一个负半周期期间- 下一个负半周期使电容器 $C_{1}$ 再次从其完全充电状态放电，并使二极管 $D_{1}$ 反向偏置，而 $D_{2}$ 正向和电容器$C_{2}$ 进一步充电以维持其电压。现在，该周期的输出电压 $V_{0}$ 获得两个电容器的电压，它们一起出现在输出端，即 $2V_{max}$。

因此，输出电压 $V_{0}$ 在整个操作过程中保持为 $2V_{max}$，这使得该电路成为倍压器。

电压倍增器主要用于需要高直流电压的地方。例如，阴极射线管和计算机显示器。

分压器

虽然二极管用于倍增电压，但可以将一组串联电阻制成一个小型网络来分压。这种网络称为分压器网络。

分压器是一种将较大电压变为较小电压的电路。这是使用串联电阻来完成的。输出将是输入的一小部分。输出电压取决于其驱动的负载的电阻。

让我们尝试了解分压器电路的工作原理。下图是一个简单的分压器网络的示例。

分压器

如果我们尝试画出输出电压的表达式，

$$V_{i}=i\left ( R_{1}+R_{2} \right )$$

$$i=\frac{V-{i}}{\left ( R_{1}+R_{2} \right )}$$

$$V_{0}=i \:R_{2}\rightarrow \:i\:=\frac{V_{0}}{R_{2}}$$

两者比较，

$$\frac{V_{0}}{R_{2}}=\frac{V_{i}}{\left ( R_1 + R_{2} \right )}$$

$$V_{0}=\frac{V_{i}}{\left ( R_1 + R_{2} \right )}R_{2}$$

这是获取输出电压值的表达式。因此，输出电压根据网络中电阻器的电阻值进行划分。添加更多电阻器以获得不同输出电压的不同分数。

让我们通过一个示例问题来了解有关分压器的更多信息。

例子

计算输入电压为 10v、两个串联电阻 2kΩ 和 5kΩ 的网络的输出电压。

分压器示例

输出电压 $V_{0}$ 由下式给出

$$V_{0}=\frac{V_{i}}{\left ( R_1 + R_{2} \right )}R_{2}$$

$$=\frac{10}{\left ( 2 + 5 \right )k\Omega }5k\Omega$$

$$=\frac{10}{7}\times 5=\frac{50}{7}$$

$$=7.142v$$

上述问题的输出电压$V_0$为7.14v