
- 电子电路资源
- 电子电路 - 快速指南
- 电子电路 - 资源
- 电子电路 - 讨论
电子电路 - 信号
信号可以理解为“一种表示形式,提供有关产生信号的源中存在的数据的一些信息” 。这通常是随时间变化的。因此,信号可以是传输某些信息的能量源。这可以很容易地用图表表示。
例子
- 闹钟发出信号,表明时间到了。
- 炊具哨声确认食物已煮熟。
- 红灯表示有危险。
- 交通信号指示您的移动。
- 电话铃声响起,表示有呼叫。
信号可以是传达某些信息的任何类型。这种由电子设备产生的信号称为电子信号或电信号。这些通常是时间变体。
信号类型
根据信号的特性,信号可以分为模拟信号或数字信号。模拟信号和数字信号可以进一步分类,如下图所示。

模拟信号
代表随时间变化的量的连续时变信号可以称为模拟信号。该信号根据代表该信号的量的瞬时值,随时间不断变化。
数字信号
本质上是离散的或形式上不连续的信号可以称为数字信号。该信号具有单独表示的单独值,这些值不基于先前的值,就好像它们是在该特定时刻导出的一样。
周期信号和非周期信号
任何在一段时间内重复其模式的模拟或数字信号都称为周期信号。该信号的模式重复连续,并且易于假设或计算。
任何在一段时间内不重复其模式的模拟或数字信号称为非周期信号。该信号具有连续的模式,但该模式不重复并且不那么容易假设或计算。
信号和符号
在周期信号中,最常用的信号有正弦波、余弦波、三角波、方波、矩形波、锯齿波、脉冲波或脉冲串等,让我们看看这些波形。
单位阶跃信号
单位阶跃信号具有从原点到 X 轴上 1 个单位的值。这主要用作测试信号。单位阶跃信号的图像如下所示。

单位阶跃函数用$u\left ( t \right )$ 表示。它定义为 -
$$u\left ( t \right )=\left\{\begin{matrix}1 & t\geq 0\\ 0 & t< 0\end{matrix}\right。$$
单位脉冲信号
单位脉冲信号在其起源处具有一个单位的值。它的面积是一个单位。单位脉冲信号的图像如下所示。

单位脉冲函数用ẟ(t)表示。它被定义为
$$\delta \left ( t \right )=\left\{\begin{matrix} \infty \:\:if \:\:t=0\\0 \:\:if \:\:t\neq 0\结束{矩阵}\右。$$
$$\int_{-\infty }^{\infty }\delta \left ( t \right )d\left ( t \right )=1$$
$$\int_{-\infty }^{t }\delta \left ( t \right )d\left ( t \right )=u\left ( t \right )$$
$$\delta \left ( t \right )=\frac{du\left ( t \right )}{d\left ( t \right )} $$
单位斜坡信号
单位斜坡信号的值从其原点开始呈指数增长。单位斜坡信号的图像如下所示。

单位斜坡函数用u(t)表示。它定义为 -
$$\int_{0}^{t}u\left ( t \right ) d\left ( t \right )=\int_{0}^{t} 1 dt =t=r\left ( t \right ) $$
$$u\left ( t \right )=\frac{dr\left ( t \right )}{dt}$$
单位抛物线信号
单位抛物线信号的值在其原点像抛物线一样变化。单位抛物线信号的图像如下所示。
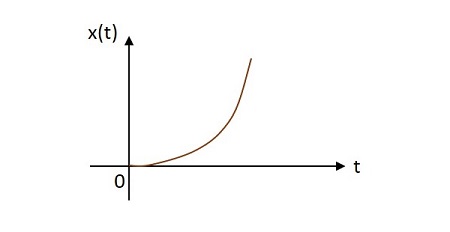
单位抛物线函数用$u\left ( t \right )$ 表示。它定义为 -
$$\int_{0}^{t}\int_{0}^{t}u\left ( t \right )dtdt=\int_{0}^{t}r\left ( t \right )dt=\ int_{0}^{t} t.dt=\frac{t^{2}}{2}dt=x\left ( t \right )$$
$$r\left ( t \right )=\frac{dx\left ( t \right )}{dt}$$
$$u\left ( t \right )=\frac{d^{2}x\left ( t \right )}{dt^{2}}$$
符号函数
Signum 函数的值从其原点开始均匀分布在正平面和负平面上。Signum 函数的图像如下所示。

Signum 函数由sgn(t)表示。它被定义为
$$sgn\left ( t \right )=\left\{\begin{matrix} 1 \:\: 对于 \:\: t\geq 0\\-1 \:\: 对于 \:\:t < 0 \end{矩阵}\right.$$
$$sgn\left ( t \right )=2u\left ( t \right ) -1$$
指数信号
指数信号的值相对于其起源呈指数变化。指数函数的形式为 -
$$x\left ( t \right ) =e^{\alpha t}$$
指数的形状可以由$\alpha$定义。这个函数可以分3种情况来理解
案例 1 -
如果 $\alpha = 0\rightarrow x\left ( t \right )=e^{0}=1$
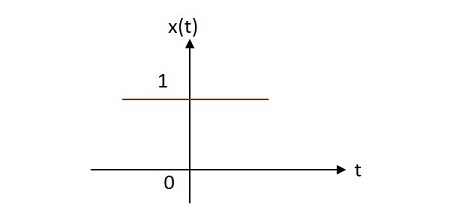
案例 2 -
如果 $\alpha <0$ 则 $x\left ( t \right )=e^{\alpha t}$ 其中 $\alpha$ 为负数。这种形状称为衰减指数。
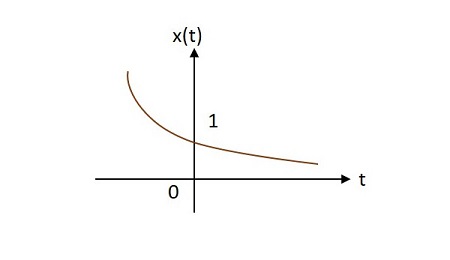
案例 3 -
如果 $\alpha > 0$ 则 $x\left ( t \right )=e^{\alpha t}$ 其中 $\alpha$ 为正。这种形状称为指数上升。
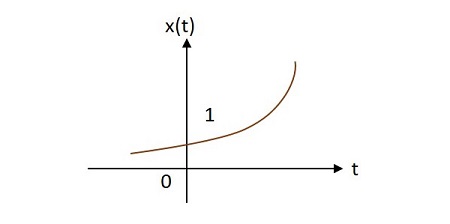
矩形信号
矩形信号的值从其原点开始在正平面和负平面上呈矩形分布。矩形信号的图像如下所示。

矩形函数用$x\left ( t \right )$ 表示。它被定义为
$$x\left ( t \right )=A \:rect\left [ \frac{t}{T} \right ]$$
三角信号
矩形信号的值从其原点开始在正平面和负平面上呈三角形分布。三角信号的图像如下所示。
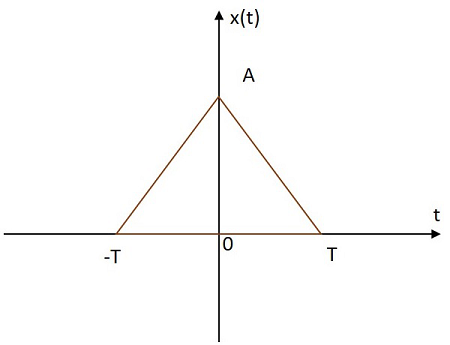
三角函数用$x\left ( t \right )$ 表示。它被定义为
$$x\left ( t \right )=A \left [ 1-\frac{\left | t \right |}{T} \right ]$$
正弦信号
正弦信号的值相对于其原点呈正弦变化。正弦信号的图像如下所示。

正弦函数用 x (t) 表示。它定义为 -
$$x\left ( t \right )=A \cos \left ( w_{0} t\pm \phi \right )$$
或者
$$x\left ( t \right )=A sin\left ( w_{0}t\pm \phi \right )$$
其中 $T_{0}=\frac{2 \pi}{w_{0}}$
正弦函数
Sinc 信号的值根据特定关系变化,如下面给出的等式所示。它在原点处具有最大值,并随着远离而不断减小。Sinc 函数信号的图像如下所示。
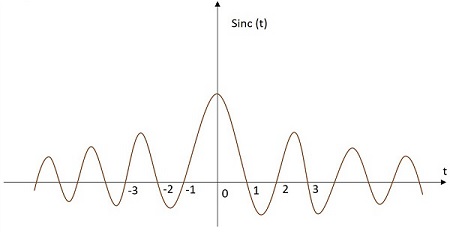
Sinc 函数用sinc(t)表示。它定义为 -
$$sinc\left ( t \right )=\frac{sin\left ( \pi t \right )}{\pi t}$$
这些是我们在电子和通信领域最常遇到的不同信号。每个信号都可以用数学方程来定义,以使信号分析更加容易。
如前所述,每个信号都有特定的波形。波的整形可能会改变信号中存在的内容。不管怎样,是否改变特定电路的波形是由设计工程师决定的。但是,要改变波浪的形状,有一些技术将在进一步的单元中讨论