
- 电子电路资源
- 电子电路 - 快速指南
- 电子电路 - 资源
- 电子电路 - 讨论
电子电路 - 快速指南
电子电路 - 简介
在电子领域,我们有不同的组件来满足不同的目的。根据应用的不同,多种元件可用于多种类型的电路中。
电子元器件
类似于砌墙的砖块,组件是电路的基本砖块。组件是一个基本元素,有助于将想法发展为执行电路。
每个组件都有一些基本属性,并且组件的Behave也会相应变化。使用它们来构建预期电路取决于开发人员的座右铭。下图显示了不同电子电路中使用的电子元件的一些示例。

为了收集一个想法,让我们看一下组件的类型。它们可以是有源组件,也可以是无源组件。
有源元件
有源元件是那些在提供一些外部能量时进行传导的元件。
有源元件以电压或电流的形式产生能量。
示例- 二极管、晶体管、变压器等。
无源元件
无源组件是那些一旦连接就开始运行的组件。它们的运行不需要外部能量。
无源元件以电压或电流的形式存储和维持能量。
示例- 电阻器、电容器、电感器等。
我们还有另一种分类:线性和非线性元件。
线性元件
线性元件或元件是电流和电压之间具有线性关系的元件或元件。
线性元件的参数不随电流和电压而改变。
示例- 二极管、晶体管、变压器等。
非线性元件
非线性元件或组件是电流和电压之间具有非线性关系的元件或组件。
非线性元件的参数随电流和电压而变化。
示例- 电阻器、电容器、电感器等。
这些是用于各种目的的组件,它们一起可以执行它们所构建的首选任务。这种不同组件的组合称为电路。
电子电路
当以特定方式出于某种目的连接一定数量的元件时,就形成了电路。电路是不同组件的网络。有不同类型的电路。
下图显示了不同类型的电子电路。它显示了印刷电路板,印刷电路板是连接在板上的一组电子电路。

电子电路可以根据其操作、连接、结构等分为不同的类别。让我们更多地讨论电子电路的类型。
有源电路
使用有源元件构建的电路称为有源电路。
它通常包含一个电源,电路从中提取更多功率并将其输送到负载。
额外的功率被添加到输出中,因此输出功率始终大于所施加的输入功率。
功率增益将始终大于单位。
无源电路
使用无源元件构建的电路称为无源电路。
即使它包含电源,该电路也不会提取任何功率。
附加功率不会添加到输出中,因此输出功率始终小于所施加的输入功率。
功率增益将始终小于单位。
电子电路也可分为模拟电路、数字电路或混合电路。
模拟电路
模拟电路可以是其中具有线性元件的电路。因此它是一个线性电路。
模拟电路具有连续电压范围的模拟信号输入。
数字电路
数字电路可以是其中含有非线性元件的电路。因此它是一个非线性电路。
它只能处理数字信号。
数字电路具有离散值的数字信号输入。
混合信号电路
混合信号电路可以是同时具有线性和非线性组件的电路。因此它被称为混合信号电路。
这些电路由模拟电路和微处理器组成,用于处理输入。
根据连接类型,电路可分为串联电路或并联电路。串联电路是串联连接的电路,并联电路是其组件并联连接的电路。
现在我们对电子元件有了基本的了解,让我们继续讨论它们的用途,这将帮助我们为不同的应用构建更好的电路。无论电子电路的目的是什么(处理、发送、接收、分析),该过程都是以信号的形式执行的。在下一章中,我们将讨论电子电路中存在的信号和信号类型。
电子电路 - 信号
信号可以理解为“一种表示形式,提供有关产生信号的源中存在的数据的一些信息” 。这通常是随时间变化的。因此,信号可以是传输某些信息的能量源。这可以很容易地用图表表示。
例子
- 闹钟发出信号,表明时间到了。
- 炊具哨声确认食物已煮熟。
- 红灯表示有危险。
- 交通信号指示您的移动。
- 电话铃声响起,表示有呼叫。
信号可以是传达某些信息的任何类型。这种由电子设备产生的信号称为电子信号或电信号。这些通常是时间变体。
信号类型
根据信号的特性,信号可以分为模拟信号或数字信号。模拟信号和数字信号可以进一步分类,如下图所示。

模拟信号
代表随时间变化的量的连续时变信号可以称为模拟信号。该信号根据代表该信号的量的瞬时值,随时间不断变化。
数字信号
本质上是离散的或形式上不连续的信号可以称为数字信号。该信号具有单独表示的单独值,这些值不基于先前的值,就好像它们是在该特定时刻导出的一样。
周期信号和非周期信号
任何在一段时间内重复其模式的模拟或数字信号都称为周期信号。该信号的模式重复连续,并且易于假设或计算。
任何在一段时间内不重复其模式的模拟或数字信号称为非周期信号。该信号具有连续的模式,但该模式不重复并且不那么容易假设或计算。
信号和符号
在周期信号中,最常用的信号有正弦波、余弦波、三角波、方波、矩形波、锯齿波、脉冲波或脉冲串等,让我们看看这些波形。
单位阶跃信号
单位阶跃信号具有从原点到 X 轴上 1 个单位的值。这主要用作测试信号。单位阶跃信号的图像如下所示。

单位阶跃函数用$u\left ( t \right )$ 表示。它定义为 -
$$u\left ( t \right )=\left\{\begin{matrix}1 & t\geq 0\\ 0 & t< 0\end{matrix}\right。$$
单位脉冲信号
单位脉冲信号在其起源处具有一个单位的值。它的面积是一个单位。单位脉冲信号的图像如下所示。

单位脉冲函数用ẟ(t)表示。它被定义为
$$\delta \left ( t \right )=\left\{\begin{matrix} \infty \:\:if \:\:t=0\\0 \:\:if \:\:t\neq 0\结束{矩阵}\右。$$
$$\int_{-\infty }^{\infty }\delta \left ( t \right )d\left ( t \right )=1$$
$$\int_{-\infty }^{t }\delta \left ( t \right )d\left ( t \right )=u\left ( t \right )$$
$$\delta \left ( t \right )=\frac{du\left ( t \right )}{d\left ( t \right )} $$
单位斜坡信号
单位斜坡信号的值从其原点开始呈指数增长。单位斜坡信号的图像如下所示。

单位斜坡函数用u(t)表示。它定义为 -
$$\int_{0}^{t}u\left ( t \right ) d\left ( t \right )=\int_{0}^{t} 1 dt =t=r\left ( t \right ) $$
$$u\left ( t \right )=\frac{dr\left ( t \right )}{dt}$$
单位抛物线信号
单位抛物线信号的值在其原点像抛物线一样变化。单位抛物线信号的图像如下所示。
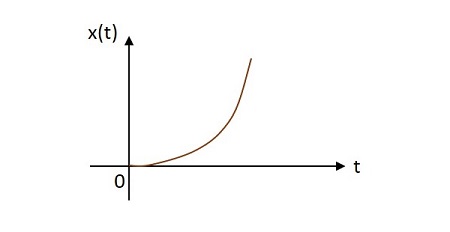
单位抛物线函数用$u\left ( t \right )$ 表示。它定义为 -
$$\int_{0}^{t}\int_{0}^{t}u\left ( t \right )dtdt=\int_{0}^{t}r\left ( t \right )dt=\ int_{0}^{t} t.dt=\frac{t^{2}}{2}dt=x\left ( t \right )$$
$$r\left ( t \right )=\frac{dx\left ( t \right )}{dt}$$
$$u\left ( t \right )=\frac{d^{2}x\left ( t \right )}{dt^{2}}$$
符号函数
Signum 函数的值从其原点开始均匀分布在正平面和负平面上。Signum 函数的图像如下所示。

Signum 函数由sgn(t)表示。它被定义为
$$sgn\left ( t \right )=\left\{\begin{matrix} 1 \:\: 对于 \:\: t\geq 0\\-1 \:\: 对于 \:\:t < 0 \end{矩阵}\right.$$
$$sgn\left ( t \right )=2u\left ( t \right ) -1$$
指数信号
指数信号的值相对于其起源呈指数变化。指数函数的形式为 -
$$x\left ( t \right ) =e^{\alpha t}$$
指数的形状可以由$\alpha$定义。这个函数可以分3种情况来理解
案例 1 -
如果 $\alpha = 0\rightarrow x\left ( t \right )=e^{0}=1$
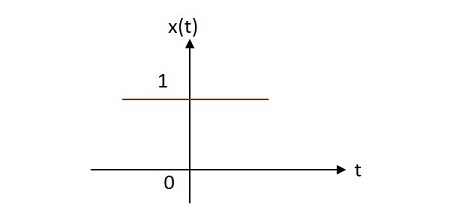
案例 2 -
如果 $\alpha <0$ 则 $x\left ( t \right )=e^{\alpha t}$ 其中 $\alpha$ 为负数。这种形状称为衰减指数。
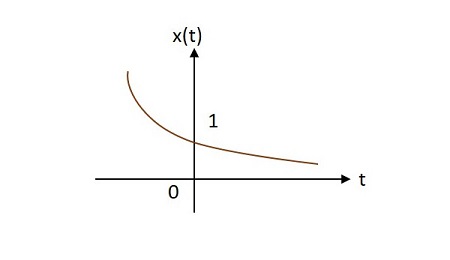
案例 3 -
如果 $\alpha > 0$ 则 $x\left ( t \right )=e^{\alpha t}$ 其中 $\alpha$ 为正。这种形状称为指数上升。
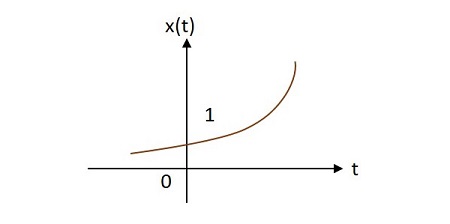
矩形信号
矩形信号的值从其原点开始在正平面和负平面上呈矩形分布。矩形信号的图像如下所示。

矩形函数用$x\left ( t \right )$ 表示。它被定义为
$$x\left ( t \right )=A \:rect\left [ \frac{t}{T} \right ]$$
三角信号
矩形信号的值从其原点开始在正平面和负平面上呈三角形分布。三角信号的图像如下所示。
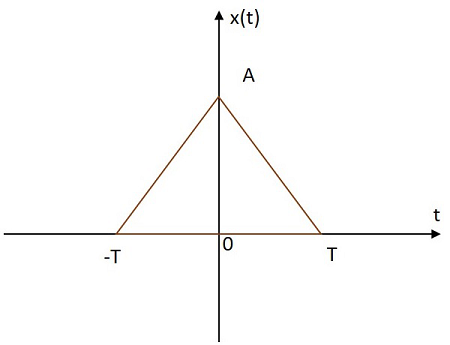
三角函数用$x\left ( t \right )$ 表示。它被定义为
$$x\left ( t \right )=A \left [ 1-\frac{\left | t \right |}{T} \right ]$$
正弦信号
正弦信号的值相对于其原点呈正弦变化。正弦信号的图像如下所示。

正弦函数用 x (t) 表示。它定义为 -
$$x\left ( t \right )=A \cos \left ( w_{0} t\pm \phi \right )$$
或者
$$x\left ( t \right )=A sin\left ( w_{0}t\pm \phi \right )$$
其中 $T_{0}=\frac{2 \pi}{w_{0}}$
正弦函数
Sinc 信号的值根据特定关系变化,如下面给出的等式所示。它在原点处具有最大值,并随着远离而不断减小。Sinc 函数信号的图像如下所示。
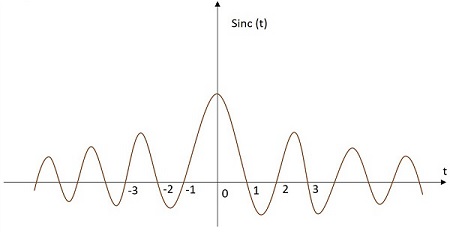
Sinc 函数用sinc(t)表示。它定义为 -
$$sinc\left ( t \right )=\frac{sin\left ( \pi t \right )}{\pi t}$$
这些是我们在电子和通信领域最常遇到的不同信号。每个信号都可以用数学方程来定义,以使信号分析更加容易。
如前所述,每个信号都有特定的波形。波的整形可能会改变信号中存在的内容。不管怎样,是否改变特定电路的波形是由设计工程师决定的。但是,要改变波浪的形状,有一些技术将在进一步的单元中讨论
电子电路 - 线性波形整形
信号也可以称为波。当用图表表示时,每个波浪都有一定的形状。该形状可以是不同的类型,例如正弦曲线、正方形、三角形等,其随时间段而变化,或者它们可以具有一些不考虑时间段的随机形状。
波形整形的类型
波形整形有两种主要类型。他们是 -
- 线性波形整形
- 非线性波形整形
线性波形整形
在这种线性波形整形中,采用电阻器、电容器和电感器等线性元件来整形信号。正弦波输入具有正弦波输出,因此非正弦输入更重要地用于理解线性波整形。
滤波是衰减不需要的信号或再现特定信号的频率分量的选定部分的过程。
过滤器
在信号整形的过程中,如果感觉信号的某些部分不需要,可以使用滤波器电路将其截断。滤波器是一种可以去除输入信号中不需要的部分的电路。信号强度降低的过程也称为衰减。
我们几乎没有什么组件可以帮助我们进行过滤技术。
电容器具有允许交流电和阻止直流电的特性
电感器具有允许直流电但阻止交流电的特性。
利用这些特性,这两个组件特别用于阻止或允许交流或直流。可以根据这些属性来设计滤波器。
我们有四种主要类型的过滤器 -
- 低通滤波器
- 高通滤波器
- 带通滤波器
- 带阻滤波器
现在让我们详细讨论这些类型的过滤器。
低通滤波器
允许一组频率低于指定值的滤波器电路可称为低通滤波器。该滤波器通过较低频率。使用RC和RL的低通滤波器的电路图如下所示。
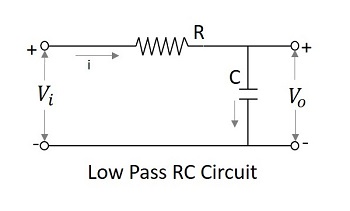
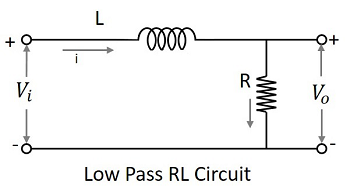
电容滤波器或RC滤波器和电感滤波器或 RL 滤波器均充当低通滤波器。
RC 滤波器- 由于电容器并联,其允许的交流电接地。这会绕过所有高频分量,同时允许输出直流。
RL 滤波器- 由于电感器串联,因此允许直流电进入输出。电感器会阻挡输出端不允许的交流电。
低通滤波器 (LPF) 的符号如下所示。

频率响应
实际滤波器的频率响应如下所示,在不考虑电子元件的实际考虑因素时,理想LPF的频率响应如下所示。
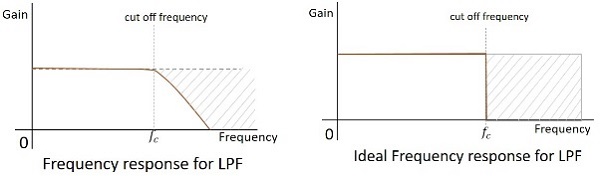
任何滤波器的截止频率都是滤波器用于衰减(截止)信号的临界频率 $f_{c}$。理想的滤波器具有完美的截止,而实用的滤波器几乎没有限制。
RLC 滤波器
在了解了 RC 和 RL 滤波器之后,人们可能会想到最好添加这两个电路以获得更好的响应。下图显示了 RLC 电路的样子。

输入端的信号通过电感器,该电感器阻止交流电并允许直流电。现在,该输出再次通过并联电容器,该电容器将信号中存在的剩余交流分量(如果有)接地,从而允许输出出现直流电。因此,我们在输出端有一个纯直流电。这是比它们都更好的低通电路。
高通滤波器
允许一组频率高于指定值的滤波器电路可称为高通滤波器。该滤波器通过较高频率。使用RC和RL的高通滤波器的电路图如下所示。


电容滤波器或RC滤波器和电感滤波器或RL滤波器都充当高通滤波器。
RC 滤波器
由于电容器串联放置,它会阻挡直流分量并允许交流分量输出。因此,高频分量出现在电阻器的输出端。
强化学习滤波器
由于电感并联,因此允许直流接地。剩余的交流分量出现在输出处。高通滤波器 (HPF) 的符号如下所示。
频率响应
实际滤波器的频率响应如下所示,在不考虑电子元件的实际考虑因素时,理想 HPF 的频率响应如下所示。

任何滤波器的截止频率都是滤波器用于衰减(截止)信号的临界频率 $f_{c}$。理想的滤波器具有完美的截止,而实用的滤波器几乎没有限制。
RLC 滤波器
在了解了 RC 和 RL 滤波器之后,人们可能会想到最好添加这两个电路以获得更好的响应。下图显示了 RLC 电路的样子。
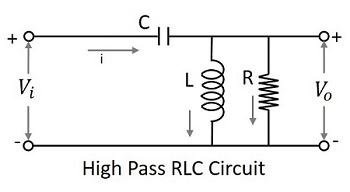
输入端的信号通过电容器,该电容器阻止直流并允许交流。现在,该输出再次通过并联的电感器,该电感器将信号中存在的剩余直流分量(如果有)接地,从而允许输出端出现交流电。因此,我们在输出端有一个纯交流电。这是比它们都更好的高通电路。
带通滤波器
允许一组频率位于两个指定值之间的滤波器电路可称为带通滤波器。该滤波器通过一个频带。
由于我们需要剔除少量的低频和高频,以选择一组指定的频率,因此我们需要级联一个HPF和一个LPF来得到一个BPF。即使通过观察频率响应曲线也可以很容易地理解这一点。
带通滤波器的电路图如下所示。
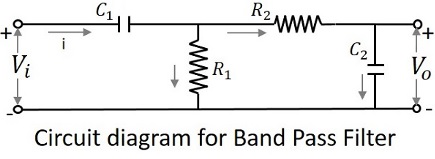
上述电路还可以使用RL电路或RLC电路来构造。上面是为了简单理解而选择的RC电路。
带通滤波器 (BPF) 的符号如下所示。

频率响应
实际滤波器的频率响应如下所示,在不考虑电子元件的实际考虑因素时,理想 BPF 的频率响应如下所示。

任何滤波器的截止频率都是滤波器用于衰减(截止)信号的临界频率 $f_{c}$。理想的滤波器具有完美的截止,而实用的滤波器几乎没有限制。
带阻滤波器
阻止或衰减两个指定值之间的一组频率的滤波器电路可称为带阻滤波器。该滤波器抑制一个频带,因此也可以称为带阻滤波器。
由于我们需要剔除少量的低频和高频,以选择一组指定的频率,因此我们需要级联一个LPF和一个HPF来得到BSF。即使通过观察频率响应曲线也可以很容易地理解这一点。
带阻滤波器的电路图如下所示。

上述电路还可以使用RL电路或RLC电路来构造。上面是为了简单理解而选择的RC电路。
带阻滤波器 (BSF) 的符号如下所示。
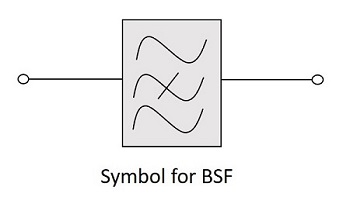
频率响应
实际滤波器的频率响应如下所示,当不考虑电子元件的实际考虑时,理想 BSF 的频率响应如下所示。

任何滤波器的截止频率都是滤波器用于衰减(截止)信号的临界频率 $f_{c}$。理想的滤波器具有完美的截止,而实用的滤波器几乎没有限制。
LPF和HPF的特殊功能
低通和高通滤波器电路在许多应用中用作特殊电路。低通滤波器(LPF)可以用作积分器,而高通滤波器(HPF)可以用作微分器。这两个数学函数只有使用这些电路才可能实现,这减少了电子工程师在许多应用中的工作量。
低通滤波器作为积分器
在低频下,容抗趋于无穷大,在高频下,电抗变为零。因此,在低频下,LPF 具有有限输出,而在高频下,输出为零,这对于积分器电路来说是相同的。因此,低通滤波器可以说是作为积分器工作的。
让 LPF 充当积分器
$$\tau \gg T$$
其中$\tau = RC$ 电路的时间常数
那么C上的电压变化就非常小。
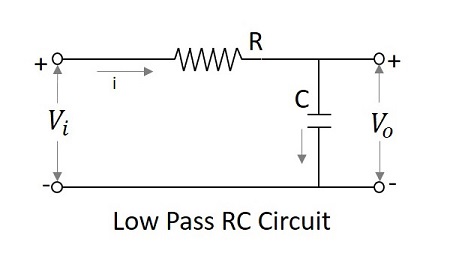
$$V_{i}=iR+\frac{1}{C} \int i \:dt$$
$$V_{i}\cong iR$$
$$自 \:\: \frac{1}{C} \int i \:dt \ll iR$$
$$i=\frac{V_{i}}{R}$$
$$ 自 \:\: V_{0}=\frac{1}{C}\int i dt =\frac{1}{RC}\int V_{i}dt=\frac{1}{\tau } \int V_{i} dt$$
$$输出 \propto \int 输入$$
因此,具有大时间常数的 LPF 产生的输出与输入的积分成正比。
频率响应
实际低通滤波器用作积分器时的频率响应如下所示。

输出波形
如果给积分器电路输入正弦波,则输出将为余弦波。如果输入是方波,则输出波形将改变其形状并如下图所示。

作为微分器的高通滤波器
在低频下,微分器的输出为零,而在高频下,其输出具有某个有限值。这与微分器相同。因此,高通滤波器被称为微分器。
如果 RC HPF 的时间常数远小于输入信号的时间周期,则电路将充当微分器。那么与 C 上的压降相比,R 上的压降非常小。

$$V_{i}=\frac{1}{C}\int i \:dt +iR$$
但 $iR=V_{0}$ 很小
$$自 V_{i}=\frac{1}{C}\int i \:dt$$
$$i=\frac{V_{0}}{R}$$
$$自 \: V_{i} =\frac{1}{\tau }\int V_{0} \:dt$$
其中$\tau =RC$ 电路的时间常数。
两边微分,
$$\frac{dV_{i}}{dt}=\frac{V_0}{\tau }$$
$$V_{0}=\tau \frac{dV_{i}}{dt}$$
$$自 \:V_{0}\propto \frac{dV_{i}}{dt}$$
输出与输入信号的微分成正比。
频率响应
实际高通滤波器用作微分器时的频率响应如下所示。

输出波形
如果微分器电路的输入为正弦波,则输出将为余弦波。如果输入是方波,则输出波形将改变其形状并如下图所示。

这两种电路主要用于各种电子应用中。当施加的输入趋于稳定变化时,微分器电路会产生恒定的输出电压。当施加的输入电压恒定时,积分器电路会产生稳定变化的输出电压。
非线性波形整形
与电阻器一起,非线性元件(例如二极管)用于非线性波形整形电路,以获得所需的改变输出。在非线性波形整形中,要么衰减波形,要么改变波形的直流电平。
使用非线性元件从正弦输入产生非正弦输出波形的过程称为非线性波形整形。
限幅器电路
限幅器电路是一种拒绝指定输入波部分而允许其余部分的电路。高于或低于所确定的截止电压的波形部分被削除或截断。
限幅电路由线性和非线性元件(如电阻器和二极管)组成,但不包括储能元件(如电容器)。这些限幅电路由于其优点而具有许多应用。
限幅电路的主要优点是消除幅度中存在的不需要的噪声。
它们可以用作方波转换器,因为它们可以通过限幅将正弦波转换为方波。
所需波的幅度可以保持在恒定水平。
在二极管限幅器中,两种主要类型是正限幅器和负限幅器。我们将在接下来的两章中讨论这两种类型的剪刀。
电子电路 - 正限幅电路
旨在衰减输入信号的正部分的限幅器电路可称为正限幅器。在正二极管限幅电路中,我们有以下类型 -
- 正系列剪子
- 具有正 $V_{r}$(参考电压)的正串联限幅器
- 具有负 $V_{r}$ 的正系列限幅器
- 正分流限幅器
- 具有正 $V_{r}$ 的正分流限幅器
- 具有负 $V_{r}$ 的正分流限幅器
让我们详细讨论每种类型。
正系列剪子
削波器电路中的二极管串联连接到输入信号并衰减波形的正部分,称为正串联削波器。下图表示正串联限幅器的电路图。
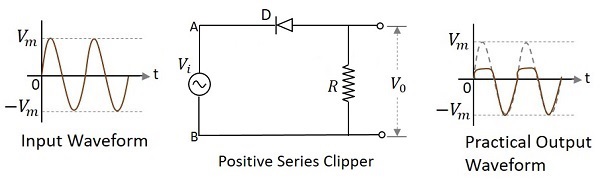
输入的正周期- 当施加输入电压时,输入的正周期使电路中的 A 点相对于 B 点为正。这使得二极管反向偏置,因此它的Behave就像一个打开的开关。因此,由于没有电流流过负载电阻,负载电阻两端的电压变为零,因此 $V_{0}$ 将为零。
输入的负周期- 输入的负周期使电路中的 A 点相对于 B 点为负。这使得二极管正向偏置,因此它像闭合开关一样传导。因此,负载电阻两端的电压将等于所施加的输入电压,因为它完全出现在输出 $V_{0}$ 上。
波形
在上图中,如果观察波形,我们可以了解到只有一部分正峰值被削波。这是因为 V0 两端的电压。但理想的输出并不意味着如此。让我们看看下面的数字。

与理想输出不同,由于二极管导通电压为 0.7v,因此实际输出中存在正周期的比特部分。因此,实际输出波形和理想输出波形会有差异。
具有正 $V_{r}$ 的正系列限幅器
限幅器电路中,二极管串联连接到输入信号,并用正参考电压 $V_{r}$ 偏置,并衰减波形的正部分,称为具有正 $V_{r} 的正串联限幅器$。下图表示当施加的参考电压为正时,正串联限幅器的电路图。

在输入的正周期期间,二极管获得反向偏置,并且参考电压出现在输出处。在其负周期期间,二极管获得正向偏置并像闭合开关一样传导。因此输出波形如上图所示。
具有负 $V_{r}$ 的正系列限幅器
限幅器电路中,二极管串联连接到输入信号,并以负参考电压 $V_{r}$ 偏置,并衰减波形的正部分,称为具有负 $V_{r} 的正串联限幅器$。下图表示当施加的参考电压为负时,正串联限幅器的电路图。

在输入的正周期期间,二极管获得反向偏置,并且参考电压出现在输出处。由于参考电压为负,因此显示出具有恒定幅度的相同电压。在其负周期期间,二极管获得正向偏置并像闭合开关一样传导。因此,大于参考电压的输入信号出现在输出处。
正分流限幅器
限幅器电路中的二极管并联连接到输入信号并衰减波形的正部分,称为正分流限幅器。下图表示正并联限幅器的电路图。

输入的正周期- 当施加输入电压时,输入的正周期使电路中的 A 点相对于 B 点为正。这使得二极管正向偏置,因此它像闭合开关一样传导。因此,由于没有电流流过负载电阻,负载电阻两端的电压变为零,因此 $V_{0}$ 将为零。
输入的负周期- 输入的负周期使电路中的 A 点相对于 B 点为负。这使得二极管反向偏置,因此它的Behave就像一个打开的开关。因此,负载电阻两端的电压将等于所施加的输入电压,因为它完全出现在输出 $V_{0}$ 上。
波形
在上图中,如果观察波形,我们可以了解到只有一部分正峰值被削波。这是由于 $V_{0}$ 两端的电压造成的。但理想的输出并不意味着如此。让我们看看下面的数字。

与理想输出不同,由于二极管导通电压为 0.7v,因此实际输出中存在正周期的比特部分。因此,实际输出波形和理想输出波形会有差异。
具有正 $V_{r}$ 的正分流限幅器
限幅器电路中,二极管并联连接到输入信号,并用正参考电压 $V_{r}$ 进行偏置,并衰减波形的正部分,称为具有正 $V_{r} 的正分流限幅器$。下图表示当施加的参考电压为正时,正并联限幅器的电路图。

在输入的正周期期间,二极管获得正向偏置,并且输出上只出现参考电压。在其负周期期间,二极管受到反向偏置并表现为开路开关。整个输入出现在输出处。因此输出波形如上图所示。
具有负 $V_{r}$ 的正分流限幅器
限幅器电路中,二极管并联连接到输入信号,并用负参考电压 $V_{r}$ 偏置,并衰减波形的正部分,称为具有负 $V_{r} 的正分流限幅器$。
下图表示当施加的参考电压为负时,正并联限幅器的电路图。

在输入的正周期期间,二极管获得正向偏置,并且参考电压出现在输出处。由于参考电压为负,因此显示出具有恒定幅度的相同电压。在其负周期期间,二极管受到反向偏置并表现为开路开关。因此,大于参考电压的输入信号出现在输出处。
电子电路 - 负限幅电路
旨在衰减输入信号的负部分的限幅器电路可称为负限幅器。在负二极管限幅电路中,我们有以下类型。
- 负系列快剪
- 具有正 $V_{r}$(参考电压)的负串联限幅器
- 具有负 $V_{r}$ 的负系列限幅器
- 负分流限幅器
- 具有正 $V_{r}$ 的负分流限幅器
- 具有负 $V_{r}$ 的负分流限幅器
让我们详细讨论每种类型。
负系列快剪
削波器电路中的二极管串联连接到输入信号并衰减波形的负部分,称为负串联削波器。下图表示负串联限幅器的电路图。

输入的正周期- 当施加输入电压时,输入的正周期使电路中的 A 点相对于 B 点为正。这使得二极管正向偏置,因此它的作用就像一个闭合开关。因此,输入电压完全出现在负载电阻上,以产生输出$V_{0}$。
输入的负周期- 输入的负周期使电路中的 A 点相对于 B 点为负。这使得二极管反向偏置,因此它的作用就像一个打开的开关。因此,负载电阻两端的电压将为零,使得 $V_{0}$ 为零。
波形
在上图中,如果观察波形,我们可以了解到只有一部分负峰值被削波。这是由于 $V_{0}$ 两端的电压造成的。但理想的输出并不意味着如此。让我们看看下面的数字。
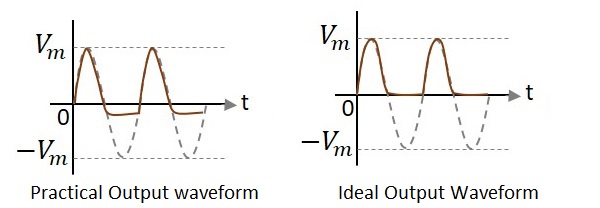
与理想输出不同,由于二极管导通电压为 0.7V,因此实际输出中存在负周期的比特部分。因此,实际输出波形和理想输出波形会有差异。
具有正 $V_{r}$ 的负系列限幅器
限幅器电路中,二极管串联连接到输入信号,并用正参考电压 $V_{r}$ 偏置,并衰减波形的负部分,称为具有正 $V_{r} 的负串联限幅器$。下图表示当施加的参考电压为正时,负串联限幅器的电路图。
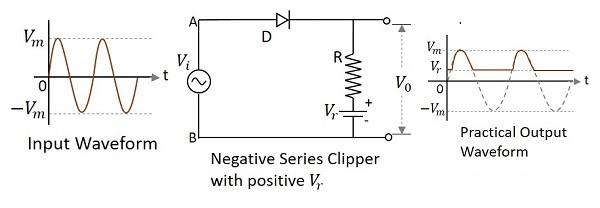
在输入的正周期期间,只有当二极管的阳极电压值超过二极管的阴极电压值时,二极管才开始导通。由于阴极电压等于所施加的参考电压,输出将如图所示。
具有负 $V_{r}$ 的负系列限幅器
限幅器电路中,二极管串联连接到输入信号,并以负参考电压 $V_{r}$ 偏置,并衰减波形的负部分,称为具有负 $V_{r} 的负串联限幅器$。下图表示当施加的参考电压为负时,负串联限幅器的电路图。

在输入的正周期期间,二极管获得正向偏置,并且输入信号出现在输出处。在其负周期期间,二极管受到反向偏置,因此不会导通。但所施加的负参考电压出现在输出端。因此,输出波形的负周期在此参考电平之后被削波。
负分流限幅器
限幅器电路中的二极管并联连接到输入信号并衰减波形的负部分,称为负分流限幅器。下图表示负并联限幅器的电路图。

输入的正周期- 当施加输入电压时,输入的正周期使电路中的 A 点相对于 B 点为正。这使得二极管反向偏置,因此它的Behave就像一个打开的开关。因此,负载电阻两端的电压等于所施加的输入电压,因为它完全出现在输出 $V_{0}$ 上
输入的负周期- 输入的负周期使电路中的 A 点相对于 B 点为负。这使得二极管正向偏置,因此它像闭合开关一样传导。因此,由于没有电流流过负载电阻,负载电阻两端的电压变为零。
波形
在上图中,如果观察波形,我们可以理解,只有一部分负峰值被削波。这是由于 $V_{0}$ 两端的电压造成的。但理想的输出并不意味着如此。让我们看看下面的数字。
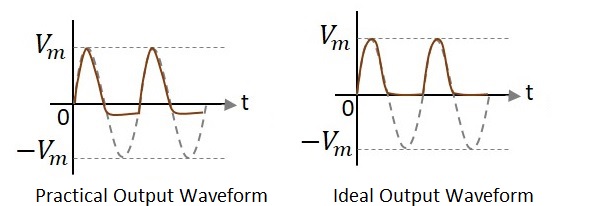
与理想输出不同,由于二极管导通电压为 0.7V,因此实际输出中存在负周期的比特部分。因此,实际输出波形和理想输出波形会有差异。
具有正 $V_{r}$ 的负分流限幅器
在限幅器电路中,二极管并联连接到输入信号,并用正参考电压 $V_{r}$ 进行偏置,并衰减波形的负部分,称为具有正 $V_{r} 的负分流限幅器$。下图表示当施加的参考电压为正时负并联限幅器的电路图。

在输入的正周期期间,二极管受到反向偏置并表现为打开的开关。因此,大于所施加的参考电压的整个输入电压出现在输出端。低于参考电压电平的信号被削除。
在负半周期期间,当二极管正向偏置并且环路完成时,不存在输出。
具有负 $V_{r}$ 的负分流限幅器
限幅器电路中的二极管并联连接到输入信号并使用负参考电压 $V_{r}$ 进行偏置,并衰减波形的负部分,称为具有负 $V_{r} 的负分流限幅器$。下图表示当施加的参考电压为负时,负并联限幅器的电路图。

在输入的正周期期间,二极管受到反向偏置并表现为打开的开关。因此,整个输入电压出现在输出 $V_{o}$ 上。在负半周期期间,二极管正向偏置。高达参考电压的负电压到达输出,剩余信号被削除。
双向剪子
这是一个具有参考电压 $V_{r}$ 的正负限幅器。输入电压通过两个参考电压对输入波形的正负部分进行双向限幅。为此,两个二极管 $D_{1}$ 和 $D_{2}$ 以及两个参考电压 $V_{r1}$ 和 $V_{r2}$ 连接在电路中。
该电路也称为组合限幅器电路。下图显示了两路或组合限幅器电路的电路布置及其输出波形。

在输入信号的正半部分期间,二极管 $D_{1}$ 导通,使参考电压 $V_{r1}$ 出现在输出端。在输入信号的负半部分期间,二极管 $D_{2}$ 导通,使参考电压 $V_{r1}$ 出现在输出端。因此,两个二极管交替导通,以在两个周期期间削波输出。输出通过负载电阻获取。
至此,我们就完成了主要的限幅器电路。让我们在下一章讨论钳位电路。
电子电路 - 钳位电路
钳位电路是一种将直流电平添加到交流信号的电路。实际上,可以使用钳位电路将信号的正峰值和负峰值置于所需的电平。当直流电平发生偏移时,钳位电路称为电平移位器。
钳位电路由电容器等能量存储元件组成。一个简单的钳位电路由电容器、二极管、电阻器和直流电池(如果需要)组成。
钳位电路
钳位电路可以定义为由二极管、电阻器和电容器组成的电路,可将波形移至所需的直流电平,而不改变所施加信号的实际外观。
为了维持波形的时间周期,tau必须大于时间周期的一半(电容器的放电时间应该很慢。)
$$\tau = Rc$$
在哪里
- R 是所用电阻的阻值
- C是所用电容器的电容
电容器充电和放电的时间常数决定了钳位电路的输出。
在钳位电路中,输出波形相对于输入信号发生向上或向下的垂直偏移。
负载电阻和电容影响波形。因此,电容器的放电时间应足够大。
当使用电容器耦合网络时(作为电容器阻挡直流),输入中存在的直流分量被抑制。因此,当需要恢复直流时,需要使用钳位电路。
夹具类型
钳位电路有几种类型,例如
- 正向钳位器
- 带正 $V_r$ 的正钳位器
- 带负 $V_r$ 的正钳位器
- 负钳位器
- 负钳位器与正 $V_{r}$
- 具有负 $V_{r}$ 的负钳位器
让我们详细了解一下它们。
正钳位电路
钳位电路恢复直流电平。当信号的负峰值升高至零电平以上时,该信号被称为正钳位。
正钳位电路由二极管、电阻器和电容器组成,它将输出信号移至输入信号的正部分。下图解释了正钳位电路的结构。
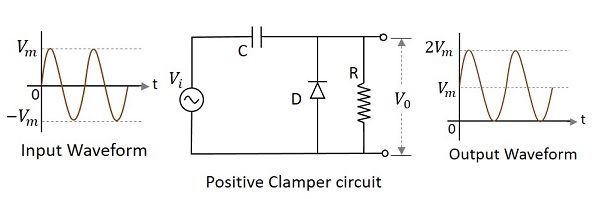
最初,当给定输入时,电容器尚未充电,并且二极管反向偏置。此时不考虑输出。在负半周期期间,在峰值处,电容器在一个板上带负电,在另一板上带正电。电容器现在充电至其峰值 $V_{m}$。该二极管正向偏置并且导电严重。
在下一个正半周期期间,电容器充电至正 Vm,同时二极管获得反向偏置并开路。此时电路的输出为
$$V_{0}=V_{i}+V_{m}$$
因此,信号被正向钳位,如上图所示。输出信号根据输入的变化而变化,但随着输入电压的增加,电平会根据电容器上的电荷而变化。
具有正 V r的正钳位器
正钳位电路如果用某个正参考电压偏置,该电压将被添加到输出以提高钳位电平。利用这一点,具有正参考电压的正钳位器电路构造如下。

在正半周期期间,参考电压通过二极管施加在输出端,并且随着输入电压的增加,二极管的阴极电压相对于阳极电压增加,因此它停止导通。在负半周期期间,二极管获得正向偏置并开始导通。电容器两端的电压和参考电压共同维持输出电压电平。
带负 $V_{r}$ 的正钳位器
正钳位电路如果用一些负参考电压偏置,该电压将被添加到输出以提高钳位电平。利用这一点,具有正参考电压的正钳位器电路构造如下。

在正半周期期间,电容器两端的电压和参考电压共同维持输出电压电平。在负半周期期间,当阴极电压小于阳极电压时,二极管导通。这些变化使得输出电压如上图所示。
负钳位器
负钳位电路由二极管、电阻器和电容器组成,它将输出信号移至输入信号的负部分。下图解释了负钳位电路的结构。

在正半周期期间,电容器充电至峰值 $v_{m}$。二极管正向偏置并导通。在负半周期期间,二极管受到反向偏置并开路。此时电路的输出为
$$V_{0}=V_{i}+V_{m}$$
因此,信号被负钳位,如上图所示。输出信号根据输入的变化而变化,但随着输入电压的增加,电平会根据电容器上的电荷而变化。
具有正 V r的负钳位器
负钳位电路如果用某个正参考电压偏置,该电压将被添加到输出以提高钳位电平。利用这一点,具有正参考电压的负钳位器电路构造如下。

尽管输出电压被负钳位,但由于所施加的参考电压为正,所以输出波形的一部分升高至正电平。在正半周期期间,二极管导通,但输出等于所施加的正参考电压。在负半周期期间,二极管表现为开路,电容器两端的电压形成输出。
具有负 V r的负钳位器
负钳位电路如果用一些负参考电压偏置,该电压将被添加到输出以提高钳位电平。利用这一点,具有负参考电压的负钳位器电路构造如下。

二极管的阴极连接有负参考电压,该参考电压小于零电压和阳极电压。因此,二极管在正半周期期间、零电压电平之前开始导通。在负半周期期间,电容器两端的电压出现在输出端。因此,波形被钳位到负部分。
应用领域
Clippers 和 Clampers 有很多应用,例如
剪子
- 用于波形的生成和整形
- 用于保护电路免受尖峰影响
- 用于振幅恢复器
- 用作电压限制器
- 用于电视电路
- 用于调频发射机
夹具
- 用作直流恢复器
- 用于消除扭曲
- 用作电压倍增器
- 用于放大器的保护
- 用作测试设备
- 用作基线稳定剂
限制器和电压倍增器
与削波器和钳位器等波形整形电路一起,二极管还用于构建其他电路,例如限制器和电压倍增器,我们将在本章中讨论这些电路。二极管还有另一个重要的应用,称为整流器,稍后将讨论。
限制器
我们在使用这些限幅器和钳位器时经常遇到的另一个名称是限制器电路。限幅电路可以理解为限制输出电压不超过预定值的电路。
这或多或少是一个限幅电路,不允许信号超过指定值。实际上,削波可以被称为极限程度的限制。因此限制可以理解为平滑限幅。
下图显示了限制器电路的一些示例 -

限幅器电路的性能可以从其传输特性曲线来了解。此类曲线的示例如下。

图表中指定了表示限制器特性的下限和上限。该图的输出电压可以理解为
$$V_{0}= L_{-},KV_{i},L_{+}$$
在哪里
$$L_{-}=V_{i}\leq \frac{L_{-}}{k}$$
$$KV_{i}=\frac{L_{-}}{k}< V_{i}<\frac{L_{+}}{k}$$
$$L_{+}=V_{i}\geq \frac{L_{+}}{K}$$
限制器的类型
限制器有几种类型,例如
单极限制器- 该电路以一种方式限制信号。
双极限制器- 该电路以两种方式限制信号。
软限制器- 即使输入发生微小变化,该电路的输出也可能会发生变化。
硬限幅器- 输出不会轻易随着输入信号的变化而变化。
单限幅器- 该电路采用一个二极管进行限幅。
双限制器- 该电路采用两个二极管进行限制。
电压倍增器
在某些应用中,在某些情况下需要倍增电压。借助使用二极管和电容器的简单电路可以轻松完成此操作。如果电压加倍,这样的电路称为电压倍增器。这可以扩展为三倍电压器或四倍电压器等以获得高直流电压。
为了更好地理解,让我们考虑一个将电压乘以 2 倍的电路。该电路可以称为倍压器。下图所示为倍压器电路。
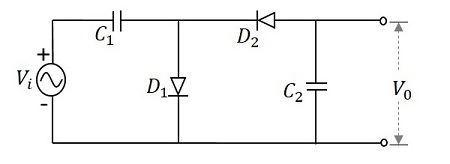
施加的输入电压是正弦波形式的交流信号,如下图所示。

在职的
通过分析输入信号的每个半周期就可以理解电压倍增电路。每个周期使二极管和电容器以不同的方式工作。让我们试着理解这一点。
在第一个正半周期内− 当施加输入信号时,电容器 $C_{1}$ 充电,二极管 $D_{1}$ 正向偏置。虽然二极管 $D_{2}$ 反向偏置,但电容器 $C_{2}$ 没有任何电荷。这使得输出 $V_{0}$ 为 $V_{m}$
这可以从下图来理解。
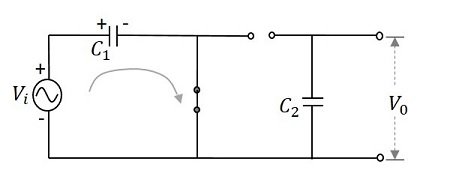
因此,在 0 到 $\pi$ 期间,产生的输出电压将为 $V_{max}$。电容器 $C_{1}$ 通过正向偏置二极管 $D_{1}$ 充电以提供输出,而 $C_{2}$ 不充电。该电压出现在输出端。
在负半周期期间- 此后,当负半周期到来时,二极管 $D_{1}$ 获得反向偏置,二极管 $D_{2}$ 获得正向偏置。二极管 $D_{2}$ 通过电容器 $C_{2}$ 获取电荷,电容器在此过程中充电。然后电流流过电容器 $C_{1}$ 进行放电。从下图可以理解。
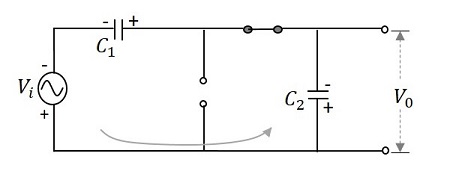
因此,在 $\pi$ 到 $2\pi$ 期间,电容器 $C_{2}$ 两端的电压将为 $V_{max}$。而充满电的电容器$C_{1}$则倾向于放电。现在两个电容器的电压一起出现在输出端,即 $2V_{max}$。因此,该周期内的输出电压$V_{0}$为$2V_{max}$
在下一个正半周期内- 电容器 $C_{1}$ 从电源充电,二极管 $D_{1}$ 获得正向偏置。电容器 $C_{2}$ 保留电荷,因为它找不到放电方式,并且二极管 $D_{2}$ 受到反向偏置。现在,该周期的输出电压 $V_{0}$ 获得两个电容器的电压,它们一起出现在输出端,即 $2V_{max}$。
在下一个负半周期期间- 下一个负半周期使电容器 $C_{1}$ 再次从其完全充电状态放电,并使二极管 $D_{1}$ 反向偏置,而 $D_{2}$ 正向和电容器$C_{2}$ 进一步充电以维持其电压。现在,该周期的输出电压 $V_{0}$ 获得两个电容器的电压,它们一起出现在输出端,即 $2V_{max}$。
因此,输出电压 $V_{0}$ 在整个操作过程中保持为 $2V_{max}$,这使得该电路成为倍压器。
电压倍增器主要用于需要高直流电压的地方。例如,阴极射线管和计算机显示器。
分压器
虽然二极管用于倍增电压,但可以将一组串联电阻制成一个小型网络来分压。这种网络称为分压器网络。
分压器是一种将较大电压变为较小电压的电路。这是使用串联电阻来完成的。输出将是输入的一小部分。输出电压取决于其驱动的负载的电阻。
让我们尝试了解分压器电路的工作原理。下图是一个简单的分压器网络的示例。

如果我们尝试画出输出电压的表达式,
$$V_{i}=i\left ( R_{1}+R_{2} \right )$$
$$i=\frac{V-{i}}{\left ( R_{1}+R_{2} \right )}$$
$$V_{0}=i \:R_{2}\rightarrow \:i\:=\frac{V_{0}}{R_{2}}$$
两者比较,
$$\frac{V_{0}}{R_{2}}=\frac{V_{i}}{\left ( R_1 + R_{2} \right )}$$
$$V_{0}=\frac{V_{i}}{\left ( R_1 + R_{2} \right )}R_{2}$$
这是获取输出电压值的表达式。因此,输出电压根据网络中电阻器的电阻值进行划分。添加更多电阻器以获得不同输出电压的不同分数。
让我们通过一个示例问题来了解有关分压器的更多信息。
例子
计算输入电压为 10v、两个串联电阻 2kΩ 和 5kΩ 的网络的输出电压。

输出电压 $V_{0}$ 由下式给出
$$V_{0}=\frac{V_{i}}{\left ( R_1 + R_{2} \right )}R_{2}$$
$$=\frac{10}{\left ( 2 + 5 \right )k\Omega }5k\Omega$$
$$=\frac{10}{7}\times 5=\frac{50}{7}$$
$$=7.142v$$
上述问题的输出电压$V_0$为7.14v
电子电路 - 二极管作为开关
二极管是一种两端 PN 结,可用于各种应用。此类应用之一是电气开关。PN 结在正向偏置时表现为闭路,在反向偏置时表现为开路。因此,正向和反向偏置状态的变化使二极管起到开关的作用,正向为导通状态,反向为截止状态。

电气开关优于机械开关
由于以下原因,电气开关比机械开关更受青睐 -
- 机械开关容易使金属氧化,而电气开关则不会。
- 机械开关具有可动触点。
- 它们比电气开关更容易受到压力和应变。
- 机械开关的磨损常常会影响其工作。
因此,电气开关比机械开关更有用。