LPF和HPF的特殊功能

低通和高通滤波器电路在许多应用中用作特殊电路。低通滤波器（LPF）可以用作积分器，而高通滤波器（HPF）可以用作微分器。这两个数学函数只有使用这些电路才可能实现，这减少了电子工程师在许多应用中的工作量。

低通滤波器作为积分器

在低频下，容抗趋于无穷大，在高频下，电抗变为零。因此，在低频下，LPF 具有有限输出，而在高频下，输出为零，这对于积分器电路来说是相同的。因此，低通滤波器可以说是作为积分器工作的。

让 LPF 充当积分器

$$\tau \gg T$$

其中$\tau = RC$ 电路的时间常数

那么C上的电压变化就非常小。

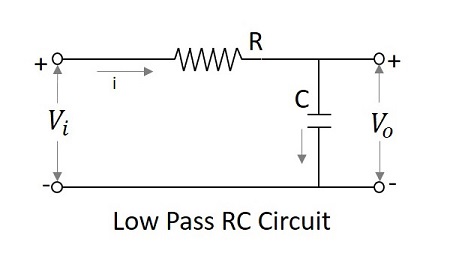
$$V_{i}=iR+\frac{1}{C} \int i \:dt$$

$$V_{i}\cong iR$$

$$自 \:\: \frac{1}{C} \int i \:dt \ll iR$$

$$i=\frac{V_{i}}{R}$$

$$ 自 \:\: V_{0}=\frac{1}{C}\int i dt =\frac{1}{RC}\int V_{i}dt=\frac{1}{\tau } \int V_{i} dt$$

$$输出 \propto \int 输入$$

因此，具有大时间常数的 LPF 产生的输出与输入的积分成正比。

实际低通滤波器用作积分器时的频率响应如下所示。

如果给积分器电路输入正弦波，则输出将为余弦波。如果输入是方波，则输出波形将改变其形状并如下图所示。

在低频下，微分器的输出为零，而在高频下，其输出具有某个有限值。这与微分器相同。因此，高通滤波器被称为微分器。

如果 RC HPF 的时间常数远小于输入信号的时间周期，则电路将充当微分器。那么与 C 上的压降相比，R 上的压降非常小。

$$V_{i}=\frac{1}{C}\int i \:dt +iR$$

但 $iR=V_{0}$ 很小

$$自 V_{i}=\frac{1}{C}\int i \:dt$$

$$i=\frac{V_{0}}{R}$$

$$自 \: V_{i} =\frac{1}{\tau }\int V_{0} \:dt$$

其中$\tau =RC$ 电路的时间常数。

两边微分，

$$\frac{dV_{i}}{dt}=\frac{V_0}{\tau }$$

$$V_{0}=\tau \frac{dV_{i}}{dt}$$

$$自 \:V_{0}\propto \frac{dV_{i}}{dt}$$

输出与输入信号的微分成正比。

实际高通滤波器用作微分器时的频率响应如下所示。

如果微分器电路的输入为正弦波，则输出将为余弦波。如果输入是方波，则输出波形将改变其形状并如下图所示。

这两种电路主要用于各种电子应用中。当施加的输入趋于稳定变化时，微分器电路会产生恒定的输出电压。当施加的输入电压恒定时，积分器电路会产生稳定变化的输出电压。