微波工程 - 测量
正如第一章已经提到的,在微波工程领域中存在许多应用。因此,在使用不同的应用时,我们经常需要测量不同的值,例如功率、衰减、相移、驻波比、阻抗等,以便有效使用。
在本章中,让我们看看不同的测量技术。
功率测量
测量的微波功率是波导中任意位置的平均功率。功率测量可以分为三种类型。
-
低功率测量(0.01mW至10mW)
示例 - 测辐射热技术
-
中等功率(10mW至1W)的测量
示例 - 热量计技术
-
高功率测量(>10W)
示例 - 热量计瓦特计
让我们详细了解一下它们。
低功率测量
微波功率的测量在0.01mW到10mW左右,可以理解为小功率的测量。
辐射热测量计是一种用于低微波功率测量的设备。辐射热测量计中使用的元件可以具有正温度系数或负温度系数。例如,Barrater具有正温度系数,其电阻随着温度的升高而增加。热敏电阻具有负温度系数,其阻值随着温度的升高而减小。
它们中的任何一个都可以在辐射热测量计中使用,但电阻的变化与用于测量的微波功率成正比。该测辐射热计作为一个臂桥使用,因此引起的任何不平衡都会影响输出。使用辐射热测量计的桥式电路的典型示例如下图所示。

这里的毫安表给出了流动的电流值。电池是可变的,当测辐射热计的Behave引起不平衡时,可以改变电池以获得平衡。在直流电池电压中进行的这种调整与微波功率成正比。该电路的功率处理能力是有限的。
中等功率的测量
微波功率的测量在10mW到1W左右,可以理解为中等功率的测量。
采用特殊负载,通常保持一定的比热值。待测量的功率施加在其输入端,这会成比例地改变其已维持的负载的输出温度。温升差异决定了负载的微波输入功率。
这里使用电桥平衡技术来获得输出。传热法用于功率的测量,这是一种量热技术。
高功率测量
微波功率的测量在10W到50KW左右,可以理解为大功率的测量。
高微波功率通常通过量热瓦特计来测量,其可以是干式和流量式的。干式因其使用填充有高磁滞损耗的电介质的同轴电缆而得名,而流动式因其使用水或油或一些对微波有良好吸收剂的液体而得名。
获取液体在进入负载之前和之后的温度变化以用于值的校准。该方法的局限性在于流量确定、校准和热惯性等。
衰减测量
在实践中,微波组件和设备通常会提供一些衰减。所提供的衰减量可以通过两种方式来测量。它们是 - 功率比法和射频替代法。
衰减是输入功率与输出功率的比率,通常以分贝表示。
$$衰减 \: 单位 \: dBs = 10 \: log\frac{P_{in}}{P_{out}}$$
其中 $P_{in}$ = 输入功率,$P_{out}$ = 输出功率
功率比法
在该方法中,衰减的测量分两个步骤进行。
步骤 1 - 整个微波工作台的输入和输出功率是在没有必须计算衰减的设备的情况下完成的。
步骤 2 - 整个微波工作台的输入和输出功率是通过必须计算衰减的设备来完成的。
比较这些功率的比率即可得出衰减值。
下图是解释这一点的两个设置。


缺点- 当输入功率较低且网络衰减较大时,功率和衰减测量可能不准确。
射频替代法
在该方法中,衰减的测量分三个步骤进行。
步骤 1 - 使用必须计算衰减的网络测量整个微波工作台的输出功率。
步骤 2 - 通过用精密校准的衰减器替换网络来测量整个微波工作台的输出功率。
步骤 3 - 现在,调整该衰减器以获得与网络测量的相同功率。
下图是解释这一点的两个设置。

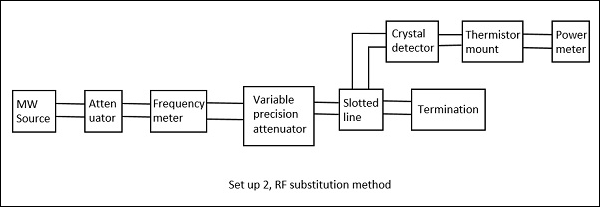
衰减器上的调整值直接给出网络的衰减。这里避免了上述方法的缺点,因此这是测量衰减的更好程序。
相移测量
在实际工作条件下,信号与实际信号可能会发生相位变化。为了测量这种相移,我们使用比较技术来校准相移。
计算相移的设置如下图所示。
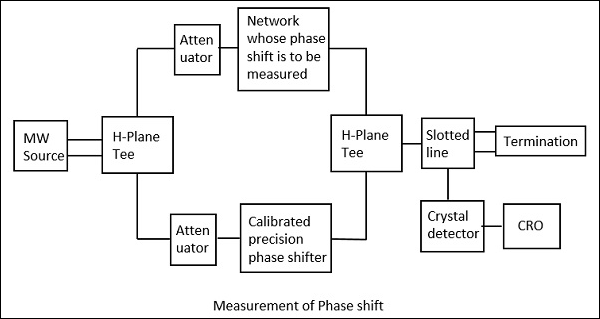
这里,微波源产生信号后,通过H平面T形接头,其中一个端口连接到要测量相移的网络,另一个端口连接到可调精密移相器。
解调输出是 1 KHz 正弦波,可在连接的 CRO 中观察到。对该移相器进行调整,使得其1KHz正弦波的输出也与上述匹配。通过在双模式 CRO 中观察完成匹配后,该精密移相器为我们提供相移读数。通过下图可以清楚地理解这一点。

该过程是相移测量中最常用的一种。现在,让我们看看如何计算 VSWR。
驻波比测量
在任何微波实际应用中,任何类型的阻抗失配都会导致驻波的形成。这些驻波的强度通过电压驻波比 ($VSWR$) 来测量。最大电压与最小电压之比即为$VSWR$,用$S$ 表示。
$$S = \frac{V_{max}}{V_{min}} = \frac{1+\rho }{1-\rho}$$
其中,$\rho = 反射 \: 效率 = \frac{P_{reflected}}{P_{incident}}$
$VSWR$ 的测量可以通过两种方式完成:低 $VSWR$ 测量和高 $VSWR$ 测量。
低驻波比 (S <10) 的测量
低电压驻波比的测量可以通过调节衰减器在直流毫伏表上获得读数来完成,即驻波比表。可以通过调节槽线和衰减器来获取读数,使直流毫伏表显示满量程读数和最小读数。
现在计算这两个读数即可找出网络的 $VSWR$。
高驻波比测量 (S>10)
大于10的高VSWR$的测量可以通过称为双极小值法的方法来测量。在该方法中,取最小值处的读数,并且还取前波峰和后波峰中最小值半点处的读数。这可以通过下图来理解。
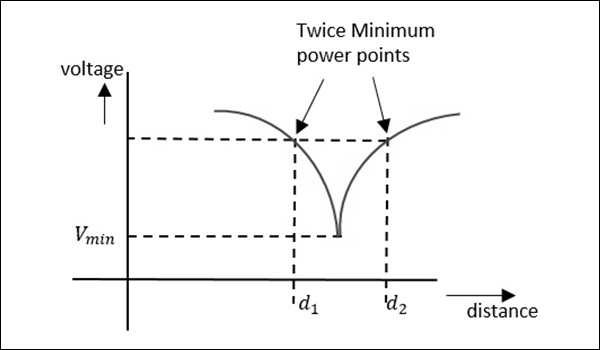
现在,$VSWR$ 可以通过关系计算,如下所示:
$$VSWR = \frac{\lambda_{g}}{\pi(d_2-d_1)}$$
其中,$\lambda_g \: 是\: 引导\: 波长$
$$\lambda_g = \frac{\lambda_0}{\sqrt{1-(\frac{\lambda_0}{\lambda_c})^2}} \quad 其中 \: \lambda_0 \: = {c}/{f} $$
由于这里考虑的是两个最小值点,因此称为双极小值法。下面我们就来了解一下阻抗的测量。
阻抗测量
除了Magic Tee之外,我们还有两种不同的方法,一种是使用槽线,另一种是使用反射计。
使用槽线的阻抗
在此方法中,使用开槽线和负载 $Z_L$ 测量阻抗,并使用此方法可以确定 $V_{max}$ 和 $V_{min}$。在该方法中,阻抗的测量分两个步骤进行。
步骤 1 - 使用负载 $Z_L$ 确定 Vmin。
步骤 2 - 通过短路负载确定 Vmin。
如下图所示。


当我们尝试使用负载获取 $V_{max}$ 和 $V_{min}$ 的值时,我们会得到某些值。然而,如果通过短路负载来完成同样的操作,则最小值会向右或向左移动。如果该偏移向左,则意味着负载是感性负载,如果向右偏移,则意味着负载本质上是电容性负载。下图解释了这一点。

通过记录数据,可以计算出未知的阻抗。阻抗和反射系数$\rho$可以在幅度和相位上获得。
使用反射计测量阻抗
与槽线不同,反射计仅有助于找到阻抗的大小,而不是相位角。在该方法中,采用两个相同但方向不同的定向耦合器。
这两个耦合器用于对来自负载的入射功率 $P_i$ 和反射功率 $P_r$ 进行采样。反射计的连接如下图所示。用于获取反射系数$\rho$的大小,由此可以得到阻抗。

根据反射计的读数,我们有
$$\rho = \sqrt{\frac{P_r}{P_i}}$$
根据 $\rho$ 的值,可以计算出 $VSWR$(即 $S$)和阻抗:
$$S = \frac{1+\rho}{1-\rho} \quad 和 \quad \frac{z-z_g}{z+z_g} = \rho$$
其中,$z_g$为已知波阻抗,$z$为未知阻抗。
虽然这里观察到了正向和反向波参数,但由于耦合器的方向性,不会产生干扰。衰减器有助于保持低输入功率。
空腔谐振器Q值的测量
虽然测量空腔谐振器Q值的方法有传输法、阻抗法和瞬态衰减或减量法三种,但最简单和最常用的方法是传输法。因此,让我们看一下它的测量设置。

在该方法中,空腔谐振器充当传输装置。输出信号被绘制为频率的函数,从而产生如下图所示的谐振曲线。

根据上述设置,改变微波源的信号频率,保持信号电平恒定,然后测量输出功率。将空腔谐振器调谐到该频率,并再次记录信号电平和输出功率以注意到差异。
当绘制输出时,就得到了谐振曲线,从中我们可以注意到半功率带宽 (HPBW) $(2 \Delta)$ 值。
$$2\Delta = \pm \frac{1}{Q_L}$$
其中,$Q_L$是加载的值
$$或 \quad Q_L = \pm \frac{1}{2\Delta} = \pm \frac{w}{2(w-w_0)}$$
如果忽略微波源与腔体之间的耦合以及探测器与腔体之间的耦合,则
$$Q_L = Q_0 \:(已卸载\: Q)$$
退税
该系统的主要缺点是,由于工作频带较窄,在 Q 值非常高的系统中精度稍差。
我们已经介绍了多种不同参数的测量技术。现在,让我们尝试解决一些关于这些的示例问题。
