微波工程 - 快速指南
微波工程 - 简介
电磁频谱由整个电磁辐射范围组成。辐射是在传播时传播和扩散的能量。形成电磁频谱的电磁辐射类型如下面的屏幕截图所示。

现在让我们来看看微波的特性。
微波的特性
以下是微波的主要特性。
微波是发射波长较短的电磁能的波。
微波不会被电离层反射。
微波沿直线传播并被传导表面反射。
微波在较短距离内很容易衰减。
微波电流可以流过电缆的薄层。
微波炉的优点
微波有很多优点,例如:
支持更大的带宽,从而传输更多的信息。因此,微波用于点对点通信。
更大的天线增益是可能的。
带宽越大,传输的数据速率就越高。
随着频率更高,天线尺寸会减小。
由于信号频率较高,功耗较低。
通过使用视线传播来减少衰落的影响。
在雷达系统中提供有效的反射区域。
高容量的卫星和地面通信是可能的。
可以开发低成本的微型微波元件。
在所有可用的操作频率范围内有效地利用频谱,实现各种应用。
微波炉的缺点
微波炉有一些缺点,例如:
- 设备成本或安装成本较高。
- 它们很重并且占据更多的空间。
- 可能会发生电磁干扰。
- 介电性能可能会随温度变化。
- 电力固有的低效率。
微波的应用
微波有各种各样的应用,这是其他辐射所不可能的。他们是 -
无线通讯
- 对于长途电话
- 蓝牙
- WIMAX运营
- 户外广播传输
- 广播辅助服务
- 远程拾取装置
- 工作室/发射机链接
- 直播卫星 (DBS)
- 个人通信系统 (PCS)
- 无线局域网 (WLAN)
- 蜂窝视频 (CV) 系统
- 汽车防撞系统
电子产品
- 快速无抖动开关
- 移相器
- 高频产生
- 调整元件
- ECM/ECCM(电子对抗)系统
- 扩频系统
商业用途
- 防盗警报器
- 车库开门器
- 警用测速仪
- 非接触式识别
- 手机、寻呼机、无线 LAN
- 卫星电视、XM 广播
- 运动探测器
- 遥感
导航
- 全球导航卫星系统
- 全球定位系统(GPS)
军事和雷达
雷达探测目标的范围和速度。
声纳应用
空中管制
天气预报
船舶航行
扫雷应用
限速执法
军事用途微波频率用于通信和上述应用。
研究应用
- Atomics共振
- 核共振
射电天文学
- 标记宇宙微波背景辐射
- 探测宇宙中的强大波
- 探测宇宙和地球大气层中的许多辐射
食品工业
- 用于重新加热和烹饪的微波炉
- 食品加工应用
- 预热应用
- 预煮
- 烘烤谷物/豆类
- 烘干薯片
- 水分均化
- 吸收水分子
工业用途
- 硫化橡胶
- 分析化学应用
- 干燥和反应过程
- 加工陶瓷
- 聚合物基体
- 表面改性
- 化学气相处理
- 粉体加工
- 药品灭菌
- 化学合成
- 废物整治
- 电力传输
- 隧道掘进
- 破碎岩石/混凝土
- 破碎煤层
- 水泥养护
- 射频照明
- 聚变反应堆
- 主动拒绝系统
半导体加工技术
- 反应离子蚀刻
- 化学气相沉积
光谱学
- 电子顺磁共振(EPR 或 ESR)光谱
- 了解化学物质中的不成对电子
- 了解材料中的自由基
- 电子化学
医疗应用
- 监测心跳
- 肺水检测
- 肿瘤检测
- 局部高热
- 治疗应用
- 局部供暖
- 血管成形术
- 微波断层扫描
- 微波声学成像
任何波的传播都需要介质。不同类型的传输线用于传播微波。让我们在下一章中了解它们。
微波工程 - 传输线
传输线是一种将能量从一点传输到另一点的连接器。输电线路理论的研究有助于电力和设备的有效利用。
传输线基本上有四种类型 -
- 两线并行传输线
- 同轴线
- 带状基板传输线
- 波导
在发射或接收时,必须有效地进行能量传输,而不浪费电力。为了实现这一目标,必须考虑某些重要参数。
输电线路主要参数
传输线的重要参数是电阻、电感、电容和电导。
电阻和电感一起称为传输线阻抗。
电容和电导一起称为导纳。
反抗
制造传输线的材料所提供的电阻将是相当大的,特别是对于较短的传输线。随着线路电流的增加,欧姆损耗 $\left ( I^{2}R \: loss \right )$ 也会增加。
长度为“$l$”、横截面为“$a$”的导体的电阻$ R$表示为
$$R = \rho \frac{l}{a}$$
在哪里
$\rho$ = 导体材料的电阻率,为常数。
温度和电流频率是影响线路电阻的主要因素。导体的电阻随温度的变化而线性变化。然而,如果电流频率增加,则流向导体表面的电流密度也会增加。否则,朝向导体中心的电流密度会增加。
这意味着,流向导体表面的电流较多,流向中心的电流较少,这称为集肤效应。
电感
在交流输电线路中,电流呈正弦波流动。该电流感应出一个垂直于电场的磁场,该磁场也呈正弦变化。这就是众所周知的法拉第定律。这些字段如下图所示。

这种变化的磁场会在导体中感应出一些电动势。现在,该感应电压或电动势沿与最初流动的电流相反的方向流动。沿相反方向流动的电动势等效地由称为电感的参数表示,该参数是抵抗电流移动的属性。
它由“ L ”表示。测量单位是“亨利(H) ”。
电导
输电线路与地之间以及相导体之间都会存在漏电流。这种少量的漏电流通常流过绝缘体的表面。该漏电流的倒数称为电导。它由“ G ”表示。
线电流的流动与电感相关,两点之间的电压差与电容相关。电感与磁场相关,而电容与电场相关。
电容
相导体之间的电压差在导体之间产生电场。两个导体就像平行板,它们之间的空气变成电介质。这种模式会在导体之间产生电容效应。
特性阻抗
如果考虑均匀无损传输线,对于沿一个方向传播的波,沿该传输线(没有反射)的电压和电流的幅值之比称为特性阻抗。
它用$Z_0$表示
$$Z_0 = \sqrt{\frac{电压\:\: 波\:\: 值}{电流\:\: 波\:\: 值}}$$
$$Z_0 = \sqrt{\frac{R + jwL}{G + jwC}}$$
对于无损线,$R_0 = \sqrt{\frac{L}{C}}$
其中$L$ 和$C$ 是每单位长度的电感和电容。
阻抗匹配
为了实现向负载传输最大功率,必须进行阻抗匹配。为了实现这种阻抗匹配,需要满足以下条件。
负载的电阻应等于源的电阻。
$$R_L = R_S$$
负载的电抗应等于源的电抗,但符号相反。
$$X_L = -X_S$$
这意味着,如果源是感性的,则负载应该是容性的,反之亦然。
反射系数
表示由于传输线阻抗不匹配而反射的能量大小的参数称为反射系数。它由 $\rho$ (rho)表示。
它可以定义为“负载端反射电压与入射电压之比”。
$$\rho = \frac{反射电压}{入射电压} = \frac{V_r}{V_i} \: 负载\: 端子$$
如果设备和传输线之间的阻抗彼此不匹配,则能量会被反射。反射的能量越高,$\rho$ 反射系数的值就越大。
电压驻波比 (VSWR)
当入射波被反射时形成驻波。形成的驻波包含一些电压。驻波的幅度可以用驻波比来测量。
驻波中最大电压与最小电压之比可定义为电压驻波比(VSWR)。它由“$S$”表示。
$$S = \frac{\left |V_{max} \right |}{\left |V_{min} \right |} \quad 1\:\leq S \leq \infty$$
VSWR 描述了由于入射波和反射波的相位相加和相减而出现在传输线中的电压驻波模式。
因此,它也可以写成
$$S = \frac{1 + \rho }{1 - \rho }$$
阻抗失配越大,驻波的幅度就越高。因此,如果阻抗完美匹配,
$$V_{最大值} : V_{最小值} = 1:1$$
因此,VSWR 的值为 1,这意味着传输是完美的。
输电线路的效率
传输线的效率定义为输出功率与输入功率的比率。
$\% \: 传输线路 \: 的效率 \: \eta = \frac{在接收处传送的功率 \: 从传输 \: 发送的功率 \:结束} \乘以100$
电压调节
电压调整率定义为传输线发送端和接收端之间电压幅值的变化。
$\%\:电压\:调节=\frac{发送\:结束\:电压-\:接收\:结束\:电压}{发送\:结束\:电压} \times 100$
阻抗不匹配造成的损失
如果传输线路没有匹配负载,就会产生损耗。这些损耗有很多类型,如衰减损耗、反射损耗、传输损耗、回波损耗、插入损耗等。
衰减损耗
由于信号在传输线路中被吸收而产生的损耗称为衰减损耗,其表示为
$$衰减 \: 损耗 (dB) = 10 \: log_{10} \left [ \frac{E_i - E_r}{E_t} \right ]$$
在哪里
$E_i$ = 输入能量
$E_r$ = 从负载到输入的反射能量
$E_t$ = 传输至负载的能量
反射损耗
由于传输线阻抗不匹配而导致信号反射而产生的损耗称为反射损耗,其表示为
$$反射 \: 损耗 (dB) = 10 \: log_{10} \left [ \frac{E_i}{E_i - E_r} \right ]$$
在哪里
$E_i$ = 输入能量
$E_r$ = 来自负载的反射能量
传输损耗
通过传输线传输时发生的损耗称为传输损耗,其表示为
$$传输 \: 损耗(dB) = 10 \: log_{10} \: \frac{E_i}{E_t}$$
在哪里
$E_i$ = 输入能量
$E_t$ = 传输的能量
回波损耗
传输线反射功率的度量称为回波损耗,表示为
$$返回 \: 损失(dB) = 10 \: log_{10} \: \frac{E_i}{E_r}$$
在哪里
$E_i$ = 输入能量
$E_r$ = 反射能量
插入损耗
与不使用传输线的能量传输相比,由于使用传输线进行能量传输而产生的损耗称为插入损耗,表示为
$$插入 \: 损耗(dB) = 10 \: log_{10} \: \frac{E_1}{E_2}$$
在哪里
$E_1$ = 直接连接到电源(无需传输线)时负载接收到的能量。
$E_2$ = 当传输线连接在负载和电源之间时负载接收到的能量。
存根匹配
如果负载阻抗与源阻抗不匹配,有时会使用称为“存根匹配”的方法来实现匹配。
将分流器中称为短截线的开路或短路线路部分与主线在某个点或多个点连接的过程可以称为短截线匹配。
在较高的微波频率下,基本上采用两种短截线匹配技术。
单存根匹配
在单短截线匹配中,将具有一定固定长度的短截线放置在距负载一定距离处。它仅用于固定频率,因为对于频率的任何变化,短截线的位置都必须改变,但没有这样做。此方法不适用于同轴线。
双存根匹配
在双螺柱匹配中,两个可变长度的螺柱固定在某些位置。当负载变化时,仅调整短截线的长度即可实现匹配。这作为单频匹配装置广泛应用于实验室实践。
下图显示了存根匹配的外观。

如上图所示,在传输线中进行单短截线匹配和双短截线匹配,以实现阻抗匹配。
传播方式
波同时具有电场和磁场。电场和磁场的所有横向分量均由 z 方向上电场和磁场的轴向分量确定。这允许形成模式,例如微波中的 TE、TM、TEM 和混合模式。让我们看一下模式的类型。
沿三个相互垂直的方向x、y、z的电场和磁场分量的方向如下图所示。

模式类型
微波的传播模式是 -
TEM(横向电磁波)
在这种模式下,电场和磁场都完全垂直于传播方向。$'Z'$ 方向没有组件。
$$E_z = 0 \: 和 \: H_z = 0$$
TE(横向电波)
在这种模式下,电场完全垂直于传播方向,而磁场则不是。
$$E_z = 0 \: 和 \: H_z \ne 0$$
TM(横磁波)
在这种模式下,磁场完全垂直于传播方向,而电场则不是。
$$E_z \ne 0 \: 和 \: H_z = 0$$
HE(混合波)
在这种模式下,电场和磁场都不是纯粹横向于传播方向的。
$$E_z \ne 0 \: 和 \: H_z \ne 0$$
多导体线路通常支持 TEM 传播模式,因为传输线理论仅适用于具有去路和返回路径的导体系统,即能够支持 TEM 波的导体系统。
波导是单导线,允许 TE 和 TM 模式,但不允许 TEM 模式。开放式导体导轨支持混合波。传输线的类型将在下一章讨论。
传输线的类型
传统的明线传输线不适合微波传输,因为辐射损耗很高。在微波频率下,所使用的传输线可大致分为三种类型。他们是 -
- 多导线
- 同轴线
- 带状线
- 微带线
- 槽线
- 共面线等
- 单导线(波导)
- 矩形波导
- 圆形波导
- 椭圆波导
- 单脊波导
- 双脊波导等
- 开放边界结构
- 介电棒
- 开放式波导等
多导线
具有多于一根导体的传输线称为多导体线。
同轴线
该产品主要用于高频应用。
同轴线由内径为d的内导体和围绕它的同心圆柱形绝缘材料组成。它被外导体包围,外导体是一个内径为D的同心圆柱体。通过查看下图就可以很好地理解该结构。

同轴电缆的基本模式和主导模式是 TEM 模式。同轴电缆中没有截止频率。它通过所有频率。然而,对于更高的频率,一些高阶非 TEM 模式开始传播,导致大量衰减。
带状线
这些是平面传输线,使用频率为 100MHz 至 100GHz。
带状线由宽度为ω的中心薄导电带组成,其宽度大于其厚度t。它放置在两个宽接地板之间厚度为 b/2 的低损耗电介质 (ε r ) 基板内。接地板的宽度比板之间的间距大五倍。
金属中心导体的厚度和金属接地层的厚度相同。下图为带状线结构的剖面图。

带状线的基本模式和主导模式是 TEM 模式。对于b<λ/2,横向上不会有传播。带状线的阻抗与内导体的宽度ω与接地层之间的距离b的比率成反比。
微带线
带状线的缺点是无法进行调整和调谐。微带线可以避免这种情况,微带线允许安装有源或无源器件,并且还允许在电路制造后进行细微调整。
微带线是一种不对称的平行板传输线,具有底部金属化接地的介电基板和顶部厚度为“t”、宽度为“ω”的薄导电带。通过查看下图即可理解这一点,该图显示了微带线。

微带线的特性阻抗是带线宽度(ω)、厚度(t)以及线与接地平面之间的距离(h)的函数。微带线有多种类型,如嵌入式微带线、倒置微带线、悬置微带线和开槽微带线等。
除此之外,其他一些TEM线如平行带状线和共面带状线也已用于微波集成电路。
其他线路
平行带状线类似于两导体传输线。可支持准TEM模式。下图解释了这一点。

共面带状线由两条导电带组成,其中一条接地,两者放置在同一基板表面上,以方便连接。下图解释了这一点。

槽线传输线由介电基板上的导电涂层中的槽或间隙组成,其制造过程与微带线相同。以下是其图解表示。

共面波导由沉积在电介质板表面上的一条金属薄膜组成。该板具有两个电极,两个电极邻近并平行于带材延伸到同一表面上。下图解释了这一点。

所有这些微带线都用于微波应用,其中使用体积大且制造成本昂贵的传输线将是一个缺点。
开放边界结构
这些也可以称为开放电磁波导。未完全封闭在金属屏蔽中的波导可以被视为开放式波导。自由空间也被认为是一种开放波导。
开放波导可以定义为具有纵向轴对称性和无界横截面、能够引导电磁波的任何物理装置。它们拥有一个不再离散的频谱。微带线和光纤也是开放波导的例子。
微波工程 - 波导
一般来说,如果信号或特定频带信号的频率较高,则带宽利用率较高,因为该信号为其他信号提供了更多的累积空间。然而,高频信号无法在不衰减的情况下传播更远的距离。我们研究了传输线有助于信号传输更远的距离。
微波通过微波电路、组件和设备传播,这些电路、组件和设备充当微波传输线的一部分,广泛称为波导。
具有均匀横截面的中空金属管,通过管内壁的连续反射来传输电磁波,称为波导。
下图显示了波导的示例。

在微波通信中通常优选波导。波导是传输线的一种特殊形式,是一种空心金属管。与传输线不同,波导没有中心导体。
波导的主要特点是 -
管壁提供分布电感。
管壁之间的空白空间提供分布电容。
这些体积庞大且昂贵。
波导的优点
以下是波导的一些优点。
波导易于制造。
它们可以处理非常大的功率(以千瓦为单位)。
波导中的功率损耗可以忽略不计。
它们的损耗非常低(α 衰减值低)。
当微波能量通过波导传播时,其损耗比同轴电缆要低。
波导的类型
有五种类型的波导。
- 矩形波导
- 圆形波导
- 椭圆波导
- 单脊波导
- 双脊波导
下图显示了波导的类型。
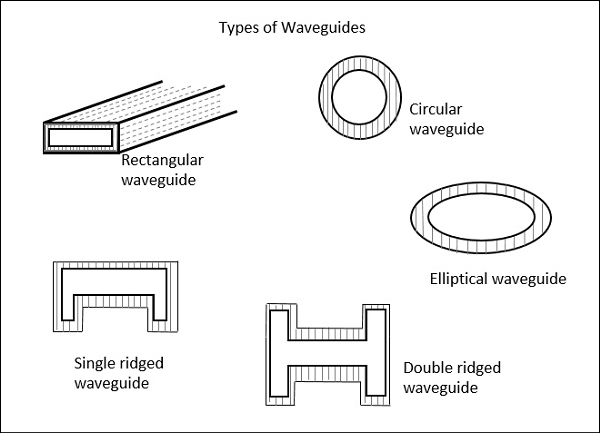
上面显示的波导类型是中心空心的,由铜壁组成。它们的内表面有一层薄薄的金或银衬里。
现在让我们比较一下传输线和波导。
传输线与波导
传输线和波导之间的主要区别是 -
可以支持 TEM 波的两导体结构是传输线。
能够支持TE波或TM波但不能支持TEM波的单导体结构称为波导。
下表列出了传输线和波导之间的差异。
| 传输线 | 波导 |
|---|---|
| 支持TEM波 | 不支持TEM波 |
| 所有频率均可通过 | 只有大于截止频率的频率才能通过 |
| 两导体传输 | 一根导线传输 |
| 反射较少 | 波通过波导壁的反射传播 |
| 它具有特性阻抗 | 它具有波阻抗 |
| 波的传播是根据“电路理论” | 波的传播是根据“场论” |
| 它有一个接地回路导体 | 不需要返回导体,因为波导主体充当大地 |
| 带宽不受限制 | 带宽有限 |
| 波浪不散 | 波浪被分散 |
相速度
相速度是波改变相位以经历2π弧度相移的速率。它可以理解为正弦波的波分量在调制时的速度变化。
让我们推导出相速度的方程。
根据定义,需要考虑2π弧度处的相位变化率。
这意味着$λ$ / $T$因此,
$$V = \frac{\lambda }{T}$$
在哪里,
$λ$ = 波长,$T$ = 时间
$$V = \frac{\lambda }{T} = \lambda f$$
由于 $f = \frac{1}{T}$
如果我们将分子和分母乘以2π那么,我们有
$$V = \lambda f = \frac{2\pi \lambda f}{2\pi }$$
我们知道 $\omega = 2\pi f$和$\beta = \frac{2\pi }{f}$
上面的方程可以写成,
$$V = \frac{2\pi f}{\frac{2\pi }{\lambda }} = \frac{\omega }{\beta }$$
因此,相速度的方程表示为
$$V_p = \frac{\omega }{\beta }$$
群速度
群速度可以定义为波通过波导传播的速率。这可以理解为调制包络与单独载波相比的传播速率。该调制波穿过波导。
群速度方程表示为
$$V_g = \frac{d\omega }{d\beta }$$
调制包络的速度通常比载波信号慢。
微波工程 - 组件
在本章中,我们将讨论微波元件,例如微波晶体管和不同类型的二极管。
微波晶体管
需要开发特殊的晶体管来承受微波频率。因此,对于微波应用,已经开发出能够在微波频率下提供足够功率的硅npn晶体管。它们的典型功率为 5 瓦,频率为 3GHz,增益为 5dB。下图显示了这种晶体管的截面图。
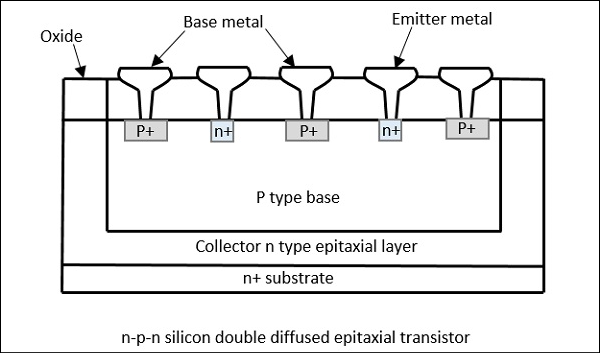
微波晶体管的构造
在构成集电极的n+基板上生长n型外延层。在该n区域上,热生长SiO2层。p基极和重掺杂n发射极扩散到基极中。在氧化物中制作用于欧姆接触的开口。连接是并行进行的。
此类晶体管具有分类为叉指型、覆盖型或矩阵型的表面几何形状。这些形式如下图所示。
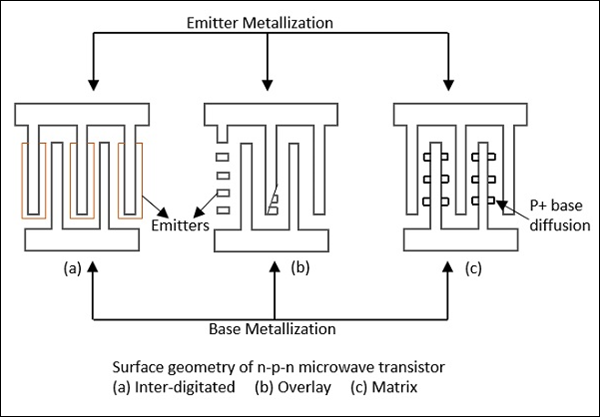
功率晶体管采用所有三种表面几何形状。
小信号晶体管采用叉指表面几何形状。叉指结构适用于 L、S 和 C 频段的小信号应用。
矩阵几何形状有时称为网格或发射器网格。覆盖层和矩阵结构可用作 UHF 和 VHF 区域的功率器件。
微波晶体管的操作
在微波晶体管中,最初发射极-基极和集电极-基极结是反向偏置的。在施加微波信号时,发射极-基极结变得正向偏置。如果考虑pnp晶体管,则应用信号的正峰值,使发射极-基极结正向偏置,使空穴漂移到薄的负基极。空穴进一步加速到集电极和基极端子之间的偏置电压的负端子。连接在集电极上的负载接收电流脉冲。
固态器件
固态微波器件的分类可以完成 -
取决于它们的电气Behave
-
非线性电阻型。
示例 - 压敏电阻(可变电阻)
-
非线性电抗型。
示例 - 变容二极管(可变电抗器)
-
负阻型。
示例 - 隧道二极管、Impatt 二极管、耿氏二极管
-
可控阻抗型。
示例 - PIN 二极管
-
- 取决于它们的构造
- 点接触二极管
- 肖特基势垒二极管
- 金属氧化物半导体器件 (MOS)
- 金属绝缘装置
我们这里提到的二极管类型有很多用途,例如放大、检测、发电、移相、下变频、上变频、限幅调制、开关等。
变容二极管
反向偏置结的电压可变电容可称为变容二极管。变容二极管是一种半导体器件,其中结电容可以根据二极管的反向偏压而变化。典型变容二极管的CV特性及其符号如下图所示。
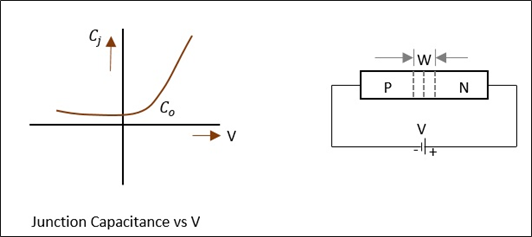
结电容取决于所施加的电压和结设计。我们知道,
$$C_j \: \alpha \: V_{r}^{-n}$$
在哪里
$C_j$ = 结电容
$V_r$ = 反向偏置电压
$n$ = 决定连接类型的参数
如果结是反向偏置的,则移动载流子会耗尽结,从而产生一些电容,其中二极管充当电容器,而结充当电介质。电容随着反向偏压的增加而减小。
二极管的封装包含连接到半导体晶片的电引线和连接到陶瓷外壳的引线。下图显示了微波变容二极管的外观。
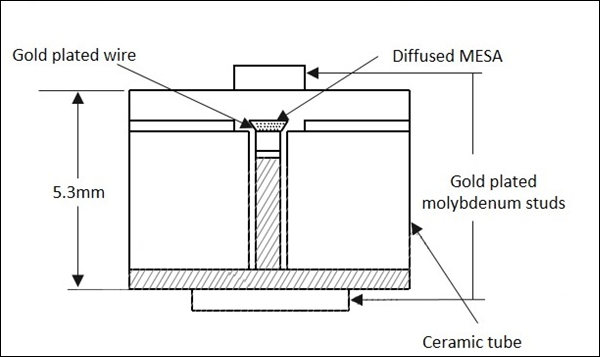
它们能够处理大功率和大反向击穿电压。这些噪音低。尽管结电容的变化是该二极管的一个重要因素,但寄生电阻、电容和电导与每个实际二极管相关,应保持较低。
变容二极管的应用
变容二极管用于以下应用 -
- 上变频
- 参量放大器
- 脉冲产生
- 脉冲整形
- 开关电路
- 微波信号的调制
肖特基势垒二极管
这是一个表现出非线性阻抗的简单二极管。这些二极管主要用于微波检测和混合。
肖特基势垒二极管的构造
半导体颗粒安装在金属底座上。弹簧加载线通过尖点连接到该硅颗粒。它可以轻松安装到同轴或波导线路中。下图给出了一个清晰的构造图。
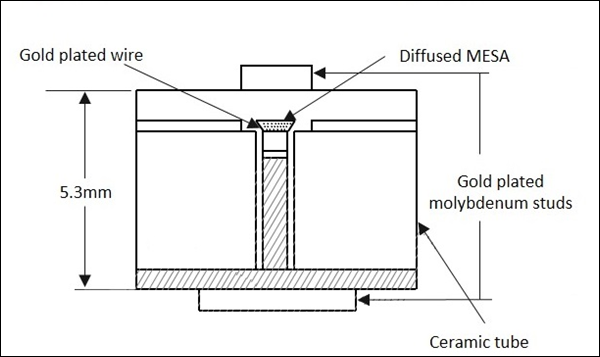
肖特基势垒二极管的操作
随着半导体和金属之间的接触,形成耗尽区。相对而言,金属区具有较小的耗尽宽度。当接触时,电子从半导体流向金属。这种耗尽会在半导体中形成正空间电荷,并且电场会阻碍进一步的流动,从而导致在界面处形成势垒。
在正向偏压期间,势垒高度降低,电子注入到金属中,而在反向偏压期间,势垒高度增加,电子注入几乎停止。
肖特基势垒二极管的优点
这些是以下优点。
- 低成本
- 简单
- 可靠的
- 噪声系数 4 至 5dB
肖特基势垒二极管的应用
这些是以下应用程序。
- 低噪音搅拌机
- 连续波雷达中的平衡混频器
- 微波探测器
耿氏效应装置
JB Gunn 发现当施加的电压超过某个临界值时,流过n 型 GaAs样品的电流会出现周期性波动。在这些二极管中,导带中有两个谷,即L 谷和 U 谷,电子转移发生在它们之间,具体取决于所施加的电场。这种从 L 谷下部到 U 谷上部的粒子数反转效应称为转移电子效应,因此这些被称为转移电子器件(TED)。
耿氏二极管的应用
耿氏二极管广泛用于以下设备 -
- 雷达发射机
- 空中交通管制中的应答器
- 工业遥测系统
- 功率振荡器
- 逻辑电路
- 宽带线性放大器
雪崩渡越时间装置
电压和电流之间存在延迟、雪崩以及传输时间穿过材料的过程被称为负电阻。有助于使二极管表现出这种特性的器件称为雪崩渡越时间器件。
此类器件的示例包括 IMPATT、TRAPATT 和 BARITT 二极管。让我们详细看看它们中的每一个。
冲击二极管
这是一种高功率半导体二极管,用于高频微波应用。IMPATT 的完整形式是IMPact 电离雪崩渡越时间二极管。
当施加到 IMPATT 二极管时,电压梯度会产生高电流。普通二极管最终会因此被击穿。然而,IMPATT 二极管的开发就是为了承受这一切。施加高电势梯度以反向偏置二极管,因此少数载流子流过结。
如果施加射频交流电压叠加在高直流电压上,则空穴和电子的速度增加,通过碰撞电离将它们从晶体结构中击出,从而产生额外的空穴和电子。如果施加的原始直流场处于发展这种情况的阈值,那么它会导致雪崩电流倍增,并且该过程会继续下去。这可以通过下图来理解。

由于这种效应,电流脉冲发生 90° 的相移。然而,由于施加反向偏压,它并没有在那里,而是向阴极移动。脉冲到达阴极所需的时间取决于n+层的厚度,调整该厚度以使其相移 90°。现在,动态射频负电阻被证明存在。因此,IMPATT 二极管既充当振荡器又充当放大器。
下图显示了 IMPATT 二极管的结构细节。

IMPATT 二极管的效率表示为
$$\eta = \left [ \frac{P_{ac}}{P_{dc}} \right ] = \frac{V_a}{V_d}\left [ \frac{I_a}{I_d} \right ]$$
在哪里,
$P_{ac}$ = 交流电源
$P_{dc}$ = 直流电源
$V_a \: \& \: I_a$ = 交流电压和电流
$V_d \: \& \: I_d$ = 直流电压和电流
缺点
以下是 IMPATT 二极管的缺点。
- 它很吵,因为雪崩是一个吵闹的过程
- 调谐范围不如耿氏二极管那么好
应用领域
以下是IMPATT二极管的应用。
- 微波振荡器
- 微波发生器
- 调制输出振荡器
- 接收器本地振荡器
- 负阻放大
- 入侵报警网络(高 Q IMPATT)
- 警用雷达(高Q IMPATT)
- 低功率微波发射器(高Q IMPATT)
- FM 电信发射机(低 Q IMPATT)
- CW 多普勒雷达发射机(低 Q IMPATT)
特拉帕二极管
TRAPATT 二极管的完整形式是捕获等离子体雪崩触发传输二极管。工作频率为数百 MHz 至 GHz 的微波发生器。这些是高峰值功率二极管,通常为n+- p-p+或p+-n-n+结构,具有 n 型耗尽区,宽度从 2.5 到 1.25 µm 不等。下图描述了这一点。

被捕获在该区域后面的低场区域中的电子和空穴被用来填充二极管中的耗尽区。这是通过通过二极管传播的高场雪崩区域来完成的。
下图所示为曲线图,其中AB表示充电,BC表示血浆形成,DE表示血浆提取,EF表示残留提取,FG表示充电。
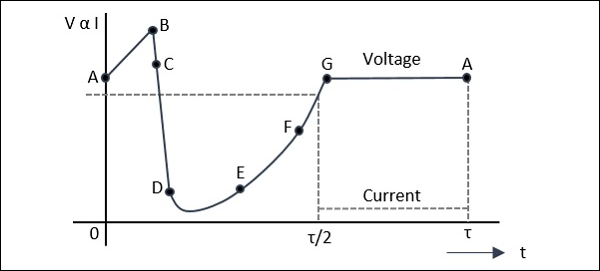
让我们看看每个点会发生什么。
A: A点的电压不足以发生雪崩击穿。在 A 处,由于热生成而产生的电荷载流子导致二极管充电,就像线性电容一样。
AB:此时,电场强度增大。当产生足够数量的载流子时,整个耗尽区的电场减弱,导致电压从 B 降低到 C。
C:这种电荷有助于雪崩继续,并产生电子和空穴的致密等离子体。场进一步减弱,以免电子或空穴离开耗尽层,并捕获剩余的等离子体。
D:在D点电压降低。由于等离子体总电荷与外部电流中每单位时间的电荷相比较大,所以需要很长时间来清除等离子体。
E:在E点,等离子体被去除。空穴和电子的残余电荷分别保留在偏转层的一端。
E 至 F:随着残余电荷的去除,电压增加。
F:在F点,内部产生的所有电荷被移除。
F 到 G:二极管像电容器一样充电。
G:在G点,二极管电流在半个周期内为零。电压保持恒定,如上图所示。这种状态一直持续到电流恢复并重复该循环。
雪崩区速度 $V_s$ 表示为
$$V_s = \frac{dx}{dt} = \frac{J}{qN_A}$$
在哪里
$J$ = 电流密度
$q$ = 电子电荷 1.6 x 10 -19
$N_A$ = 掺杂浓度
雪崩区将快速扫过二极管的大部分,载流子的渡越时间表示为
$$\tau_s = \frac{L}{V_s}$$
在哪里
$V_s$ = 饱和载流子漂移速度
$L$ = 样本长度
这里计算的通过时间是注射和收集之间的时间。重复的动作增加了输出,使其成为放大器,而与电路并联的微波低通滤波器可以使其作为振荡器工作。
应用领域
这种二极管有很多应用。
- 低功率多普勒雷达
- 雷达本地振荡器
- 微波信标着陆系统
- 无线电高度计
- 相控阵雷达等
巴里特二极管
BARITT 二极管的完整形式是 BARrier 注入传输时间二极管。这些是该家族的最新发明。尽管这些二极管与 IMPATT 二极管一样具有长漂移区,但 BARITT 二极管中的载流子注入是由正向偏置结引起的,而不是像它们那样来自雪崩区域的等离子体。
在 IMPATT 二极管中,由于碰撞电离,载流子注入的噪声非常大。在 BARITT 二极管中,为了避免噪声,通过耗尽区的穿通来提供载流子注入。BARITT 二极管中的负电阻是由于注入的空穴漂移到由 p 型材料制成的二极管的集电极端而获得的。
下图显示了 BARITT 二极管的结构细节。

对于mnm BARITT 二极管,Ps-Si肖特基势垒与金属接触,n 型硅晶圆位于其间。由于热电子空穴注入半导体,电流随着施加电压(高于 30v)而快速增加。
临界电压 $(Vc)$ 取决于掺杂常数 $(N)$、半导体长度 $(L)$ 和半导体介电常数 $(\epsilon S)$,表示为
$$V_c = \frac{qNL^2}{2\epsilon S}$$
单片微波集成电路 (MMIC)
微波 IC 是传统波导或同轴电路的最佳替代品,因为它们重量轻、尺寸小、高度可靠且可重复。用于单片微波集成电路的基本材料是 -
- 基材材质
- 导体材质
- 介电薄膜
- 电阻膜
这些被选择为具有理想的特性和高效率。制造电路元件的基板非常重要,因为材料的介电常数应该较高,损耗因数较低,并且具有其他理想特性。使用的基板材料有砷化镓、铁氧体/石榴石、铝、铍、玻璃和金红石。
导体材料的选择应具有高导电率、低电阻温度系数、与基材的附着力好、蚀刻性好等特点。导体材料主要采用铝、铜、金、银等。所选择的介电材料和电阻材料具有低损耗和良好的稳定性。
制造技术
在混合集成电路中,半导体器件和无源电路元件形成在介电基板上。无源电路要么是分布式元件,要么是集总元件,或者是两者的组合。
混合集成电路有两种类型。
- 混合集成电路
- 微型混合IC
在上述两种工艺中,混合 IC 使用采用单层金属化技术在 IC 上制造的分布式电路元件,而微型混合 IC 使用多层元件。
大多数模拟电路使用介观隔离技术来隔离用于 FET 和二极管的有源 n 型区域。平面电路是通过将离子注入半绝缘衬底来制造的,并且为了提供隔离,该区域被遮蔽。
在GaAs FET中,采用“过孔”技术将源极与源极接地,如下图所示。

MMIC 有很多应用。
- 军事通讯
- 雷达
- 细胞外基质
- 相控阵天线系统
- 扩频和 TDMA 系统
它们具有成本效益,也用于许多国内消费应用,如 DTH、电信和仪器仪表等。
微波工程 - 微波器件
与其他系统一样,微波系统由许多微波组件组成,主要是一端为源,另一端为负载,这些组件均通过波导或同轴电缆或传输线系统连接。
以下是波导的特性。
- 高信噪比
- 低衰减
- 更低的插入损耗
波导微波功能
考虑有 4 个端口的波导。如果将电源施加到一个端口,则电源会按一定比例流经所有 3 个端口,其中一些电源可能会从同一端口反射回来。下图清楚地描述了这个概念。

散射参数
对于双端口网络,如下图所示,如果在一个端口上供电,正如我们刚才讨论的那样,大部分功率会从另一个端口逸出,而其中一些会反射回同一端口。在下图中,如果施加V 1或V 2 ,则分别流过I 1或I 2电流。

如果源应用到相反的端口,则要考虑另外两种组合。因此,对于双端口网络,可能会出现 2 × 2 = 4 种组合。
具有相关功率的行波通过端口散射出去时,微波结可以通过 S 参数或散射参数来定义,它们以矩阵形式表示,称为“散射矩阵”。
散射矩阵
它是一个方阵,给出了微波结的各个输入和输出端口之间的功率关系的所有组合。该矩阵的元素称为“散射系数”或“散射(S)参数”。
考虑下图。

这里,源通过$i^{th}$线连接,而$a_1$是入射波,$b_1$是反射波。
如果 $b_1$ 和 $a_1$ 之间存在关系,
$$b_1 = (反射 \: \: 系数)a_1 = S_{1i}a_1$$
在哪里
$S_{1i}$ = $1^{st}$ 线的反射系数(其中 $i$ 是输入端口,$1$ 是输出端口)
$1$ = $1^{st}$ 线的反射
$i$ = 在 $i^{th}$ 行连接的源
如果阻抗匹配,则功率就会传输到负载。如果负载阻抗与特性阻抗不匹配,则不太可能。然后,就会发生反射。这意味着,如果发生反射
$$Z_l \neq Z_o$$
但是,如果多个端口存在这种不匹配,例如 $'n'$ 端口,则 $i = 1$ 到 $n$(因为 $i$ 可以是从 $1$ 到 $n$ 的任何行)。
因此,我们有
$$b_1 = S_{11}a_1 + S_{12}a_2 + S_{13}a_3 + ........................ + S_{1n}a_n$$
$$b_2 = S_{21}a_1 + S_{22}a_2 + S_{23}a_3 + ........................ + S_{2n}a_n$$
$$.$$
$$.$$
$$.$$
$$.$$
$$.$$
$$b_n = S_{n1}a_1 + S_{n2}a_2 + S_{n3}a_3 + ........................ + S_{nn}a_n$$
当这整个事情以矩阵形式保存时,
$$\begin{bmatrix} b_1\\ b_2\\ b_3\\ .\\ .\\ .\\ b_n \end{bmatrix} = \begin{bmatrix} S_{11}& S_{12}& S_{13 }& ...& S_{1n}\\ S_{21}& S_{22}& S_{23}& ...& S_{2n}\\ .& .& .& ...& . \\ .& .& .& ...& . \\ .& .& .& ...& . \\ S_{n1}& S_{n2}& S_{n3}& ...& S_{nn}\\ \end{bmatrix} \times \begin{bmatrix} a_1\\ a_2\\ a_3\\ .\ \ .\\ .\\ a_n \end{bmatrix}$$
列矩阵$[b]$散射矩阵$[S]$矩阵$[a]$
列矩阵 $\left [ b \right ]$ 对应于反射波或输出,而矩阵 $\left [ a \right ]$ 对应于入射波或输入。散射列矩阵 $\left [ s \right ]$ 的量级为 $n \times n$,包含反射系数和透射系数。所以,
$$\left [ b \right ] = \left [ S \right ]\left [ a \right ]$$
[S] 矩阵的性质
散射矩阵表示为 $[S]$ 矩阵。$[S]$ 矩阵的标准属性很少。他们是 -
-
$[S]$ 始终是阶数为 (nxn) 的方阵
$[S]_{n \乘n}$
-
$[S]$ 是对称矩阵
即$S_{ij} = S_{ji}$
-
$[S]$ 是酉矩阵
即 $[S][S]^* = I$
任何行或列的每一项乘以任何其他行或列的相应项的复共轭的乘积之和为零。IE,
$$\sum_{i=j}^{n} S_{ik} S_{ik}^{*} = 0 \: 对于 \: k \neq j$$
$$( k = 1,2,3, ... \: n ) \: 和 \: (j = 1,2,3, ... \: n)$$
-
如果某个 $k^{th}$ 端口与结点之间的电气距离为 $\beta _kI_k$,则涉及 $k$ 的 $S_{ij}$ 系数将乘以系数 $e^{- j\beta kIk}$
在接下来的几章中,我们将了解不同类型的微波 T 形接头。
微波工程 - E-Plane T 恤
E-Plane T 形接头是通过将简单波导连接到矩形波导的更宽尺寸上而形成的,该矩形波导已经具有两个端口。矩形波导的臂形成两个端口,称为共线端口,即端口 1 和端口 2,而新的端口 端口 3 称为侧臂或E 臂。该 E-plane T 恤也称为系列 T 恤。
由于侧臂的轴线平行于电场,因此该结点被称为E-Plane Tee结点。这也称为电压或串联结。端口 1 和 2 彼此相差 180°。E平面三通的截面细节可以通过下图来了解。

下图显示了侧臂与双向波导形成并行端口的连接。

E-Plane T 恤的特性
E-Plane Tee 的属性可以通过其 $[S]_{3x3}$ 矩阵来定义。
它是一个 3×3 矩阵,因为有 3 个可能的输入和 3 个可能的输出。
$[S] = \begin{bmatrix} S_{11}& S_{12}& S_{13}\\ S_{21}& S_{22}& S_{23}\\ S_{31}& S_{32 }& S_{33} \end{bmatrix}$ ........ 等式 1
散射系数 $S_{13}$ 和 $S_{23}$ 与端口 3 处的输入异相 180°。
$S_{23} = -S_{13}$ ........ 等式 2
该港口与路口完美匹配。
$S_{33} = 0$ ........ 等式 3
由对称性可知,
$S_{ij} = S_{ji}$
$S_{12} = S_{21} \: \: S_{23} = S_{32} \: \: S_{13} = S_{31}$ ........ 公式 4
考虑方程 3 和 4,$[S]$ 矩阵可以写为,
$[S] = \begin{bmatrix} S_{11}& S_{12}& S_{13}\\ S_{12}& S_{22}& -S_{13}\\ S_{13}& -S_ {13}& 0 \end{bmatrix}$ ........ 等式 5
考虑到对称性,我们可以说我们有四个未知数。
从单一财产
$$[S][S]\ast = [I]$$
$$\begin{bmatrix} S_{11}& S_{12}& S_{13}\\ S_{12}& S_{22}& -S_{13}\\ S_{13}& -S_{13} & 0 \end{bmatrix} \: \begin{bmatrix} S_{11}^{*}& S_{12}^{*}& S_{13}^{*}\\ S_{12}^{*} & S_{22}^{*}& -S_{13}^{*}\\ S_{13}^{*}& -S_{13}^{*}& 0 \end{bmatrix} = \begin{ bmatrix} 1& 0& 0\\ 0& 1& 0\\ 0& 0& 1 \end{bmatrix}$$
相乘我们得到,
(注意 R 为行,C 为列)
$R_1C_1 : S_{11}S_{11}^{*} + S_{12}S_{12}^{*} + S_{13}S_{13}^{*} = 1$
$\左 | S_{11} \right |^2 + \left | S_{11} \right |^2 + \left | S_{11} \right |^2 = 1$ ........ 等式 6
$R_2C_2 : \left | S_{12} \right |^2 + \left | S_{22} \right |^2 + \left | S_{13} \right |^2 = 1$ …… 等式 7
$R_3C_3 : \left | S_{13} \right |^2 + \left | S_{13} \right |^2 = 1$ …… 等式 8
$R_3C_1 : S_{13}S_{11}^{*} - S_{13}S_{12}^{*} = 1$ ......... 公式 9
等式 6 和 7 相等,我们得到
$S_{11} = S_{22} $ ........ 公式 10
根据公式 8,
$2\左| S_{13} \right |^2 \quad 或 \quad S_{13} = \frac{1}{\sqrt{2}}$ ......... 方程 11
根据公式 9,
$S_{13}\左 ( S_{11}^{*} - S_{12}^{*} \右 )$
或 $S_{11} = S_{12} = S_{22}$ ...... 公式 12
使用等式 6 中的等式 10、11 和 12,
我们得到,
$\左| S_{11} \right |^2 + \left | S_{11} \right |^2 + \frac{1}{2} = 1$
$2\左| S_{11} \right |^2 = \frac{1}{2}$
或 $S_{11} = \frac{1}{2}$ ...... 方程 13
将上述方程中的值代入 $[S]$ 矩阵,
我们得到,
$$\left [ S \right ] = \begin{bmatrix} \frac{1}{2}& \frac{1}{2}& \frac{1}{\sqrt{2}}\\ \frac{ 1}{2}& \frac{1}{2}& -\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}& -\frac{1}{ \sqrt{2}}& 0 \end{bmatrix}$$
我们知道 $[b]$ = $[S] [a]$
$$\begin{bmatrix}b_1 \\ b_2 \\ b_3 \end{bmatrix} = \begin{bmatrix} \frac{1}{2}& \frac{1}{2}& \frac{1}{1}{\ sqrt{2}}\\ \frac{1}{2}& \frac{1}{2}& -\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2 }}& -\frac{1}{\sqrt{2}}& 0 \end{bmatrix} \begin{bmatrix} a_1\\ a_2\\ a_3 \end{bmatrix}$$
这是 E-Plane Tee 的散射矩阵,解释了其散射特性。
微波工程 - H 平面三通
H 平面 T 形接头是通过将简单波导连接到已具有两个端口的矩形波导而形成的。矩形波导的臂形成两个端口,称为共线端口,即端口 1 和端口 2,而新端口端口 3 称为侧臂或H 臂。这种 H 平面三通也称为分流三通。
由于侧臂的轴线与磁场平行,因此该结点称为 H 平面 T 形结。这也称为电流结,因为磁场将自身分成臂。H型三通的截面细节可以通过下图来了解。

下图显示了侧臂与双向波导形成串口的连接。

H 平面三通的特性
H-Plane Tee 的属性可以通过其 $\left [ S \right ]_{3\times 3}$ 矩阵来定义。
它是一个 3×3 矩阵,因为有 3 个可能的输入和 3 个可能的输出。
$[S] = \begin{bmatrix} S_{11}& S_{12}& S_{13}\\ S_{21}& S_{22}& S_{23}\\ S_{31}& S_{32 }& S_{33} \end{bmatrix}$ ........ 等式 1
由于连接点在平面上对称,因此散射系数 $S_{13}$ 和 $S_{23}$ 相等。
由对称性可知,
$S_{ij} = S_{ji}$
$S_{12} = S_{21} \: \: S_{23} = S_{32} = S_{13} \: \: S_{13} = S_{31}$
端口完美匹配
$S_{33} = 0$
现在,$[S]$ 矩阵可以写成:
$[S] = \begin{bmatrix} S_{11}& S_{12}& S_{13}\\ S_{12}& S_{22}& S_{13}\\ S_{13}& S_{13 }& 0 \end{bmatrix}$ ........ 等式 2
考虑到对称性,我们可以说我们有四个未知数。
从单一财产
$$[S][S]\ast = [I]$$
$$\begin{bmatrix} S_{11}& S_{12}& S_{13}\\ S_{12}& S_{22}& S_{13}\\ S_{13}& S_{13}& 0 \end{bmatrix} \: \begin{bmatrix} S_{11}^{*}& S_{12}^{*}& S_{13}^{*}\\ S_{12}^{*}& S_ {22}^{*}& S_{13}^{*}\\ S_{13}^{*}& S_{13}^{*}& 0 \end{bmatrix} = \begin{bmatrix} 1& 0& 0\\ 0& 1& 0 \\ 0& 0& 1 \end{bmatrix}$$
相乘我们得到,
(注意 R 为行,C 为列)
$R_1C_1 : S_{11}S_{11}^{*} + S_{12}S_{12}^{*} + S_{13}S_{13}^{*} = 1$
$\左 | S_{11} \right |^2 + \left | S_{12} \right |^2 + \left | S_{13} \right |^2 = 1$ ........ 等式 3
$R_2C_2 : \left | S_{12} \right |^2 + \left | S_{22} \right |^2 + \left | S_{13} \right |^2 = 1$ ......... 方程 4
$R_3C_3 : \left | S_{13} \right |^2 + \left | S_{13} \right |^2 = 1$ …… 等式 5
$R_3C_1 : S_{13}S_{11}^{*} - S_{13}S_{12}^{*} = 0$ ......... 公式 6
$2\左| S_{13} \right |^2 = 1 \quad 或 \quad S_{13} = \frac{1}{\sqrt{2}}$ ......... 方程 7
