VLSI 设计 - MOS 晶体管

互补 MOSFET (CMOS) 技术如今被广泛用于在众多不同的应用中形成电路。当今的计算机、CPU 和手机都使用 CMOS，因为它有几个关键优势。CMOS 在两种状态下都具有低功耗、相对较高的速度和高噪声容限，并且可在较宽的源电压和输入电压范围内运行（假设源电压固定）

对于我们将讨论的工艺，可用的晶体管类型是金属氧化物半导体场效应晶体管 (MOSFET)。这些晶体管形成为“三明治”，由半导体层组成，通常是硅单晶的切片或晶片；一层二氧化硅（氧化物）和一层金属。

MOSFET的结构

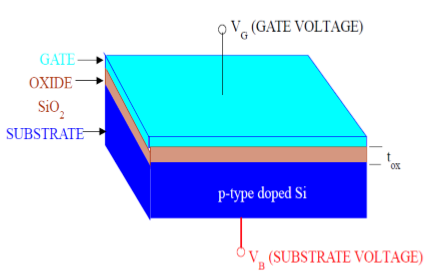
如图所示，MOS结构包含三层 -

金属栅电极
绝缘氧化层 (SiO ₂ )
P型半导体（基板）

MOS结构形成一个电容器，栅极和衬底作为两块极板，氧化层作为介电材料。_{介电材料(SiO 2} )的厚度通常在10nm至50nm之间。衬底内的载流子浓度和分布可以通过施加到栅极和衬底端子的外部电压来控制。现在，要了解MOS的结构，首先要考虑P型半导体衬底的基本电特性。

半导体材料中载流子的浓度始终遵循质量作用定律。群体行动法由下式给出 -

$$np=n_{i}^{2}$$

在哪里，

n是电子的载流子浓度
p是空穴的载流子浓度
n _i是硅的本征载流子浓度

现在假设衬底同样掺杂有浓度 N _A的受主（硼）。因此，p型衬底中的电子和空穴浓度为

$$n_{po}=\frac{n_{i}^{2}}{N_{A}}$$

$$p_{po}=N_{A}$$

这里，掺杂浓度N _A比本征浓度ni大(10 ¹⁵～10 ¹⁶ cm ^-3 )。现在，为了理解 MOS 结构，请考虑 p 型硅衬底的能级图。

如图所示，导带和价带之间的带隙为1.1eV。这里，费米势 Φ _{F是本征费米能级 (E}_i ) 和费米能级 (E _FP )之间的差值。

其中费米能级 E _F取决于掺杂浓度。费米势 Φ _{F是本征费米能级 (E}_i ) 和费米能级 (E _FP )之间的差值。

从数学上来说，

$$\Phi_{Fp}=\frac{E_{F}-E_{i}}{q}$$

导带和自由空间之间的电势差称为电子亲和势，用 qx 表示。

因此，电子从费米能级移动到自由空间所需的能量称为功函数 (qΦ _S )，由下式给出

$$q\Phi _{s}=(E_{c}-E_{F})+qx$$

下图是组成MOS的元件的能带图。

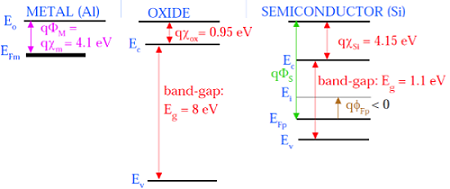
如上图所示，绝缘SiO ₂层具有8eV的大能带隙，功函数为0.95 eV。金属栅极的功函数为4.1eV。这里，功函数不同，因此会在 MOS 系统上产生压降。下图为MOS系统的组合能带图。

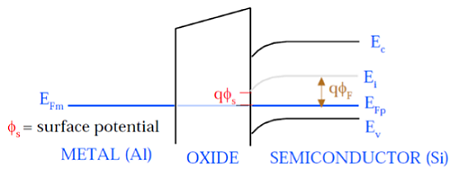
如图所示，金属栅极和半导体（Si）的费米电势水平处于相同电势。表面的费米势称为表面势 Φ _S，其大小小于费米势 Φ _{F 。}

MOSFET 的工作原理

MOSFET 由一个 MOS 电容器和两个靠近沟道区域的 pn 结组成，该区域由栅极电压控制。为了使pn结反向偏置，衬底电位保持低于其他三个端子电位。

如果栅极电压升高到超过阈值电压（V _GS >V _TO），表面就会形成反型层，源极和漏极之间就会形成n型沟道。该n型通道将根据V _DS值承载漏极电流。

_{对于不同的 V DS}值，MOSFET 可以工作在不同的区域，如下所述。

线性区域

当 V _DS = 0 时，反向沟道区存在热平衡，漏极电流 I _D = 0。现在，如果施加小漏极电压，V _{DS > 0，则与 V}_DS成比例的漏极电流将开始从源极流向通过通道排出。

该沟道为电流从源极到漏极的流动提供了连续的路径。这种操作模式称为线性区域。工作在线性区的 n 沟道 MOSFET 的横截面图如下图所示。

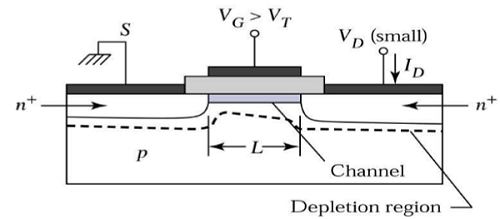
处于饱和区边缘

现在，如果 V _DS增加，沟道中的电荷和沟道深度在漏极末端会减少。当V _DS = V _DSAT时，沟道中的电荷减少至零，这称为夹断点。工作在饱和区边缘的n沟道MOSFET的横截面图如下图所示。

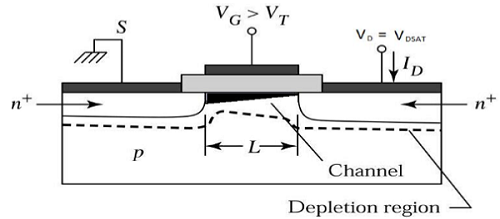
饱和区

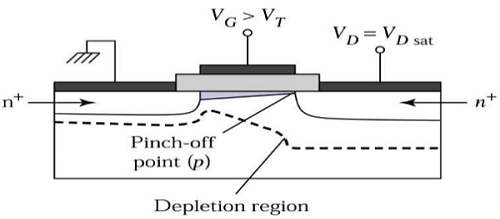
当V _DS >V _DSAT时，在漏极附近形成耗尽表面，并且通过增加漏极电压，该耗尽区域延伸至源极。

这种工作模式称为饱和区。电子从源极到达沟道端，进入漏极耗尽区，并在高电场中向漏极加速。

MOSFET 电流-电压特性

为了了解 MOSFET 的电流-电压特性，需要对通道进行近似。如果没有这种近似，MOS 系统的三维分析就会变得复杂。电流-电压特性的渐进通道近似（GCA）将减少分析问题。

渐进通道逼近 (GCA)

考虑在线性模式下工作的 n 沟道 MOSFET 的横截面图。这里，源极和基板接地。V _S = V _B = 0。栅极至源极电压 (V _GS ) 和漏极至源极电压 (V _DS ) 电压是控制漏极电流 I _D的外部参数。

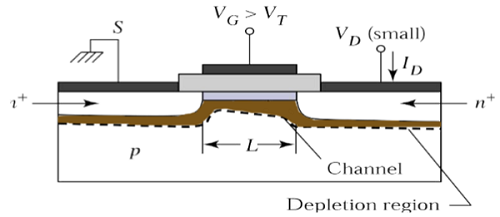
将电压V _GS设置为大于阈值电压V _TO的电压，以在源极和漏极之间创建沟道。如图所示，x方向垂直于表面，y方向平行于表面。

这里，如图所示，源端 y = 0。相对于源极的沟道电压由V _C(Y)表示。假设阈值电压 VTO 在 y = 0 到 y = L 之间沿沟道区域恒定。沟道电压 V _C的边界条件为 -

$$V_{c}\left ( y = 0 \right ) = V_{s} = 0 \,and\,V_{c}\left ( y = L \right ) = V_{DS}$$

我们还可以假设

$$V_{GS}\geq V_{TO}$$和

$$V_{GD} = V_{GS}-V_{DS}\geq V_{TO}$$

令 Q1(y) 为表面反型层中的总移动电子电荷。该电子电荷可以表示为 -

$$Q1(y)=-C_{ox}.[V_{GS}-V_{C(Y)}-V_{TO}]$$

下图显示了地表逆温层的空间几何形状并指出了其尺寸。当我们从漏极移动到源极时，反演层逐渐减小。现在，如果我们考虑沟道长度 L 的小区域 dy，则该区域提供的增量电阻 dR 可以表示为 -

$$dR=-\frac{dy}{w.\mu _{n}.Q1(y)}$$

这里，负号是由于反型层电荷Q1的负极性而引起的，μ _n是表面迁移率，其是恒定的。现在，将 Q1(y) 的值代入 dR 方程 -

$$dR=-\frac{dy}{w.\mu _{n}.\left \{ -C_{ox}\left [ V_{GS}-V_{C\left ( Y \right )} \right ]-V_{TO} \右\}}$$

$$dR=\frac{dy}{w.\mu _{n}.C_{ox}\left [ V_{GS}-V_{C\left ( Y \right )} \right ]-V_{TO} }$$

现在小 dy 区域的电压降可以由下式给出

$$dV_{c}=I_{D}.dR$$

将dR的值代入上式

$$dV_{C}=I_{D}.\frac{dy}{w.\mu_{n}.C_{ox}\left [ V_{GS}-V_{C(Y)} \right ]-V_ {致}}$$

$$w.\mu _{n}.C_{ox}\left [ V_{GS}-V_{C(Y)}-V_{TO} \right ].dV_{C}=I_{D}.dy $$

为了获得整个沟道区域的漏极电流 ID，可以沿沟道从 y = 0 到 y = L 以及电压 V _C(y) = 0 到 V _C(y) = V _DS对上述方程进行积分，

$$C_{ox}.w.\mu _{n}.\int_{V_{c}=0}^{V_{DS}} \left [ V_{GS}-V_{C\left ( Y \right )}-V_{TO} \right ].dV_{C} = \int_{Y=0}^{L}I_{D}.dy$$

$$\frac{C_{ox}.w.\mu _{n}}{2}\left ( 2\left [ V_{GS}-V_{TO} \right ] V_{DS}-V_{DS} ^{2}\right ) = I_{D}\left [ L-0 \right ]$$

$$I_{D} = \frac{C_{ox}.\mu _{n}}{2}.\frac{w}{L}\left ( 2\left [ V_{GS}-V_{TO} \right ]V_{DS}-V_{DS}^{2} \right )$$

对于线性区域 V _DS < V _GS – V _TO。对于饱和区，V _DS的值大于(V _GS -V _TO )。因此，对于饱和区，V _DS = (V _GS – V _TO )。

$$I_{D} = C_{ox}.\mu _{n}.\frac{w}{2}\left ( \frac{\left [ 2V_{DS} \right ]V_{DS}-V_{ DS}^{2}}{L} \右)$$

$$I_{D} = C_{ox}.\mu _{n}.\frac{w}{2}\left ( \frac{2V_{DS}^{2}-V_{DS}^{2} {L} \右）$$

$$I_{D} = C_{ox}.\mu _{n}.\frac{w}{2}\left ( \frac{V_{DS}^{2}}{L} \right )$$

$$I_{D} = C_{ox}.\mu _{n}.\frac{w}{2}\left ( \frac{\left [ V_{GS}-V_{TO} \right ]^{ 2}}{L} \右）$$