
- 基础电子教程
- 基础电子 - 主页
基础电子产品 - 快速指南
基础电子 - 材料
物质由分子组成,分子又由Atomics组成。根据玻尔的理论,“Atomics由带正电的Atomics核和许多带负电的电子组成,这些电子围绕Atomics核以各种轨道旋转”。当电子从较低态提升到较高态时,称为被激发。在激发时,如果电子完全从Atomics核中移出,则Atomics被电离。因此,Atomics从正常状态提升到电离状态的过程称为电离。
下图显示了Atomics的结构。

根据玻尔模型,电子被认为在特定的轨道中移动,而根据量子力学,电子被认为位于Atomics自由空间中的某个位置,称为轨道。这个量子力学理论被证明是正确的。因此,可能发现电子的三维边界称为Atomics轨道。
量子数
电子移动的每个轨道的能量和形状都不同。轨道的能级可以使用称为量子数的离散积分和半积分集来表示。有四个量子数用于定义波函数。
主量子数
描述电子的第一个量子数是主量子数。它的符号是n。它指定数字的大小或顺序(能级)。随着n值的增加,电子到Atomics核的平均距离也增加,电子的能量也增加。主能级可以理解为外壳。
角动量量子数
这个量子数以l为符号。这个l表示轨道的形状。其范围从0到n-1。
l = 0, 1, 2 …n-1
对于第一个壳,n = 1。
即,对于 n-1,l = 0 是 n = 1 时 l 的唯一可能值。
因此,当l = 0时,称为S轨道。S的形状是球形的。下图表示S的形状。

如果 n = 2,则 l = 0、1,因为这是 n = 2 的两个可能值。
我们知道当l = 0时它是S轨道,但如果l = 1,它是P轨道。
电子更容易找到的 P 轨道呈哑铃形。如下图所示。

磁量子数
该量子数用m l表示,表示围绕Atomics核的轨道的方向。m l的值取决于 l。
$$m_{l}= \int (-l\:\:到\:+l)$$
当 l = 0、m l = 0 时,这代表 S 轨道。
对于 l = 1、m l = -1、0、+1,这是三个可能的值,这代表 P 轨道。
因此我们有三个 P 轨道,如下图所示。

自旋量子数
这用m s表示,这里的电子在轴上旋转。电子旋转的运动可以是顺时针或逆时针,如下所示。

该自旋量子数的可能值如下:
$$m_{s}= +\frac{1}{2}\:\:上$$
对于称为旋转向上的运动,结果是正一半。
$$m_{s}= -\frac{1}{2}\:\:向下$$
对于称为旋转下降的运动,结果是负一半。
这是四个量子数。
泡利不相容原理
根据泡利不相容原理,Atomics中没有两个电子可以具有相同的四个相同量子数。这意味着,如果任何两个电子具有相同的 n、s、ml 值(正如我们上面刚刚讨论的),那么它们的 l 值肯定会不同。因此,没有两个电子具有相同的能量。
电子外壳
如果 n = 1 是壳层,则 l = 0 是子壳层。
同样,n = 2 是一个壳层,l = 0, 1 是一个子壳层。
n=1、2、3……对应的电子壳层分别用K、L、M、N表示。对应于l = 0、1、2、3等的子壳层或轨道分别用s、p、d、f等表示。

让我们看一下碳、硅和锗(IV-A 族)的电子排布。

据观察,每种情况下最外层的 p 子壳层仅包含两个电子。但电子的可能数量是六个。因此,每个最外层都有四个价电子。因此,Atomics中的每个电子都具有特定的能量。任何物质的分子内部的Atomics排列几乎都是这样的。但Atomics之间的间距因材料而异。
基础电子学 - 能带
在气态物质中,分子的排列并不紧密。在液体中,分子排列是中等的。但是,在固体中,分子排列非常紧密,分子Atomics中的电子往往会移动到相邻Atomics的轨道中。因此,当Atomics聚集在一起时,电子轨道重叠。
由于固体中Atomics的混合,不会形成单一能级,而是形成能级带。这些紧密排列的能级集合称为能带。
价带
电子在Atomics中以一定的能级运动,但最内层电子的能量高于最外层电子。最外层电子的电子称为价电子。
这些包含一系列能级的价电子形成一个能带,称为价带。价带是具有最高占据能量的能带。
导带
价电子与Atomics核的结合非常松散,即使在室温下,也很少有价电子离开能带是自由的。这些电子被称为自由电子,因为它们倾向于向邻近的Atomics移动。
这些自由电子在导体中传导电流,因此称为传导电子。含有传导电子的能带称为导带。导带是具有最低占据能量的带。
禁止间隙
价带和导带之间的间隙称为禁带能隙。顾名思义,这一带是没有能量的禁带。因此没有电子留在该带中。价电子在进入导带时会穿过导带。
禁带间隙越大,意味着价带电子与Atomics核紧密结合。现在,为了将电子推出价带,需要一些外部能量,该能量等于禁带能隙。
下图显示了价带、导带和禁带。

根据禁带间隙的大小,形成绝缘体、半导体和导体。
绝缘子
绝缘体是由于禁隙较大而无法导电的材料。例如:木材、橡胶。绝缘体中的能带结构如下图所示。

特征
以下是绝缘子的特性。
禁断能量差距非常大。
价带电子与Atomics紧密结合。
绝缘体的禁带能隙值为 10eV。
对于某些绝缘体,随着温度升高,它们可能会表现出一定的导电性。
绝缘体的电阻率约为 107 欧姆米。
半导体
半导体是禁带能隙很小的材料,如果施加一些外部能量就会发生传导。例如:硅、锗。下图显示了半导体中的能带结构。
特征
以下是半导体的特性。
禁断能隙很小。
Ge 的禁带宽度为 0.7eV,而 Si 的禁带宽度为 1.1eV。
半导体实际上既不是绝缘体,也不是良导体。
随着温度升高,半导体的电导率增加。
半导体的电导率约为 102 毫欧米。
导体
导体是这样的材料,其中当价带和导带变得非常接近且重叠时,禁带间隙消失。例如:铜、铝。下图显示了导体中的能带结构。

特征
以下是导体的特性。
导体中不存在禁止间隙。
价带和导带重叠。
可用于传导的自由电子是充足的。
电压稍微增加,传导就会增加。
不存在空穴形成的概念,因为连续的电子流贡献电流。
重要条款
在我们继续后续章节之前,有必要在这里讨论一些重要的术语。
当前的
这只是电子的流动。电子或带电粒子的连续流动可以称为电流。用I或i表示。它以安培为单位测量。这可以是交流电AC或直流电DC。
电压
这就是潜在的差异。当两点之间出现电位差时,就称在这两点之间测量到了电压差。用V表示。它以伏特为单位。
反抗
它是对抗电子流动的特性。拥有这种特性可以称为电阻率。这将在后面详细讨论。
欧姆定律
通过上面讨论的术语,我们有了一个标准定律,它对于所有电子元件的Behave都非常重要,称为欧姆定律。这说明了理想导体中电流和电压之间的关系。
根据欧姆定律,理想导体上的电势差与通过它的电流成正比。
$$V\:\alpha\:\:I$$
理想导体没有电阻。但实际上,每个导体都有一定的电阻。随着电阻增加,电势降也增加,因此电压增加。
因此,电压与其提供的电阻成正比。
$$V\:\alpha\:\:R$$
$$V = IR $$
但电流与电阻成反比。
$$V\:\alpha\:\:I\:\alpha\:\:\frac{1}{R}$$
$$I = V/R $$
因此,在实践中,欧姆定律可以表述为 -
根据欧姆定律,流过导体的电流与导体两端的电位差成正比,与导体提供的电阻成反比。
该定律有助于确定三个参数中未知参数的值,从而有助于分析电路。
基础电子 - 半导体
半导体是电阻率介于导体和绝缘体之间的物质。电阻率的性质并不是决定材料是否为半导体的唯一性质,但它具有以下几个性质。
半导体的电阻率小于绝缘体而大于导体。
半导体具有负温度系数。半导体的电阻随着温度的降低而增加,反之亦然。
当添加合适的金属杂质时,半导体的导电特性会发生变化,这是一个非常重要的特性。
半导体器件广泛应用于电子领域。晶体管取代了笨重的真空管,从而减小了设备的尺寸和成本,并且这场革命不断加快步伐,带来了集成电子产品等新发明。下图显示了半导体的分类。
半导体中的传导
在对电子有了一些了解之后,我们知道最外层的电子是价电子,它们松散地附着在Atomics核上。这样的Atomics具有价电子,当靠近另一个Atomics时,这两个Atomics的价电子结合形成“电子对”。这种键合不是很强,因此它是共价键。
例如,锗Atomics有 32 个电子。第一个轨道有 2 个电子,第二个轨道有 8 个电子,第三个轨道有 18 个电子,最后一个轨道有 4 个电子。这4个电子是锗Atomics的价电子。这些电子倾向于与相邻Atomics的价电子结合,形成电子对,如下图所示。

孔的创建
由于向晶体提供热能,一些电子往往会移出其位置并破坏共价键。这些断裂的共价键产生随机漂移的自由电子。但是移走的电子在后面产生了一个空的空间或价态,称为空穴。
代表缺失电子的空穴可以被视为单位正电荷,而电子被视为单位负电荷。释放的电子随机移动,但当施加一些外部电场时,这些电子沿与施加的场相反的方向移动。但由于缺乏电子而产生的空穴会沿施加场的方向移动。
空穴电流
人们已经知道,当共价键断裂时,就会产生一个孔。实际上,半导体晶体有很强的形成共价键的倾向。因此,晶体中往往不存在空穴。通过下图可以更好地理解这一点,该图显示了半导体晶格。

当电子从位置A移动时,形成空穴。由于形成共价键的趋势,电子从 B 转移到 A。现在,再次为了平衡 B 处的共价键,电子从 C 转移到 B。这继续构建一条路径。在没有施加场的情况下,孔的这种运动是随机的。但当施加电场时,空穴沿着施加的场漂移,这就构成了空穴电流。这被称为空穴电流而不是电子电流,因为空穴的移动贡献了电流。
电子和空穴在随机运动时可能会彼此相遇,形成对。这种重组导致热量释放,从而破坏另一个共价键。当温度升高时,电子和空穴的产生速率增加,复合速率增加,导致电子和空穴的密度增加。结果,半导体的电导率增加,电阻率降低,这意味着负温度系数。
本征半导体
极其纯净的半导体被称为本征半导体。这种纯半导体的特性如下 -
- 电子和空穴仅由热激发产生。
- 自由电子的数量等于空穴的数量。
- 室温下导电能力较小。
为了增加本征半导体的导电能力,最好添加一些杂质。这种添加杂质的过程称为掺杂。现在,这种掺杂的本征半导体被称为非本征半导体。
兴奋剂
向半导体材料添加杂质的过程称为掺杂。添加的杂质通常是五价和三价杂质。
五价杂质
五价杂质是在最外层轨道上具有五个价电子的杂质。例如:铋、锑、砷、磷
五价Atomics被称为施主Atomics,因为它向纯半导体Atomics的导带提供一个电子。
三价杂质
三价杂质是在最外层轨道具有三个价电子的杂质。示例:镓、铟、铝、硼
三价Atomics被称为受体Atomics,因为它接受来自半导体Atomics的一个电子。
外来半导体
通过掺杂纯半导体而形成的不纯半导体称为非本征半导体。根据添加的杂质类型,有两种类型的非本征半导体。它们是N型非本征半导体和P型非本征半导体。
N型非本征半导体
在纯半导体中添加少量五价杂质,形成N型非本征半导体。添加的杂质具有5个价电子。
例如,如果将砷Atomics添加到锗Atomics中,则四个价电子与GeAtomics结合,而一个电子保留为自由电子。如下图所示。
所有这些自由电子构成电子流。因此,当添加到纯半导体中时,杂质会提供用于传导的电子。
在N型非本征半导体中,由于传导是通过电子进行的,因此电子是多数载流子,空穴是少数载流子。
由于没有添加正电荷或负电荷,因此电子呈电中性。
当向添加有五价杂质的N型半导体施加电场时,自由电子向正极移动。这称为负电导率或 N 型电导率。
P型非本征半导体
在纯半导体中添加少量三价杂质,形成P型非本征半导体。添加的杂质具有3个价电子。例如,如果将硼Atomics添加到锗Atomics中,则三个价电子与GeAtomics结合,形成三个共价键。但是,锗中还有一个电子未形成任何键。由于硼中没有留下形成共价键的电子,因此该空间被视为空穴。如下图所示。
当添加少量硼杂质时,会提供许多有助于导电的孔。所有这些空穴构成空穴电流。
在P型非本征半导体中,由于传导是通过空穴进行的,因此空穴是多数载流子,而电子是少数载流子。
这里添加的杂质提供了被称为受主的空穴,因为它们接受来自锗Atomics的电子。
由于移动空穴的数量保持等于受主的数量,因此 P 型半导体保持电中性。
当向添加了三价杂质的 P 型半导体施加电场时,空穴向负极移动,但速度比电子慢。这称为P型导电性。
在这种 P 型导电性中,价电子从一个共价键移动到另一个共价键,这与 N 型不同。
为什么半导体首选硅?
在锗、硅等半导体材料中,广泛用于制造各种电子元件的材料是硅(Si)。由于多种原因,硅优于锗,例如 -
能带隙为 0.7ev,而锗为 0.2ev。
热对产生较小。
SiO2 层对于硅来说很容易形成,这有助于许多组件的制造以及集成技术。
Si 在自然界中比 Ge 更容易找到。
由 Si 制成的元件的噪声比由 Ge 制成的元件低。
因此,硅用于制造许多电子元件,这些电子元件用于制造用于各种目的的不同电路。这些组件具有各自的属性和特定的用途。
主要电子元件包括——电阻器、可变电阻器、电容器、可变电容器、电感器、二极管、隧道二极管、变容二极管、晶体管、BJT、UJT、FET、MOSFET、LDR、LED、太阳能电池、热敏电阻、压敏电阻、变压器、开关、继电器等
基础电子学 - 霍尔效应
霍尔效应以其发现者埃德温·霍尔的名字命名。这有点类似于弗莱明右手定则。当载流导体I置于横向磁场B中时,导体中会感应出垂直于I和B 的电场E。这种现象称为霍尔效应。
解释
当载流导体放置在横向磁场中时,该磁场会对电子施加一定的压力,电子会沿着弯曲的路径继续其旅程。施加能量的导体如下图所示。还指示了磁场。

当电子穿过位于磁场 B 中的导体时,电子将受到磁力。这种磁力将导致电子移动到一侧而不是另一侧。这会在一侧产生负电荷,在另一侧产生正电荷,如下图所示。

这种电荷分离将产生电压差,称为霍尔电压或霍尔电动势。电压不断增加,直到电场在电荷上产生与磁力大小相等且方向相反的电力。这种效应称为霍尔效应。

$$\overrightarrow{F_{磁}}\:\:=\:\:\overrightarrow{F_{电}}\:\:=\:\:q\:\:\overrightarrow{V_{D}}\ :\:\overrightarrow{B}\:\:=\:\:q\:\:\overrightarrow{E_{H}}$$
V D是每个电子经历的速度
$\overrightarrow{E_{H}}\:\:=\:\:\overrightarrow{V_{D}}\:\:\overrightarrow{B}\:\:$因为 V = Ed
其中 q = 电荷量
$\overrightarrow{B}$ = 磁场
$\overrightarrow{V_{D}}$ = 漂移速度
$\overrightarrow{E_{H}}$ = 霍尔电效应
d = 导体平面之间的距离(导体的宽度)
$$V_{H}\:\:=\:\:\varepsilon_{H}\:\:=\:\:\overrightarrow{E_{H}}\:\:d\:\:=\:\ :\overrightarrow{V_{D}}\:\:\overrightarrow{B}\:\:d$$
$$\varepsilon_{H}\:\:=\:\:\overrightarrow{V_{D}}\:\:\overrightarrow{B}\:\:d$$
这是霍尔电动势
用途
霍尔效应用于获取有关半导体类型、载流子符号的信息,以测量电子或空穴浓度和迁移率。由此,我们还可以知道该材料是导体、绝缘体还是半导体。它还用于测量电磁波中的磁通密度和功率。
电流类型
谈到半导体中的电流类型,有两个术语需要讨论。它们是扩散电流和漂移电流。
扩散电流
掺杂完成后,电子和空穴的浓度会出现差异。这些电子和空穴倾向于从电荷密度较高的浓度扩散到浓度较低的水平。由于这些是电荷载流子,因此它们构成称为扩散电流的电流。
为了详细了解这一点,让我们考虑 N 型材料和 P 型材料。
N型材料以电子为多数载流子,以少量空穴为少数载流子。
P型材料以空穴作为多数载流子,以少量电子作为少数载流子。
如果这两种材料彼此太靠近而无法连接,则来自 N 型材料价带的少量电子倾向于向 P 型材料移动,而来自 P 型材料价带的少量空穴倾向于向 P 型材料移动。 N型材料。这两种材料之间发生扩散的区域称为耗尽区。

因此,在不施加任何外部能量的情况下,由于这些电子和空穴的扩散而形成的电流可以称为扩散电流。
漂移电流
由于施加电场而导致带电粒子(电子或空穴)漂移(运动)而形成的电流称为漂移电流。下图解释了漂移电流,无论施加的电场如何,都会产生差异。

电流量取决于所施加的电荷。耗尽区的宽度也会受到该漂移电流的影响。为了使元件在有源电路中发挥作用,漂移电流起着重要作用。
基础电子学 - 电阻器
Resist这个词的意思是“反对”。电阻是导体或半导体中抵抗电子流动的特性。电阻器是一种具有电阻特性的电子元件。
符号和单位
电阻器的符号如下所示。

电阻的单位是欧姆,用Ω(omega)表示。
电阻的公式为
R=V/I
其中V是电压,I是电流。制造具有每个值的电阻器确实很困难。因此,选择的值很少,并且仅制造这种值的电阻器。这些被称为“首选值”。在实践中,选择具有接近值的电阻器来匹配所需的应用。这就是实用电阻器的样子 -

颜色编码
使用称为颜色编码的过程来确定电阻器的电阻值,如上图所示。电阻器涂有四种色带,每种颜色决定特定值。下表显示了每种颜色所表示的值的列表。
| 颜色 | 数字 | 乘数 | 宽容 |
|---|---|---|---|
| 黑色的 | 0 | 10 0 = 1 | |
| 棕色的 | 1 | 10 1 = 10 | 1 |
| 红色的 | 2 | 10 2 = 100 | 2 |
| 橙子 | 3 | 10 3 = 1000 | |
| 黄色的 | 4 | 10 4 = 10000 | |
| 绿色的 | 5 | 10 5 = 100000 | 0.5 |
| 蓝色的 | 6 | 10 6 = 1000000 | 0.25 |
| 紫色 | 7 | 10 7 = 10000000 | 0.1 |
| 灰色的 | 8 | 10 8 = 100000000 | |
| 白色的 | 9 | 10 9 = 1000000000 | |
| 金子 | 10 -1 = 0.1 | 5 | |
| 银 | 10 -2 = 0.01 | 10 | |
| (没有任何) | 20 |
前两个色带表示值的第一个和第二个数字,第三个色带表示乘数(添加的零数)。第四色带表示公差值。
容差是电阻器可以承受而不被损坏的值范围。这是一个重要因素。下图显示了如何通过颜色代码确定电阻器的值。

五色带电阻器的公差为 2% 和 1%,也适用于其他高精度电阻器。在这五环电阻中,前三环代表数字,第四环代表乘数,第五环代表容差。
让我们看一个例子来了解颜色编码过程。
示例 1 - 确定颜色代码为黄色、蓝色、橙色和银色的电阻器的值。
解决方案- 黄色的值为 4,蓝色为 6,橙色为 3,代表乘数。银是±10,这是公差值。
因此电阻值为 46×10 3 = 46kΩ
该电阻的最大阻值是
46kΩ 或 46000Ω + 10% = 46000 + 4600 = 50600Ω = 50.6kΩ
该电阻的最小阻值是
46kΩ 或 46000Ω - 10% = 46000 - 4600 = 41400Ω = 41.4kΩ
在了解了有关电阻器的不同细节之后,我们需要学习一些术语。此外,我们还必须处理几种连接类型的电阻器的不同Behave。
重要条款
在讨论我们拥有的电阻器类型之前,我们需要讨论一些术语。人们需要在这一阶段了解这些术语,并随着我们的进一步进展才能理解它们。
反抗
电阻是电阻器阻止电流流动的特性。当交流电通过电阻时,会产生与电流同相的电压降。
指示 - R
单位 -欧姆
符号 - Ω
除了电阻之外,还有其他重要术语,称为电抗和阻抗。
电抗
由于电路中存在电容和电感而对交流电提供的电阻可以理解为电抗。当交流电通过纯电抗时,会产生与电流异相 90° 的电压降。
根据相位,即+90°或-90°,电抗可以称为感抗或容抗。
指示 - X
单位 -欧姆
符号 - Ω
阻抗
阻抗是欧姆电阻和电抗综合作用产生的对交流电的有效阻力。当交流电通过阻抗时,会产生与电流异相 0° 到 90° 之间的电压降。
指示 - I
单位 -欧姆
符号 - Ω
电导
这是材料的导电能力。它是阻力的倒数。
指示 - G
单位 -莫斯
符号 - ℧
电阻器中的电路连接
连接在电路中时的电阻器,该连接可以是串联或并联。现在让我们知道如果它们串联连接、并联连接时,总电流、电压和电阻值会发生什么变化。
串联电阻
让我们观察一下当几个电阻串联时会发生什么。让我们考虑三个不同值的电阻,如下图所示。

反抗
具有串联电阻的电路的总电阻等于各个电阻的总和。这意味着,上图中有三个电阻,其阻值分别为 1KΩ、5KΩ 和 9KΩ。
电阻网络的总电阻值为 -
$$R\:\:=\:\:R_{1}\:+\:R_{2}\:+\:R_{3}$$
这意味着 1 + 5 + 9 = 15KΩ 是总电阻。
其中,R 1是上述电阻网络中第一个电阻的阻值,R 2是第二个电阻的阻值,R 3是第三个电阻的阻值。
电压
串联电阻网络上出现的总电压是每个单独电阻上的压降之和。在上图中,我们有三个不同的电阻,每级都有三个不同的压降值。
电路中出现的总电压 -
$$V\:\:=\:\:V_{1}\:+\:V_{2}\:+\:V_{3}$$
这意味着 1v + 5v + 9v = 15v 是总电压。
其中,V 1是上述电阻网络中第一个电阻的压降,V 2是第二个电阻的压降,V 3是第三个电阻的压降。
当前的
流经一组串联电阻的电流总量在整个电阻网络的所有点上都是相同的。因此,在输入端或电阻器之间的任意点甚至输出端测量时,电流均为 5A。
当前通过网络 -
$$I\:\:=\:\:I_{1}\:=\:I_{2}\:=\:I_{3}$$
这意味着所有点的电流均为 5A。
其中,I 1是通过上述电阻网络中的第一个电阻的电流,I 2是通过第二个电阻的电流,I 3是通过上述电阻网络中的第三个电阻的电流。
并联电阻
让我们观察一下当几个电阻并联时会发生什么。让我们考虑三个不同值的电阻,如下图所示。

反抗
具有并联电阻器的电路的总电阻的计算方式与串联电阻器网络方法不同。此处,将各个电阻的倒数 (1/R) 值与代数和的倒数相加即可得到总电阻值。
电阻网络的总电阻值为 -
$$\frac{1}{R}\:\:=\:\:\frac{1}{R_{1}}\:\:+\:\:\frac{1}{R_{2}} \:\:+\frac{1}{R_{3}}$$
其中,R 1是上述电阻网络中第一个电阻的阻值,R 2是第二个电阻的阻值,R 3是第三个电阻的阻值。
例如,如果考虑前面示例的电阻值,则意味着R 1 = 1KΩ、R 2 = 5KΩ以及R 3 = 9KΩ。并联电阻网络的总电阻为 -
$$\frac{1}{R}\:\:=\:\:\frac{1}{1}\:\:+\:\:\frac{1}{5}\:\:+\压裂{1}{9}$$
$$=\:\:\frac{45\:\:+\:\:9\:\:+\:\:5}{45}\:\:=\:\:\frac{59}{ 45}$$
$$R\:\:=\:\:\frac{45}{59}\:\:=\:\:0.762K\Omega\:\:=\:\:76.2\Omega$$
根据计算并联电阻的方法,我们可以推导出两个电阻并联网络的简单方程。它是 -
$$R\:\:=\:\:\frac{R_{1}\:\:\times\:\:R_{2}}{R_{1}\:\:+\:\:R_{ 2}}\:$$
电压
并联电阻网络上出现的总电压与每个单独电阻上的电压降相同。
电路中出现的电压 -
$$V\:\:=\:\:V_{1}\:=\:V_{2}\:=\:V_{3}$$
其中,V 1是上述电阻网络中第一个电阻的压降,V 2是第二个电阻的压降,V 3是第三个电阻的压降。因此,并联电阻网络的所有点上的电压都是相同的。
当前的
进入并联电阻网络的电流总量是所有并联支路中流动的所有单独电流的总和。每个支路的电阻值决定了流过它的电流值。通过网络的总电流为
$$I\:\:=\:\:I_{1}\:+\:I_{2}\:+\:I_{3}$$
其中,I 1是通过上述电阻网络中的第一个电阻的电流,I 2是通过第二个电阻的电流,I 3是通过上述电阻网络中的第三个电阻的电流。因此,不同支路中的各个电流之和就获得了并联电阻网络中的总电流。
电阻器特别用作许多电路输出中的负载。如果根本不使用电阻负载,则在负载之前放置一个电阻器。电阻器通常是任何电路中的基本元件。
基础电子学 - 非线性电阻器
根据所用材料的类型、制造过程及其应用,电阻器有多种类型。分类如下图所示。

线性电阻器具有线性VI特性,非线性电阻器具有非线性VI特性。非线性电阻器是电压和电流特性非线性变化的电阻器。电压和电流值根据温度和光线等其他因素而变化,但它们可能不是线性的。
热敏电阻
热是指温度。在该电阻器中,电阻随温度变化。如果热量增加,电阻就会减小,反之亦然。这用于测量和控制目的。
热敏电阻的主要类型有NTC和PTC。
NTC 是负温度系数,在此类器件中,电阻随着温度升高而减小。它们用于保护设备免受过压情况的影响。
PTC 是正温度系数,在此类设备中,电阻随着温度的升高而增加。它们用于保护设备免受过流情况的影响。
下图显示了 NTC 热敏电阻及其符号。

光敏电阻
照片意味着光。在该电阻器中,电阻随光而变化。随着光的增加,电阻减小,反之亦然。这也用于测量和控制目的。也称为LDR(光敏电阻)

压敏电阻
压敏电阻的电阻随施加的电压而变化。当电压增加时,电阻减小;如果电压减小,电阻增加。它也称为VDR(电压相关电阻器)。

表面贴装
自从表面贴装技术引入以来,这些技术得到了广泛的应用。这些可以称为片式电阻器,这意味着集成在陶瓷芯片上的电阻层。
与普通电阻器相比,这些表面贴装电阻器非常小,因此占用的空间较小。它们有效且散热较少。这些电阻器的发明改变了 PCB(印刷电路板)的外观并大大减小了其尺寸。
表面贴装电阻器的优点是 -
- 这些尺寸紧凑。
- 这些都是非常稳定的。
- 他们有很好的宽容度。
- 它们可有效减少热量耗散。
下图显示了表面贴装电阻器的图像。

基础电子学 - 线性电阻
线性电阻器是一种电阻不随流过它的电流而变化的电阻器。通过它的电流始终与施加在其上的电压成正比。线性电阻器又分为固定电阻器和可变电阻器。
可变电阻器
可变电阻器是指可以根据需要手动改变阻值的电阻器。借助连接的轴,从一系列电阻值中选择特定的电阻值。可变电阻器的符号如下所示。
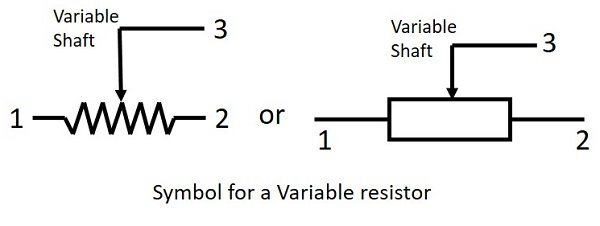
借助我们的分类,可以更好地理解这些电阻器。可变电阻又分为电位器、变阻器和微调器。
电位器
电位器简称为Pot。这是一个具有滑动或旋转轴的三端电阻器。该轴在操作时形成可调分压器。下图显示了电位计的图像。
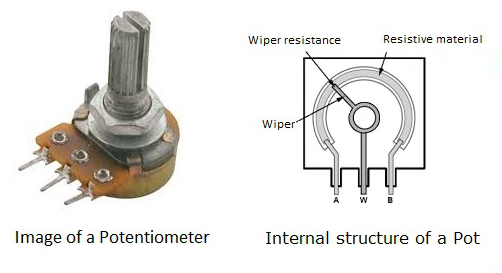
电位计还测量电路中的电位差(电压)。内部铺设一条电阻值从低到高的电阻材料路径,并放置游标,以便将电阻材料连接到电路。这主要用作电视机和音乐系统中的音量控制器。
变阻器
变阻器可以简称为线绕电阻器。电阻丝紧紧缠绕在绝缘陶瓷芯上。雨刮器在这些绕组上滑动。一个连接连接到电阻线的一端,第二个连接连接到电刷或滑动触点,以获得所需的电阻。
变阻器用于控制电流。这些主要用于重型电机的速度控制。由此获得的电阻为千欧姆量级。变阻器大多有单管变阻器和双管变阻器,如下图所示。

作为可变电阻,它们通常用于电路中的调谐和校准。如今,变阻器的使用已被开关电子设备取代,因为变阻器的效率较低。
修剪器
微调器既是可变电阻器又是电位器(测量电位差)。该微调电位器简称为Trim Pot。如果这些用作可变电阻器,则它们被称为预设电阻器。

这些微调电位计有不同类型,例如单圈或多圈。这些是用于调谐和校准的小型可变电阻器。它们的寿命比其他可变电阻器短。
基础电子学 - 固定电阻器
固定电阻器是线性电阻器的一种。如果电阻器的值是固定的,则该电阻器被称为固定电阻器。固定电阻器的值不能像可变电阻器那样改变,因为其值是在制造时确定的。下图表示固定电阻器的符号。

固定电阻器根据其制造工艺和制造中使用的材料分为不同类型。分类如下。

碳成分
碳成分电阻器是碳颗粒、石墨和陶瓷粉末与粘土等粘合剂物质的混合物。该混合物经过高压和高温处理。将整个部件模制在外壳中后,将固定引线。
碳成分电阻器的热质量较高,以承受高能量脉冲。
这些电阻器的缺点是稳定性低且噪声高。
下图显示了碳质电阻器的图像。

碳复合电阻器用于浪涌保护、限流和高压电源。
线绕
线绕电阻器是通过将由电阻材料制成的线缠绕在磁芯上而形成的。金属芯充当非导电材料,而电阻线则导电,但具有一定的电阻。线绕电阻器的图像如下所示。

通常使用镍铬合金线或锰铜线来缠绕磁芯,因为它们具有高电阻。而塑料、陶瓷或玻璃则用于核心。
- 线绕电阻器非常精确。
- 它们在低电阻值和高额定功率方面表现出色。
这些是最古老的固定电阻器类型,但至今仍在使用。
厚膜
薄膜电阻器在陶瓷基底上有一个电阻层,其厚度决定了它们所属的类型。厚膜电阻器上的电阻层厚度比薄膜电阻器厚得多。厚膜电阻器是通过将特殊浆料(玻璃和金属氧化物的混合物)烧制到基板上来生产的。
厚膜电阻器主要分为三种类型:熔断电阻器、金属陶瓷膜电阻器和金属氧化物膜电阻器。
熔断电阻器
可熔电阻器类似于线绕电阻器。但这些电阻器除了提供电阻之外,还充当保险丝。熔断电阻的图像如下所示。

在该电阻器中,电流流过靠近电阻器主体放置的弹簧加载连接。附着在电阻器弹簧线上的斑点吸收电阻器因电流而产生的热量。如果热量增加,斑点上的附件就会熔化并打开连接。

因此我们可以说,这些电阻器限制了电流,但如果电路的额定功率超过指定值,这些电阻器就会充当保险丝来打开或断开电路。这些电阻器的阻值通常小于 10 欧姆。这些电阻器通常用于电视机、放大器和其他昂贵的电子电路中。
金属陶瓷薄膜电阻器
金属陶瓷薄膜电阻器是由一种称为金属陶瓷的特殊材料制成的薄膜电阻器。金属陶瓷是由陶瓷和金属结合而成的复合合金。这种组合提供了这两种材料的优点,例如陶瓷的耐高温和耐磨性以及金属的柔韧性和导电性。

金属薄膜层包裹在电阻材料周围并固定在陶瓷金属或金属陶瓷基板中。固定在 PCB 上时,采用引线以便于连接。它们具有高稳定性,因为温度不会影响其性能。
金属氧化膜电阻器
金属氧化膜电阻器是通过在作为基板的加热玻璃棒上氧化厚厚的氯化锡膜而形成的。它们具有高温稳定性,可在高电压下使用。这些电阻器具有低工作噪声。

金属氧化膜电阻器与金属膜电阻器的区别仅在于镀膜类型。金属氧化物是一种金属化合物,如锡与氧形成氧化锡,氧化锡以薄膜形式涂在电阻器上。该电阻器的电阻率取决于添加到氧化锡中的氧化锑的量。
薄膜
薄膜电阻器在陶瓷基底上有一个宽度为 0.1 微米或更小的电阻层。薄膜电阻器具有真空沉积在绝缘基板上的金属膜。
薄膜电阻精度更高,温度系数更好,更稳定。薄膜电阻器进一步分为两种类型,例如 -
- 碳膜电阻器
- 金属膜电阻器
碳膜电阻
碳膜电阻器是通过在陶瓷基板上沉积碳膜层而制成的。碳膜充当电流的电阻材料,陶瓷物质充当绝缘物质。两端固定金属帽,引出铜引线。
下图显示了碳膜电阻器的结构。

这些电阻器的主要优点是稳定性高、工作范围宽、噪声低、成本低。与碳复合电阻器相比,碳膜电阻器由于其低噪声而成为最优选的电阻器。
金属膜电阻器
薄膜涂层决定了金属氧化膜电阻器和金属膜电阻器的区别。金属膜电阻器中,使用诸如镍铬之类的金属物质薄膜来涂覆电阻器,而在金属氧化物电阻器中,则使用诸如氧化锡之类的金属氧化物膜来涂覆电阻器。

金属膜电阻器的电阻温度系数低,这意味着电阻值受温度的影响较小。
瓦数
使用电阻器时,如果电流增加,电阻器会散发一些热量。如果该值超过某个临界值,电阻器可能会损坏。为了避免这种情况,电阻器的额定功率印在一些更高值的电阻器上。
瓦数是以瓦特表示的电功率。电功率是电能的传输速率。
功率P = VI = I 2 R
基础电子产品 - 电容器
电容器是一种无源元件,能够以极板之间的电势差形式存储能量。它可以抵抗电压的突然变化。电荷以两块板之间电势差的形式存储,根据电荷存储的方向形成正电势差和负电势差。
这两个板之间存在一个非导电区域,称为电介质。这种电介质可以是真空、空气、云母、纸、陶瓷、铝等。电容器的名称由所使用的电介质给出。
符号和单位
电容的标准单位是法拉。一般来说,可用的电容器的值将是微法拉、皮法拉和纳法拉的量级。电容器的符号如下所示。

电容器的电容与极板之间的距离成正比,与极板的面积成反比。此外,材料的介电常数越高,电容就越高。介质的介电常数描述了该介质中每单位电荷产生的电通量。下图显示了一些实用的电容器。

当具有相同面积 A 和相等宽度的两个板彼此平行放置且间隔距离 d 时,如果向板施加一些能量,则该平行板电容器的电容可称为 -
$$C\:\:=\:\:\frac{\varepsilon_{0}\:\:\varepsilon_{r}\:\:d}{A}$$
在哪里
C = 电容器的电容
$\varepsilon_{0}$ = 自由空间的介电常数
$\varepsilon_{r}$ = 介电介质的介电常数
d = 板之间的距离
A = 两个导电板的面积

施加一些电压后,电荷沉积在电容器的两个平行板上。这种电荷沉积缓慢发生,当电容器两端的电压等于施加的电压时,充电停止,因为进入的电压等于离开的电压。
充电速率取决于电容值。电容值越大,极板中电压的变化率越慢。
电容器的工作
电容器可以理解为储存电能的两端无源元件。该电能存储在静电场中。
最初,电容器两个极板上的负电荷和正电荷处于平衡状态。电容器没有充电或放电的趋势。负电荷是由电子积累形成的,而正电荷是由电子耗尽形成的。由于这种情况在没有任何外部电荷的情况下发生,因此这种状态是静电状态。下图显示了带静电荷的电容器。

根据交流电源正负周期变化的电子积累和消耗,可以理解为“电流”。这称为位移电流。由于这是交流电,因此电流的方向不断变化。
电容器充电
当给出外部电压时,电荷转换成静电荷。这种情况发生在电容器充电时。电源的正电势吸引来自电容器正极板的电子,使其变得更正。而电源的负电势迫使电子到达电容器的负极板,使其更加负电。下图解释了这一点。

在充电过程中,电子通过直流电源移动,但不通过作为绝缘体的电介质。当电容器开始充电时,该位移很大,但随着充电而减小。当电容器两端的电压等于电源电压时,电容器停止充电。

让我们看看当电容器开始充电时电介质会发生什么变化。
介电Behave
当电荷沉积在电容器极板上时,就会形成静电场。该静电场的强度取决于板上电荷的大小和介电材料的介电常数。介电常数是衡量电介质是否允许静电线穿过多远的指标。
电介质实际上是绝缘体。它的电子位于Atomics的最外层轨道。让我们观察一下他们是如何受到影响的。当极板上不带电荷时,电介质中的电子沿圆形轨道运动。如下图所示。

当发生电荷沉积时,电子倾向于向带正电的板移动,但它们仍然继续旋转,如图所示。

如果电荷进一步增加,轨道就会扩大更多。但如果它仍然增加,电介质就会击穿,使电容器短路。现在,电容器已充满电,可以放电了。如果我们为它们提供从负极板到正极板的路径就足够了。电子在没有任何外部供应的情况下流动,因为一侧有太多电子,而另一侧几乎没有电子。这种不平衡是通过电容器的放电来调节的。
此外,当找到放电路径时,介电材料中的Atomics往往会进入其正常的圆形轨道,从而迫使电子放电。这种放电使电容器能够在短时间内提供高电流,就像相机闪光灯一样。
颜色编码
要知道电容器的值,通常标记如下 -
n35 = 0.35nF 或 3n5 = 3.5nF 或 35n = 35nF 等等。
有时标记会像 100K,这意味着 k = 1000pF。那么该值将为 100 × 1000pF = 100nF。
尽管现在正在使用这些数字标记,但很久以前就开发了国际颜色编码方案,以了解电容器的值。颜色编码指示如下所示。
| 表带颜色 | 数字 A 和 B | 乘数 | 公差 (t) > 10pf | 公差 (t) < 10pf | 温度系数 |
|---|---|---|---|---|---|
| 黑色的 | 0 | × 1 | ±20% | ±2.0pF | |
| 棕色的 | 1 | × 10 | ±1% | ±0.1pF | -33×10 -6 |
| 红色的 | 2 | × 100 | ±2% | ±0.25pF | -75×10 -6 |
| 橙子 | 3 | × 1,000 | ±3% | -150×10 -6 | |
| 黄色的 | 4 | × 10,000 | ±4% | -220×10 -6 | |
| 绿色的 | 5 | × 100,000 | ±5% | ±0.5pF | -330×10 -6 |
| 蓝色的 | 6 | × 1,000000 | -470×10 -6 | ||
| 紫色 | 7 | -750×10 -6 | |||
| 灰色的 | 8 | × 0.01 | +80%, -20% | ||
| 白色的 | 9 | × 0.1 | ±10% | ±1.0pF | |
| 金子 | × 0.1 | ±5% | |||
| 银 | × 0.01 | ±10% |
这些指示用于识别电容器的值。

在这五环电容器中,前两环代表数字,第三环代表乘数,第四环代表容差,第五环代表电压。让我们看一个例子来了解颜色编码过程。
示例 1 - 确定颜色代码为黄色、紫色、橙色、白色和红色的电容器的值。
解决方案- 黄色的值为 4,紫色为 7,橙色为 3,代表乘数。白色为±10,这是公差值。红色代表电压。但要知道额定电压,我们有另一个表,必须从该表中知道该电容器所属的特定频带。
因此电容值为 47nF,10% 250v(V 频段电压)
下表显示了如何根据电容器所属的频段确定电压。
| 表带颜色 | 额定电压 (V) | ||||
|---|---|---|---|---|---|
| J型 | K型 | L型 | M型 | N型 | |
| 黑色的 | 4 | 100 | 10 | 10 | |
| 棕色的 | 6 | 200 | 100 | 1.6 | |
| 红色的 | 10 | 300 | 250 | 4 | 35 |
| 橙子 | 15 | 400 | 40 | ||
| 黄色的 | 20 | 500 | 400 | 6.3 | 6 |
| 绿色的 | 25 | 600 | 16 | 15 | |
| 蓝色的 | |||||