交流电桥
在本章中,我们将讨论可用于测量电感的交流电桥。交流电桥仅使用交流电压信号工作。交流电桥的电路图如下图所示。
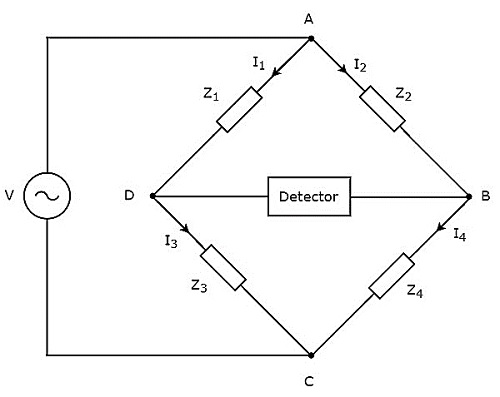
如上图所示,交流电桥主要由四个桥臂组成,四个桥臂连接成菱形或方形。所有这些臂都包含一些阻抗。
为了找到未知阻抗的值,还需要检测器和交流电压源。因此,这两者之一放置在交流电桥的一个对角线上,另一个放置在交流电桥的另一对角线上。惠斯通电桥的平衡条件为 -
$$R_{4}=\frac{R_{2}R_{3}}{R_{1}}$$
只需将上式中的R换成Z即可得到交流电桥的平衡条件。
$$Z_{4}=\frac{Z_{2}Z_{3}}{Z_{1}}$$
$\右箭头Z_{1}Z_{4}=Z_{2}Z_{3}$
这里,$Z_{1}$和$Z_{2}$是固定阻抗。而 $Z_{3}$ 是标准可变阻抗,$Z_{4}$ 是未知阻抗。
注- 我们可以根据应用选择这四个阻抗中的任意两个作为固定阻抗,一个阻抗作为标准可变阻抗,另一个阻抗作为未知阻抗。
以下是两个交流电桥,可用于测量电感。
- 麦克斯韦桥
- 海斯桥
现在,让我们一一讨论这两种交流电桥。
麦克斯韦桥
麦克斯韦电桥是一种具有四个臂的交流电桥,四个臂以菱形或方形的形式连接。该电桥的两个臂由单个电阻器组成,一个臂由电阻器和电感器的串联组合组成,另一臂由电阻器和电容器的并联组合组成。
使用交流检测器和交流电压源来查找未知阻抗的值。因此,这两者之一放置在麦克斯韦电桥的一条对角线上,另一个放置在麦克斯韦电桥的另一对角线上。
麦克斯韦电桥用于测量介质电感值。麦克斯韦电桥的电路图如下图所示。
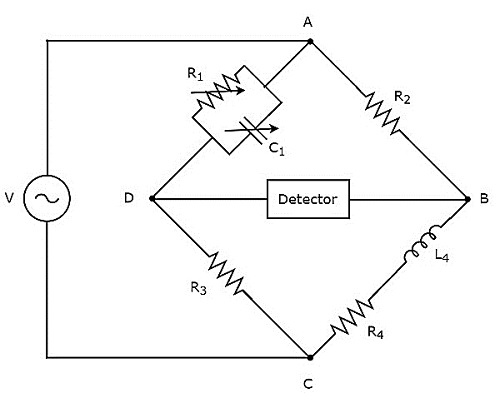
在上述电路中,臂AB、BC、CD和DA一起形成菱形或正方形。AB 臂和 CD 臂分别由电阻 $R_{2}$ 和 $R_{3}$ 组成。臂 BC 由电阻器 $R_{4}$ 和电感器 $L_{4}$ 的串联组合组成。DA 臂由电阻器 $R_{1}$ 和电容器 $C_{1}$ 并联组合组成。
令$Z_{1}、Z_{2}、Z_{3}$和$Z_{4}$分别为DA、AB、CD和BC臂的阻抗。这些阻抗的值将是
$$Z_{1}=\frac{R_{1}\left (\frac{1}{j\omega C_{1}} \right )}{R_{1}+\frac{1}{j\omega C_{1}}}$$
$$\Rightarrow Z_{1}=\frac{R_{1}}{1+j \omega R_{1}C_{1}}$$
$Z_{2}=R_{2}$
$Z_{3}=R_{3}$
$Z_{4}=R_{4}+j \omega L_{4}$
将这些阻抗值代入以下交流电桥的平衡条件中。
$$Z_{4}=\frac{Z_{2}Z_{3}}{Z_{1}}$$
$$R_{4}+j\omega L_{4}=\frac{R_{2}R_{3}}{\left ( {\frac{R_{1}}{1+j \omega R_{1} C_{1}}} \右)}$$
$\Rightarrow R_{4}+j\omega L_{4}=\frac{R_{2}R_{3}\left (1+j \omega R_{1}C_{1} \right )}{R_{ 1}}$
$\Rightarrow R_{4}+j\omega L_{4}=\frac{R_{2}R_{3}}{R_{1}}+\frac{j \omega R_{1}C_{1}R_ {2}R_{3}}{R_{1}}$
$\R_{4}+j\omega L_{4}=\frac{R_{2}R_{3}}{R_{1}}+j \omega C_{1}R_{2}R_{3} $
通过比较上式各自的实部和虚部,我们可以得到
$R_{4}=\frac{R_{2}R_{3}}{R_{1}}$方程1
$L_{4}=C_{1}R_{2}R_{3}$公式 2
通过将电阻器 $R_{1}$、$R_{2}$ 和 $R_{3}$ 的值代入公式 1,我们将得到电阻器的值 $R_{4}$。同样,通过将电容器的值 $C_{1}$ 以及电阻器的值 $R_{2}$ 和 $R_{3}$ 代入等式 2,我们将得到电感器的值 $L_{4 }$。
麦克斯韦电桥的优点是电阻器 $ R_ {4}$ 和电感器 $L_{4}$ 的值都与频率值无关。
海斯桥
海氏电桥是麦克斯韦电桥的修改版,我们通过将由电阻和电容的并联组合组成的臂修改为麦克斯韦电桥中电阻和电容的串联组合组成的臂来得到。
海氏电桥用于测量高电感值。海氏电桥的电路图如下图所示。
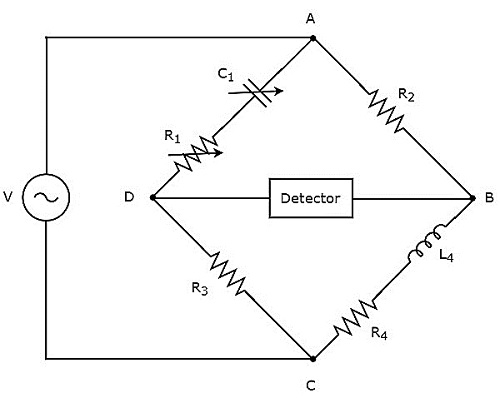
在上述电路中,臂AB、BC、CD和DA一起形成菱形或正方形。AB 和 CD 臂分别由电阻 $R_{2}$ 和 $R_{3}$ 组成。臂 BC 由电阻器 $R_{4}$ 和电感器 $L_{4}$ 的串联组合组成。DA 臂由电阻器 $R_{1}$ 和电容器 $C_{1}$ 的串联组合组成。
令$Z_{1}、Z_{2}、Z_{3}$和$Z_{4}$分别为DA、AB、CD和BC臂的阻抗。这些阻抗的值将是
$$Z_{1}=R_{1}+\frac{1}{j \omega C_{1}}$$
$\Rightarrow Z_{1}=\frac{1+j \omega R_{1}C_{1}}{j \omega C_{1}}$
$Z_{2}=R_{2}$
$Z_{3}=R_{3}$
$Z_{4}=R_{4}+j \omega L_{4}$
将这些阻抗值代入以下交流电桥的平衡条件中。
$$Z_{4}=\frac{Z_{2}Z_{3}}{Z_{1}}$$
$R_{4}+j \omega L_{4}=\frac{R_{2}R_{3}}{\left ( \frac{1+j \omega R_{1}C_{1}}{j \欧米茄 C_{1}}\右)}$
$R_{4}+j \omega L_{4}=\frac{R_{2}R_{3}j \omega C_{1}}{\left ( 1+j \omega R_{1}C_{1} \右)}$
将上式右侧项的分子和分母乘以 $1 - j \omega R_{1}C_{1}$。
$\Rightarrow R_{4}+j \omega L_{4}=\frac{R_{2}R_{3}j \omega C_{1}}{\left ( 1+j \omega R_{1}C_{ 1}\right )}\times \frac{\left (1 - j \omega R_{1}C_{1} \right )}{\left (1 - j \omega R_{1}C_{1} \right )}$
$\Rightarrow R_{4}+j \omega L_{4}=\frac{\omega^{2}{C_{1}}^{2}R_{1}R_{2}R_{3}+j \欧米伽 R_{2}R_{3}C_{1}}{\left ( 1+\omega^{2}{R_{1}}^{2}{C_{1}}^{2}\right )} $
通过比较上式各自的实部和虚部,我们可以得到
$R_{4}= \frac{\omega^{2}{C_{1}}^{2}R_{1}R_{2}R_{3}}{\left ( 1+\omega^{2} {R_{1}}^{2}{C_{1}}^{2}\right )}$公式 3
$L_{4}= \frac{R_{2}R_{3}C_{1}}{\left ( 1+\omega^{2}{R_{1}}^{2}{C_{1}} ^{2}\right )}$方程 4
将 $R_{1}、R_{2}、R_{3}、C_{1}$ 和 $\omega$ 的值代入公式 3 和公式 4 中,我们将得到电阻值 $R_{4 }$ 和电感器,$L_{4}$。
