数据结构与算法-队列

队列和栈一样，也是一种抽象的数据结构。队列与堆栈的不同之处在于队列的两端都是开放的。因此，它遵循 FIFO（先进先出）结构，即先插入的数据项也将首先被访问。数据通过一端插入队列，并使用另一端从队列中删除。

车

现实世界中队列的示例可以是单车道单向道路，其中车辆先进入，先退出。更多现实世界的例子可以看作是售票窗口和公交车站的排队。

队列的表示

与堆栈ADT类似，队列ADT也​​可以使用数组、链表或指针来实现。作为本教程中的一个小示例，我们使用一维数组实现队列。

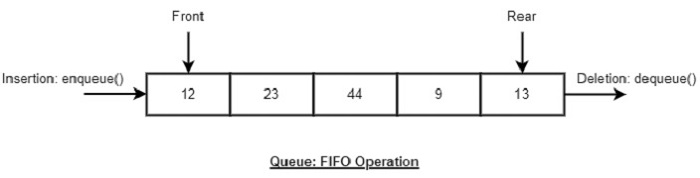
队列的表示

基本操作

队列操作还包括队列的初始化、使用以及从内存中永久删除数据。

队列ADT中最基本的操作包括：enqueue()、dequeue()、peek()、isFull()、isEmpty()。这些都是用于执行数据操作和检查队列状态的内置操作。

队列使用两个指针 - front和after。前指针从前端访问数据（帮助入队），而后指针从后端访问数据（帮助出队）。

插入操作：enqueue()

enqueue ()是一种数据操作操作，用于将元素插入堆栈。下面的算法以更简单的方式描述了 enqueue() 操作。

算法

1 − START
2 – Check if the queue is full.
3 − If the queue is full, produce overflow error and exit.
4 − If the queue is not full, increment rear pointer to point the next empty space.
5 − Add data element to the queue location, where the rear is pointing.
6 − return success.
7 – END

例子

以下是此操作在各种编程语言中的实现 -

C C++ Java Python 
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isFull(){
   return itemCount == MAX;
}
bool isEmpty(){
   return itemCount == 0;
}
int removeData(){
   int data = intArray[front++];
   if(front == MAX) {
      front = 0;
   }
   itemCount--;
   return data;
}
void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
int main(){
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);
   insert(15);
   printf("Queue: ");
   while(!isEmpty()) {
      int n = removeData();
      printf("%d ",n);
   }
}

输出

Queue: 3 5 9 1 12 15

#include <iostream>
#include <string>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isFull(){
   return itemCount == MAX;
}
bool isEmpty(){
   return itemCount == 0;
}
int removeData(){
   int data = intArray[front++];
   if(front == MAX) {
      front = 0;
   }
   itemCount--;
   return data;
}
void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
int main(){
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);
   insert(15);
   printf("Queue: ");
   while(!isEmpty()) {
      int n = removeData();
      printf("%d ",n);
   }
}

输出

Queue: 3 5 9 1 12 15

import java.util.LinkedList;
import java.util.Queue;
public class QueueExample {
   public static void main(String[] args) {
      Queue<Integer> q = new LinkedList<>();
      q.add(6);
      q.add(1);
      q.add(8);
      q.add(4);
      q.add(7);
      System.out.println("The queue is: " + q);
   }
}

输出

The queue is: [6, 1, 8, 4, 7]

class Queue:
   def __init__(self):
      self.queue = list()
   def __str__(self):
      return str(self.queue)
   def addtoqueue(self,data):

   # Insert method to add element
      if data not in self.queue:
         self.queue.insert(0,data)
         return True
      return False

q = Queue()
q.addtoqueue("36")
q.addtoqueue("24")
q.addtoqueue("48")
q.addtoqueue("12")
q.addtoqueue("66")
print("Queue:")
print(q)

输出

Queue:
['66', '12', '48', '24', '36']

删除操作：dequeue()

dequeue ()是一种数据操作操作，用于从堆栈中删除元素。下面的算法以更简单的方式描述了 dequeue() 操作。

算法

1 – START
2 − Check if the queue is empty.
3 − If the queue is empty, produce underflow error and exit.
4 − If the queue is not empty, access the data where front is pointing.
5 − Increment front pointer to point to the next available data element.
6 − Return success.
7 – END

例子

以下是此操作在各种编程语言中的实现 -

C C++ Java Python 
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isFull(){
   return itemCount == MAX;
}
bool isEmpty(){
   return itemCount == 0;
}
void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
int removeData(){
   int data = intArray[front++];
   if(front == MAX) {
      front = 0;
   }
   itemCount--;
   return data;
}
int main(){
   int i;
   
   /* insert 5 items */
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);
   insert(15);
   printf("Queue: ");
   for(i = 0; i < MAX; i++)
      printf("%d ", intArray[i]);

   // remove one item
   int num = removeData();
   printf("\nElement removed: %d\n",num);
   printf("Updated Queue: ");
   while(!isEmpty()) {
      int n = removeData();
      printf("%d ",n);
   }
}

输出

Queue: 3 5 9 1 12 15 
Element removed: 3
Updated Queue: 5 9 1 12 15 

#include <iostream>
#include <string>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isFull(){
   return itemCount == MAX;
}
bool isEmpty(){
   return itemCount == 0;
}
void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
int removeData(){
   int data = intArray[front++];
   if(front == MAX) {
      front = 0;
   }
   itemCount--;
   return data;
}
int main(){
   int i;
   
   /* insert 5 items */
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);
   insert(15);
   printf("Queue: ");
   for(i = 0; i < MAX; i++)
      printf("%d ", intArray[i]);
   
   // remove one item
   int num = removeData();
   printf("\nElement removed: %d\n",num);
   printf("Updated Queue: ");
   while(!isEmpty()) {
      int n = removeData();
      printf("%d ",n);
   }
}

输出

Queue: 3 5 9 1 12 15 
Element removed: 3
Updated Queue: 5 9 1 12 15 

import java.util.LinkedList;
import java.util.Queue;
public class QueueExample {
   public static void main(String[] args) {
      Queue<Integer> q = new LinkedList<>();
      q.add(6);
      q.add(1);
      q.add(8);
      q.add(4);
      q.add(7);
      System.out.println("The queue is: " + q);
      int n = q.remove();
      System.out.println("The element deleted is: " + n);
      System.out.println("Queue after deletion: " + q);
   }
}

输出

The queue is: [6, 1, 8, 4, 7]
The element deleted is: 6
Queue after deletion: [1, 8, 4, 7]

class Queue:
   def __init__(self):
      self.queue = list()
   def __str__(self):
      return str(self.queue)
   def addtoqueue(self,data):

   # Insert method to add element
      if data not in self.queue:
         self.queue.insert(0,data)
         return True
      return False
   def removefromqueue(self):
      if len(self.queue)>0:
         return self.queue.pop()
      return ("Queue is empty")

q = Queue()
q.addtoqueue("36")
q.addtoqueue("24")
q.addtoqueue("48")
q.addtoqueue("12")
q.addtoqueue("66")
print("Queue:")
print(q)
print("Element deleted from queue: ",q.removefromqueue())

输出

Queue:
['66', '12', '48', '24', '36']
Element deleted from queue:  36

peek() 操作

peek() 是一个用于检索队列中最前面的元素的操作，而不删除它。该操作用于借助指针来检查队列的状态。

算法

1 – START
2 – Return the element at the front of the queue
3 – END

例子

以下是此操作在各种编程语言中的实现 -

C C++ Java Python 
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
int peek(){
   return intArray[front];
}
bool isFull(){
   return itemCount == MAX;
}
void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
int main(){
   int i;
   
   /* insert 5 items */
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);
   insert(15);
   printf("Queue: ");
   for(i = 0; i < MAX; i++)
      printf("%d ", intArray[i]);
   printf("\nElement at front: %d\n",peek());
}

输出

Queue: 3 5 9 1 12 15 
Element at front: 3

#include <iostream>
#include <string>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
int peek(){
   return intArray[front];
}
bool isFull(){
   return itemCount == MAX;
}
void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
int main(){
   int i;
   /* insert 5 items */
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);
   insert(15);
   printf("Queue: ");
   for(i = 0; i < MAX; i++)
      printf("%d ", intArray[i]);
   printf("\nElement at front: %d\n",peek());
}

输出

Queue: 3 5 9 1 12 15 
Element at front: 3

import java.util.LinkedList;
import java.util.Queue;
public class QueueExample {
   public static void main(String[] args) {
      Queue<Integer> q = new LinkedList<>();
      q.add(6);
      q.add(1);
      q.add(8);
      q.add(4);
      q.add(7);
      System.out.println("The queue is: " + q);
   }
}

输出

The queue is: [6, 1, 8, 4, 7]

class Queue:
   def __init__(self):
      self.queue = list()
   def __str__(self):
      return str(self.queue)
   def addtoqueue(self,data):
   
   # Insert method to add element
      if data not in self.queue:
         self.queue.insert(0,data)
         return True
      return False
   def peek(self):
      return self.queue[-1]

q = Queue()
q.addtoqueue("36")
q.addtoqueue("24")
q.addtoqueue("48")
q.addtoqueue("12")
q.addtoqueue("66")
print("Queue:")
print(q)
print("The frontmost element of the queue: ",q.peek())

输出

Queue:
['66', '12', '48', '24', '36']
The frontmost element of the queue:  36

isFull() 操作

isFull() 操作验证堆栈是否已满。

算法

1 – START
2 – If the count of queue elements equals the queue size, return true
3 – Otherwise, return false
4 – END

例子

以下是此操作在各种编程语言中的实现 -

C C++ Java Python 
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isFull(){
   return itemCount == MAX;
}
void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
int main(){
   int i;
   /* insert 5 items */
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);
   insert(15);
   printf("Queue: ");
   for(i = 0; i < MAX; i++)
      printf("%d ", intArray[i]);
   printf("\n");
   if(isFull()) {
      printf("Queue is full!\n");
   }
}

输出

Queue: 3 5 9 1 12 15 
Queue is full!

#include <iostream>
#include <string>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isFull(){
   return itemCount == MAX;
}
void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
int main(){
   int i;
   
   /* insert 5 items */
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);
   insert(15);
   printf("Queue: ");
   for(i = 0; i < MAX; i++)
      printf("%d ", intArray[i]);
   printf("\n");
   if(isFull()) {
      printf("Queue is full!\n");
   }
}

输出

Queue: 3 5 9 1 12 15 
Queue is full!

import java.io.*;
public class QueueExample {
   private int intArray[];
   private int front;
   private int rear;
   private int itemCount;
   private int MAX;
   QueueExample(int size) {
      intArray = new int[size];
      front = 0;
      rear = -1;
      MAX = size;
      itemCount = 0;
   }
   public boolean isFull() {
      return itemCount == MAX;
   }
   public void insert(int key) {
      if(!isFull()) {
         if(rear == MAX-1) {
            rear = -1;
         }
         intArray[++rear] = key;
         itemCount++;
      }
   }
   public static void main (String[] args) {
      QueueExample q = new QueueExample(5);
      q.insert(1); // inserting 1 in the stack
      q.insert(2);
      q.insert(3);
      q.insert(4);
      q.insert(5);
      System.out.println("Stack Full? " + q.isFull());
   }
}

输出

Stack Full? true

#python code for isFull in Queue
MAX = 6
intArray = [None] * MAX
front = 0
rear = -1
itemCount = 0

def isFull():
    return itemCount == MAX

def insert(data):
    global rear, itemCount
    if not isFull():
        if rear == MAX-1:
            rear = -1
        rear += 1
        intArray[rear] = data
        itemCount += 1
#inserting 5 items into the Queue
insert(3)
insert(5)
insert(9)
insert(1)
insert(12)
insert(15)
print("Queue: ", end="")
for i in range(MAX):
    print(intArray[i], end=" ")
print()
if isFull():
    print("Queue is full!")

输出

Queue: 3 5 9 1 12 15 
Queue is full!

isEmpty() 操作

isEmpty() 操作验证堆栈是否为空。该操作用于借助栈顶指针来检查堆栈的状态。

算法

1 – START
2 – If the count of queue elements equals zero, return true
3 – Otherwise, return false
4 – END

例子

以下是此操作在各种编程语言中的实现 -

C C++ Java Python 
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isEmpty(){
   return itemCount == 0;
}
int main(){
   int i;
   printf("Queue: ");
   for(i = 0; i < MAX; i++)
      printf("%d ", intArray[i]);
   printf("\n");
   if(isEmpty()) {
      printf("Queue is Empty!\n");
   }
}

输出

Queue: 0 0 0 0 0 0 
Queue is Empty!

#include <iostream>
#include <string>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isEmpty(){
   return itemCount == 0;
}
int main(){
   int i;
   printf("Queue: ");
   for(i = 0; i < MAX; i++)
      printf("%d ", intArray[i]);
   printf("\n");
   if(isEmpty()) {
      printf("Queue is Empty!\n");
   }
}

输出

Queue: 0 0 0 0 0 0 
Queue is Empty!

import java.io.*;
public class QueueExample {
   private int intArray[];
   private int front;
   private int rear;
   private int itemCount;
   private int MAX;
   QueueExample(int size) {
      intArray = new int[size];
      front = 0;
      rear = -1;
      MAX = size;
      itemCount = 0;
   }
   public boolean isEmpty() {
      return itemCount == 0;
   }
   public static void main (String[] args) {
      QueueExample q = new QueueExample(5);
      System.out.println("Stack Empty? " + q.isEmpty());
   }
}

输出

Stack Empty? true

#python code for isFull in Queue
MAX = 6
intArray = [None] * MAX
front = 0
rear = -1
itemCount = 0

def isEmpty():
    return itemCount == 0

print("Queue: ", end="")
for i in range(MAX):
    print(intArray[i], end=" ")
print()
if isEmpty():
    print("Queue is empty!")

输出

Queue: None None None None None None 
Queue is empty!

队列的实现

本章使用四种编程语言进行队列数据结构的算法实现。

C C++ Java Python 
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
int peek(){
   return intArray[front];
}
bool isEmpty(){
   return itemCount == 0;
}
bool isFull(){
   return itemCount == MAX;
}
int size(){
   return itemCount;
}
void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
int removeData(){
   int data = intArray[front++];
   if(front == MAX) {
      front = 0;
   }
   itemCount--;
   return data;
}
int main(){
   
   /* insert 5 items */
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);

   // front : 0
   // rear : 4
   // ------------------
   // index : 0 1 2 3 4
   // ------------------
   // queue : 3 5 9 1 12
   insert(15);

   // front : 0
   // rear : 5
   // ---------------------
   // index : 0 1 2 3 4 5
   // ---------------------
   // queue : 3 5 9 1 12 15
   if(isFull()) {
      printf("Queue is full!\n");
   }

   // remove one item
   int num = removeData();
   printf("Element removed: %d\n",num);

   // front : 1
   // rear : 5
   // -------------------
   // index : 1 2 3 4 5
   // -------------------
   // queue : 5 9 1 12 15
   // insert more items
   insert(16);
   
   // front : 1
   // rear : -1
   // ----------------------
   // index : 0 1 2 3 4 5
   // ----------------------
   // queue : 16 5 9 1 12 15
   // As queue is full, elements will not be inserted.
   insert(17);
   insert(18);

   // ----------------------
   // index : 0 1 2 3 4 5
   // ----------------------
   // queue : 16 5 9 1 12 15
   printf("Element at front: %d\n",peek());
   printf("----------------------\n");
   printf("index : 5 4 3 2 1 0\n");
   printf("----------------------\n");
   printf("Queue: ");
   while(!isEmpty()) {
      int n = removeData();
      printf("%d ",n);
   }
}

输出

Queue is full!
Element removed: 3
Element at front: 5
----------------------
index : 5 4 3 2 1 0
----------------------
Queue: 5 9 1 12 15 16 

#include <iostream>
#include <string>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
int peek(){
   return intArray[front];
}
bool isEmpty(){
   return itemCount == 0;
}
bool isFull(){
   return itemCount == MAX;
}
int size(){
   return itemCount;
}
void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
int removeData(){
   int data = intArray[front++];
   if(front == MAX) {
      front = 0;
   }
   itemCount--;
   return data;
}
int main(){
   
   /* insert 5 items */
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);

   // front : 0
   // rear : 4
   // ------------------
   // index : 0 1 2 3 4
   // ------------------
   // queue : 3 5 9 1 12
   insert(15);

   // front : 0
   // rear : 5
   // ---------------------
   // index : 0 1 2 3 4 5
   // ---------------------
   // queue : 3 5 9 1 12 15
   if(isFull()) {
      printf("Queue is full!\n");
   }

   // remove one item
   int num = removeData();
   printf("Element removed: %d\n",num);

   // front : 1
   // rear : 5
   // -------------------
   // index : 1 2 3 4 5
   // -------------------
   // queue : 5 9 1 12 15
   // insert more items
   insert(16);

   // front : 1
   // rear : -1
   // ----------------------
   // index : 0 1 2 3 4 5
   // ----------------------
   // queue : 16 5 9 1 12 15
   // As queue is full, elements will not be inserted.
   insert(17);
   insert(18);

   // ----------------------
   // index : 0 1 2 3 4 5
   // ----------------------
   // queue : 16 5 9 1 12 15
   printf("Element at front: %d\n",peek());
   printf("----------------------\n");
   printf("index : 5 4 3 2 1 0\n");
   printf("----------------------\n");
   printf("Queue: ");
   while(!isEmpty()) {
      int n = removeData();
      printf("%d ",n);
   }
}

输出

Queue is full!
Element removed: 3
Element at front: 5
----------------------
index : 5 4 3 2 1 0
----------------------
Queue: 5 9 1 12 15 16

import java.util.LinkedList;
import java.util.Queue;
public class QueueExample {
   public static void main(String[] args) {
      Queue<Integer> q = new LinkedList<>();
      q.add(6);
      q.add(1);
      q.add(8);
      q.add(4);
      q.add(7);
      System.out.println("The queue is: " + q);
      int n = q.remove();
      System.out.println("The element deleted is: " + n);
      System.out.println("Queue after deletion: " + q);
      int size = q.size();
      System.out.println("Size of the queue is: " + size);
   }
}

输出

The queue is: [6, 1, 8, 4, 7]The element deleted is: 6
Queue after deletion: [1, 8, 4, 7]
Size of the queue is: 4

class Queue:
   def __init__(self):
      self.queue = list()
   def addtoqueue(self,data):

   # Insert method to add element
      if data not in self.queue:
         self.queue.insert(0,data)
         return True
      return False
   def size(self):
      return len(self.queue)
   def removefromqueue(self):
      if len(self.queue)>0:
         return self.queue.pop()
      return ("Queue is empty")

q = Queue()
q.addtoqueue("36")
q.addtoqueue("24")
q.addtoqueue("48")
q.addtoqueue("12")
q.addtoqueue("66")
print("size of the queue: ",q.size())
print("Element deleted from queue: ",q.removefromqueue())
print("size of the queue after deletion: ",q.size())

输出

size of the queue:  5
Element deleted from queue:  36
size of the queue after deletion:  4