数据结构与算法 - 生成树

生成树是图 G 的子集，其中所有顶点都被尽可能少的边数覆盖。因此，生成树没有环，也不能断开。

通过这个定义，我们可以得出结论：每个连通无向图 G 都至少有一个生成树。断开连接的图没有任何生成树，因为它不能生成到其所有顶点。

生成树

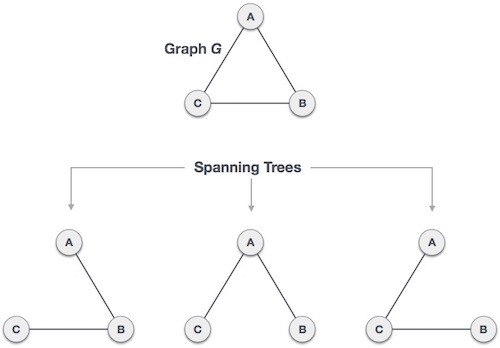
我们在一张完整的图中发现了三棵生成树。完全无向图最多可以有n n-2 个生成树，其中n是节点数。在上述示例中，n 为 3，因此3 3−2 = 3 个生成树是可能的。

生成树的一般性质

我们现在知道一张图可以有多个生成树。以下是连接到图 G 的生成树的一些属性 -

  • 连通图 G 可以有多个生成树。

  • 图 G 的所有可能的生成树都具有相同数量的边和顶点。

  • 生成树没有任何环（循环）。

  • 从生成树中删除一条边将使图断开，即生成树是最小连接的。

  • 向生成树添加一条边将创建一个环路或环路，即生成树最大程度地是非循环的。

生成树的数学性质

  • 生成树有n-1条边，其中n是节点（顶点）的数量。

  • 从完整图中，通过删除最大e - n + 1条边，我们可以构造一棵生成树。

  • 完整图最多可以有n n-2个生成树。

因此，我们可以得出结论，生成树是连通图 G 的子集，而断开图没有生成树。

生成树的应用

生成树主要用于寻找连接图中所有节点的最小路径。生成树的常见应用是 -

  • 民用网络规划

  • 计算机网络路由协议

  • 聚类分析

让我们通过一个小例子来理解这一点。将城市网络视为一个巨大的图，现在计划部署电话线路，以便以最少的线路连接到所有城市节点。这就是生成树出现的地方。

最小生成树 (MST)

在加权图中，最小生成树是比同一图的所有其他生成树具有最小权重的生成树。在现实世界中，该权重可以用距离、拥塞、流量负载或表示边缘的任意值来衡量。

最小生成树算法

我们将在这里学习两种最重要的生成树算法 -

两者都是贪心算法。