
- 数据结构与算法
- DSA - 主页
- DSA - 概述
- DSA - 环境设置
- 数据结构
- DSA - 数据结构基础知识
- DSA - 数据结构和类型
- DSA - 数组数据结构
- 链表
- DSA - 链表基础知识
- DSA - 双向链表
- DSA - 循环链表
- 堆栈和队列
- DSA - 堆栈
- DSA - 表达式解析
- DSA-队列
- 图数据结构
- DSA - 图数据结构
- DSA-深度优先遍历
- DSA-广度优先遍历
- DSA——生成树
- 树数据结构
- DSA - 树数据结构
- DSA - 树遍历
- DSA - 二叉搜索树
- DSA - AVL 树
- DSA - 红黑树
- DSA - B 树
- DSA - B+ 树
- DSA - 八字树
- DSA - 尝试
- DSA-堆
- 递归
- DSA - 递归基础知识
- DSA - 河内塔
- DSA - 斐波那契数列
- DSA 有用资源
- DSA - 问题与解答
- DSA - 快速指南
- DSA - 有用的资源
- DSA - 讨论
数据结构与算法 - 快速指南
数据结构与算法 - 概述
数据结构是一种组织数据以有效使用数据的系统方法。以下术语是数据结构的基础术语。
接口- 每个数据结构都有一个接口。接口表示数据结构支持的操作集。接口仅提供支持的操作列表、它们可以接受的参数类型以及这些操作的返回类型。
实现- 实现提供数据结构的内部表示。实现还提供了数据结构操作中使用的算法的定义。
数据结构的特征
正确性- 数据结构实现应该正确实现其接口。
时间复杂度- 数据结构操作的运行时间或执行时间必须尽可能小。
空间复杂度- 数据结构操作的内存使用量应尽可能少。
对数据结构的需求
随着应用程序变得越来越复杂且数据越来越丰富,应用程序现在面临三个常见问题。
数据搜索- 考虑商店的100 万(10 6 )件商品的库存。如果应用程序要搜索一个项目,则每次都必须在 100 万(10 6 )个项目中搜索一个项目,这会减慢搜索速度。随着数据的增长,搜索会变得更慢。
处理器速度- 虽然处理器速度非常高,但如果数据增长到十亿条记录,处理器速度就会受到限制。
多个请求- 由于数千个用户可以在 Web 服务器上同时搜索数据,因此即使是快速服务器在搜索数据时也会失败。
为了解决上述问题,数据结构来了。数据可以以这样的方式组织在数据结构中:可以不需要搜索所有项目,并且几乎可以立即搜索到所需的数据。
执行时间案例
通常使用三种情况以相对方式比较各种数据结构的执行时间。
最坏情况- 这是特定数据结构操作花费最大时间的情况。如果操作的最坏情况时间为 f(n),则该操作将不会花费超过 f(n) 时间,其中 f(n) 表示 n 的函数。
平均情况- 这是描述数据结构操作的平均执行时间的场景。如果执行一个操作需要 f(n) 时间,则 m 个操作将花费 mf(n) 时间。
最佳情况- 这是描述数据结构操作的最短可能执行时间的场景。如果执行操作需要 f(n) 时间,则实际操作可能需要时间作为随机数,该随机数最大为 f(n)。
基本术语
数据- 数据是值或值集。
数据项- 数据项是指单个值单位。
组项- 分为子项的数据项称为组项。
基本项- 无法分割的数据项称为基本项。
属性和实体- 实体是包含某些可以分配值的属性或属性的实体。
实体集- 具有相似属性的实体形成实体集。
字段- 字段是表示实体属性的单个基本信息单元。
记录- 记录是给定实体的字段值的集合。
文件- 文件是给定实体集中实体记录的集合。
数据结构 - 环境设置
本地环境设置
如果您仍然愿意设置 C 编程语言环境,则您的计算机上需要有以下两个工具:(a) 文本编辑器和 (b) C 编译器。
文本编辑器
这将用于输入您的程序。少数编辑器的示例包括 Windows 记事本、操作系统编辑命令、Brief、Epsilon、EMACS 和 vim 或 vi。
文本编辑器的名称和版本可能因不同操作系统而异。例如,记事本将在 Windows 上使用,vim 或 vi 可以在 Windows 以及 Linux 或 UNIX 上使用。
您使用编辑器创建的文件称为源文件,包含程序源代码。C 程序的源文件通常以扩展名“ .c ”命名。
在开始编程之前,请确保您有一个文本编辑器,并且您有足够的经验来编写计算机程序、将其保存在文件中、编译并最终执行它。
C 编译器
源文件中编写的源代码是程序的人类可读源。它需要被“编译”,变成机器语言,这样你的CPU才能真正按照给定的指令执行程序。
该 C 编程语言编译器将用于将源代码编译为最终的可执行程序。我们假设您具有有关编程语言编译器的基本知识。
最常用且免费的编译器是 GNU C/C++ 编译器。否则,如果您有各自的操作系统 (OS),则可以使用 HP 或 Solaris 的编译器。
以下部分将指导您如何在各种操作系统上安装 GNU C/C++ 编译器。我们一起提及 C/C++ 是因为 GNU GCC 编译器适用于 C 和 C++ 编程语言。
在 UNIX/Linux 上安装
如果您使用的是Linux 或 UNIX,请通过从命令行输入以下命令来检查您的系统上是否安装了 GCC -
$ gcc -v
如果您的计算机上安装了 GNU 编译器,那么它应该打印如下消息 -
Using built-in specs. Target: i386-redhat-linux Configured with: ../configure --prefix = /usr ....... Thread model: posix gcc version 4.1.2 20080704 (Red Hat 4.1.2-46)
如果未安装 GCC,则您必须使用https://gcc.gnu.org/install/上提供的详细说明自行安装它
本教程是基于 Linux 编写的,所有给出的示例都是在 Linux 系统的 Cent OS 版本上编译的。
Mac 操作系统上的安装
如果您使用Mac OS X,获取GCC的最简单方法是从Apple网站下载Xcode开发环境并按照简单的安装说明进行操作。设置 Xcode 后,您将能够使用 C/C++ 的 GNU 编译器。
Xcode 目前可在developer.apple.com/technologies/tools/上获取
在 Windows 上安装
要在Windows上安装GCC,您需要安装MinGW。要安装 MinGW,请访问 MinGW 主页www.mingw.org,然后点击链接进入 MinGW 下载页面。下载最新版本的 MinGW 安装程序,该程序应命名为 MinGW-<version>.exe。
安装 MinWG 时,您至少必须安装 gcc-core、gcc-g++、binutils 和 MinGW 运行时,但您可能希望安装更多。
将 MinGW 安装的 bin 子目录添加到PATH环境变量中,以便您可以在命令行上通过简单名称指定这些工具。
安装完成后,您将能够从 Windows 命令行运行 gcc、g++、ar、ranlib、dlltool 和其他几个 GNU 工具。
数据结构 - 算法基础
算法是一个逐步的过程,它定义了一组按一定顺序执行以获得所需输出的指令。算法通常是独立于底层语言而创建的,即算法可以用多种编程语言来实现。
从数据结构的角度来看,以下是一些重要的算法类别 -
搜索- 搜索数据结构中的项目的算法。
排序- 按特定顺序对项目进行排序的算法。
插入- 在数据结构中插入项目的算法。
更新- 更新数据结构中现有项目的算法。
删除- 从数据结构中删除现有项目的算法。
算法的特点
并不是所有的过程都可以称为算法。算法应具有以下特征 -
明确- 算法应该清晰且明确。它的每个步骤(或阶段)及其输入/输出都应该清晰,并且必须仅产生一个含义。
输入- 算法应该有 0 个或多个明确定义的输入。
输出- 算法应该有 1 个或多个明确定义的输出,并且应该与所需的输出相匹配。
有限性- 算法必须在有限数量的步骤后终止。
可行性- 在可用资源下应该可行。
独立- 算法应该有逐步的方向,它应该独立于任何编程代码。
如何编写算法?
编写算法没有明确的标准。相反,它依赖于问题和资源。算法从来都不是为了支持特定的编程代码而编写的。
我们知道,所有编程语言都共享基本的代码结构,例如循环(do、for、while)、流程控制(if-else)等。这些通用结构可用于编写算法。
我们以一步一步的方式编写算法,但情况并非总是如此。算法编写是一个过程,是在问题域明确之后执行的。也就是说,我们应该了解我们正在设计解决方案的问题领域。
例子
让我们尝试通过一个例子来学习算法编写。
问题- 设计一个算法来添加两个数字并显示结果。
Step 1 − START Step 2 − declare three integers a, b & c Step 3 − define values of a & b Step 4 − add values of a & b Step 5 − store output of step 4 to c Step 6 − print c Step 7 − STOP
算法告诉程序员如何编写程序。或者,该算法可以写为 -
Step 1 − START ADD Step 2 − get values of a & b Step 3 − c ← a + b Step 4 − display c Step 5 − STOP
在算法的设计和分析中,通常采用第二种方法来描述算法。它使分析人员可以轻松分析算法,忽略所有不需要的定义。他可以观察正在使用哪些操作以及流程如何流动。
写步骤号, 是可选的。
我们设计一种算法来解决给定问题。一个问题可以通过多种方式解决。

因此,对于给定问题可以导出许多解决算法。下一步是分析这些提出的解决方案算法并实施最合适的解决方案。
算法分析
算法的效率可以在两个不同的阶段进行分析:实施前和实施后。它们如下 -
先验分析- 这是算法的理论分析。算法的效率是通过假设所有其他因素(例如处理器速度)恒定并且对实现没有影响来衡量的。
事后分析- 这是算法的实证分析。所选算法是使用编程语言实现的。然后在目标计算机上执行此操作。在此分析中,会收集实际的统计信息,例如运行时间和所需空间。
我们将学习先验算法分析。算法分析涉及所涉及的各种操作的执行或运行时间。操作的运行时间可以定义为每个操作执行的计算机指令的数量。
算法复杂度
假设X是一个算法,n是输入数据的大小,算法X使用的时间和空间是决定X效率的两个主要因素。
时间因素- 时间是通过计算关键操作的数量来衡量的,例如排序算法中的比较。
空间因子- 空间是通过计算算法所需的最大内存空间来测量的。
算法的复杂度f(n)给出了算法所需的运行时间和/或存储空间,以n作为输入数据的大小。
空间复杂度
算法的空间复杂度表示算法在其生命周期内所需的内存空间量。算法所需的空间等于以下两个部分的总和 -
固定部分,是存储某些数据和变量所需的空间,与问题的大小无关。例如,使用的简单变量和常量、程序大小等。
变量部分是变量所需的空间,其大小取决于问题的大小。例如动态内存分配、递归栈空间等。
任何算法 P 的空间复杂度 S(P) 为 S(P) = C + SP(I),其中 C 是算法的固定部分,S(I) 是算法的可变部分,这取决于实例特征 I。是一个试图解释这个概念的简单例子 -
Algorithm: SUM(A, B) Step 1 - START Step 2 - C ← A + B + 10 Step 3 - Stop
这里我们有 3 个变量 A、B 和 C 以及 1 个常量。因此 S(P) = 1 + 3。现在,空间取决于给定变量的数据类型和常量类型,并且空间将相应地相乘。
时间复杂度
算法的时间复杂度表示算法运行完成所需的时间量。时间要求可以定义为数值函数 T(n),其中 T(n) 可以用步骤数来衡量,前提是每个步骤消耗恒定的时间。
例如,两个 n 位整数相加需要n步。因此,总计算时间为 T(n) = c * n,其中 c 是两位相加所花费的时间。在这里,我们观察到 T(n) 随着输入大小的增加而线性增长。
数据结构-渐近分析
算法的渐近分析是指定义其运行时性能的数学基础/框架。使用渐近分析,我们可以很好地得出算法的最佳情况、平均情况和最坏情况。
渐近分析是输入限制的,即,如果算法没有输入,则得出结论在恒定时间内工作。除了“输入”之外,所有其他因素都被认为是恒定的。
渐近分析是指以数学计算单位计算任何操作的运行时间。例如,一个操作的运行时间计算为 f(n),而另一操作的运行时间可能计算为g (n 2 )。这意味着第一个操作的运行时间将随着n的增加而线性增加,而第二个操作的运行时间将随着n的增加而呈指数增加。类似地,如果n非常小,则两个操作的运行时间将几乎相同。
通常,算法所需的时间分为三种类型 -
最佳情况- 程序执行所需的最短时间。
平均情况- 程序执行所需的平均时间。
最坏情况- 程序执行所需的最长时间。
渐近符号
以下是计算算法运行时间复杂度的常用渐近符号。
Ο - 大哦符号
Ω - 大欧米茄表示法
θ - Theta 表示法
o - 小哦符号
ω - 小欧米茄符号
大哦符号,Ο
符号 Ο(n) 是表达算法运行时间上限的正式方式。它测量最坏情况的时间复杂度或算法完成可能需要的最长时间。

例如,对于函数f (n)
Ο(f(n)) = { g(n) : there exists c > 0 and n0 such that g(n) ≤ c.f(n) for all n > n0. }
例子
让我们考虑一个给定的函数,f ( n ) = 4. n 3 +10。n 2 + 5。n +1。
考虑g(n) = n 3
f ( n ) ≥ 5。g ( n )对于所有n > 2 的值。
因此, f ( n )的复杂度可以表示为O ( g ( n )),即O ( n 3 )。
大欧米茄表示法,Ω
符号 Ω(n) 是表达算法运行时间下限的正式方式。它衡量最佳情况的时间复杂度或算法完成可能需要的最佳时间。

例如,对于函数f ( n )
Ω(f(n)) ≥ { g(n) : there exists c > 0 and n0 such that g(n) ≤ c.f(n) for all n > n0. }
例子
让我们考虑一个给定的函数,f ( n ) = 4. n 3 +10。n 2 + 5。n +1
考虑到g ( n ) = n 3,f ( n ) ≥ 4。对于所有n > 0 的值,g ( n )。
因此, f ( n )的复杂度可以表示为Ω ( g ( n )),即Ω ( n 3 )。
Theta 表示法,θ
符号 θ(n) 是表达算法运行时间的下限和上限的正式方式。有些人可能会将 theta 表示法与平均情况时间复杂度混淆;虽然大θ符号几乎可以准确地用于描述平均情况,但也可以使用其他符号。它表示如下 -

θ(f(n)) = { g(n) if and only if g(n) = Ο(f(n)) and g(n) = Ω(f(n)) for all n > n0. }
例子
让我们考虑一个给定的函数,f ( n ) = 4. n 3 +10。n 2 + 5。n +1
考虑g ( n ) = n 3 , 4. g ( n )≤ f ( n ) ≤ 5.对于n 的所有值,g ( n )。
因此, f ( n )的复杂度可以表示为Ɵ ( g ( n )),即Ɵ ( n 3 )。
小 Oh (o) 和小 Omega (ω) 符号
Little Oh 和 Little Omega 表示法也代表了最好和最坏情况的复杂性,但与 Big Oh 和 Big Omega 表示法相比,它们并不是渐近紧的。因此,最常用的表示时间复杂度的符号只有 Big Oh 和 Big Omega 符号。
常见渐近符号
以下是一些常见渐近符号的列表 -
| 持续的 | - | 复杂度(1) |
| 对数 | - | O(logn) |
| 线性 | - | 在) |
| 对数 n | - | O(n log n) |
| 二次的 | - | O(n 2 ) |
| 立方体 | - | O(n 3 ) |
| 多项式 | - | nO (1) |
| 指数 | - | 2 O(n) |
数据结构 - 贪心算法
算法旨在实现给定问题的最佳解决方案。在贪婪算法方法中,决策是根据给定的解决方案域做出的。由于贪婪,因此选择似乎提供最佳解决方案的最接近的解决方案。
贪心算法试图找到局部最优解,这最终可能导致全局优化解。然而,一般贪心算法不提供全局优化的解决方案。
数硬币
这个问题是通过选择尽可能少的硬币来计数到所需的值,而贪心方法迫使算法选择尽可能大的硬币。如果我们提供了 1、2、5 和 10 欧元的硬币,并且要求我们数 18 欧元,那么贪心程序将是 -
1 - 选择一枚 10 欧元硬币,剩余数量为 8
2 - 然后选择一枚 5 欧元硬币,剩余数量为 3
3 - 然后选择一枚 2 欧元硬币,剩余数量为 1
4 - 最后,选择一枚 1 欧元硬币解决了问题
不过,它似乎运行良好,对于这个计数,我们只需要挑选 4 个硬币。但如果我们稍微改变一下问题,那么同样的方法可能无法产生同样的最佳结果。
对于货币系统,我们有 1、7、10 面值的硬币,计算 18 面值的硬币绝对是最佳选择,但对于 15 面值的硬币,可能会使用比所需更多的硬币。例如,贪婪方法将使用 10 + 1 + 1 + 1 + 1 + 1,总共 6 个硬币。而同样的问题只需使用 3 个硬币即可解决(7 + 7 + 1)
因此,我们可以得出结论,贪婪方法会选择立即优化的解决方案,并且在全局优化是主要问题的情况下可能会失败。
例子
大多数网络算法都使用贪婪方法。这是其中一些的列表 -
旅行商问题
Prim 的最小生成树算法
Kruskal 的最小生成树算法
Dijkstra 的最小生成树算法
图表 - 地图着色
图 - 顶点覆盖
背包问题
作业调度问题
有很多类似的问题都使用贪心方法来寻找最优解。
数据结构 - 分而治之
为了理解算法的分而治之的设计策略,让我们使用一个简单的现实例子。考虑一个例子,我们需要梳理 C 型卷发并去除其中的所有结。为此,第一步是将头发分成较小的发丝,这样比梳理头发更容易梳理。同样的技术也适用于算法。
分治法将一个问题递归地分解为多个子问题,直到无法进一步划分为止。首先解决这些子问题,然后将解决方案合并在一起形成最终解决方案。
分而治之设计技术的常见程序如下 -
划分- 我们将原始问题划分为多个子问题,直到它们无法进一步划分。
征服- 然后借助递归分别解决这些子问题
合并- 一旦解决,所有子问题都会合并/组合在一起,形成原始问题的最终解决方案。
有多种方法可以为分而治之的算法设计模式提供输入。使用的两种主要数据结构是 -数组和链表。它们的用法解释为
数组作为输入
各种算法可以采用多种方式获取输入,以便可以使用分而治之技术来解决它们。数组就是其中之一。在需要输入为列表形式的算法中,如各种排序算法,最常用的是数组数据结构。
在下面的排序算法的输入中,数组输入被划分为子问题,直到它们无法进一步划分为止。

然后,对子问题进行排序(征服步骤)并合并以形成原始数组的解决方案(组合步骤)。

由于数组是索引和线性数据结构,因此排序算法最普遍使用数组数据结构来接收输入。
链表作为输入
另一种可用于为分而治之算法获取输入的数据结构是链表(例如,使用链表的合并排序)。与数组一样,链表也是顺序存储数据的线性数据结构。
考虑链表上的归并排序算法;按照非常流行的龟兔赛跑算法,对列表进行划分,直到不能再划分为止。

然后,对列表中的节点进行排序(征服)。然后递归地组合(或合并)这些节点,直到获得最终解决方案。

由于链表不是索引的线性数据结构,因此还可以使用稍微不同的技术对链表数据结构执行各种搜索算法。必须使用列表节点中可用的指针来处理它们。
例子
以下计算机算法基于分而治之的编程方法 -
归并排序
快速排序
二分查找
施特拉森矩阵乘法
最近的一对
解决任何计算机问题都有多种方法,但提到的方法是分而治之的一个很好的例子。
数据结构 - 动态规划
动态规划方法类似于分而治之,将问题分解为更小的可能的子问题。但与分而治之不同的是,这些子问题不是独立解决的。相反,这些较小的子问题的结果被记住并用于类似或重叠的子问题。
动态规划用于我们遇到问题的地方,可以将问题分成相似的子问题,以便可以重复使用它们的结果。大多数情况下,这些算法用于优化。在解决当前的子问题之前,动态算法将尝试检查先前解决的子问题的结果。将子问题的解组合起来,以获得最佳解。
所以我们可以说 -
问题应该能够分为更小的重叠子问题。
可以通过使用较小子问题的最优解来获得最优解。
动态算法使用记忆化。

比较
与解决局部优化的贪婪算法相反,动态算法的动机是对问题进行整体优化。
与分治算法不同,动态算法使用较小子问题的输出,然后尝试优化较大的子问题。动态算法使用记忆化来记住已解决的子问题的输出。
例子
以下计算机问题可以使用动态规划方法来解决 -
- 斐波那契数列
- 背包问题
- 河内塔
- Floyd-Warshall 的所有对最短路径
- Dijkstra 的最短路径
- 项目调度
动态规划既可以采用自上而下的方式,也可以采用自下而上的方式。当然,大多数时候,就 CPU 周期而言,参考先前的解决方案输出比重新计算更便宜。
数据结构与算法基本概念
本章解释与数据结构相关的基本术语。
数据定义
数据定义定义了具有以下特征的特定数据。
Atomics- 定义应该定义一个单一的概念。
可追踪- 定义应该能够映射到某些数据元素。
准确- 定义应该明确。
清晰简洁- 定义应该是可以理解的。
数据对象
数据对象表示具有数据的对象。
数据类型
数据类型是对整数、字符串等各种类型的数据进行分类的一种方式,它决定了相应类型的数据可以使用的值、可以对相应类型的数据执行的操作类型。有两种数据类型 -
- 内置数据类型
- 派生数据类型
内置数据类型
语言内置支持的那些数据类型称为内置数据类型。例如,大多数语言都提供以下内置数据类型。
- 整数
- 布尔值(真、假)
- 浮点数(十进制数)
- 字符和字符串
派生数据类型
那些独立于实现的数据类型,因为它们可以以一种或另一种方式实现,被称为派生数据类型。这些数据类型通常是通过主数据类型或内置数据类型及其关联操作的组合来构建的。例如 -
- 列表
- 大批
- 堆
- 队列
基本操作
数据结构中的数据通过一定的操作进行处理。所选择的特定数据结构很大程度上取决于需要对该数据结构执行的操作的频率。
- 穿越
- 搜寻中
- 插入
- 删除
- 排序
- 合并
数据结构和类型
引入数据结构是为了用编程语言存储、组织和操作数据。它们的设计方式使数据的访问和处理变得更加容易和简单。这些数据结构并不局限于一种特定的编程语言;它们只是在内存中构建数据的代码片段。
数据类型经常被混淆为一种数据结构类型,但即使它们被称为抽象数据类型,它也不完全正确。数据类型代表数据的性质,而数据结构只是相似或不同数据类型的集合。
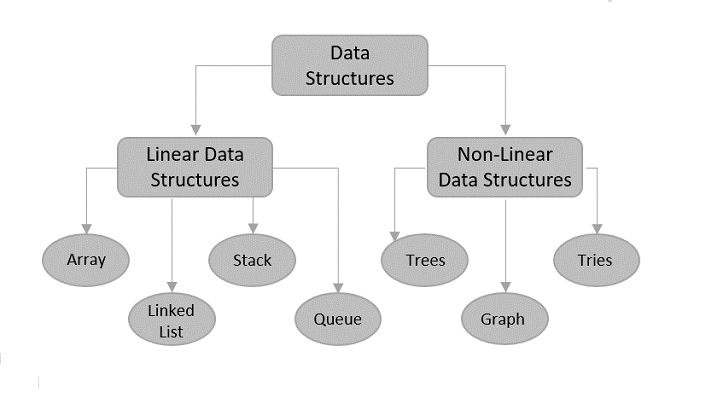
通常只有两种类型的数据结构 -
线性
非线性
线性数据结构
数据按顺序存储在线性数据结构中。这些是基本结构,因为元素是一个接一个地存储的,而不应用任何数学运算。

线性数据结构通常很容易实现,但由于内存分配可能变得复杂,时间和空间复杂度增加。线性数据结构的几个例子包括 -
数组
链表
堆栈
队列
根据数据存储方法,这些线性数据结构分为两个子类型。它们是 -静态和动态数据结构。
静态线性数据结构
在静态线性数据结构中,内存分配是不可扩展的。一旦使用了整个内存,就无法再检索空间来存储更多数据。因此,需要根据程序的大小来预留内存。这也将成为一个缺点,因为保留比所需更多的内存可能会导致内存块的浪费。
静态线性数据结构的最佳示例是数组。
动态线性数据结构
在动态线性数据结构中,可以在需要时动态地进行内存分配。考虑到程序的空间复杂度,这些数据结构是有效的。
动态线性数据结构的例子包括:链表、堆栈和队列。
非线性数据结构
非线性数据结构以层次结构的形式存储数据。因此,与线性数据结构相比,数据可以在多个层次上找到并且难以遍历。
然而,它们旨在克服线性数据结构的问题和限制。例如,线性数据结构的主要缺点是内存分配。由于数据在线性数据结构中按顺序分配,因此这些数据结构中的每个元素都使用一整个内存块。但是,如果数据使用的内存少于分配的块可以容纳的内存,则块中的额外内存空间就会被浪费。因此,引入了非线性数据结构。它们降低了空间复杂度并优化使用内存。
非线性数据结构的几种类型是 -
图表
树木
尝试
地图
数据结构和算法 - 数组
数组是一种线性数据结构,被定义为具有相同或不同数据类型的元素的集合。它们既存在于单维度又存在于多维度。当需要将多个性质相似的元素存储在一个地方时,这些数据结构就会出现。

数组索引和内存地址之间的区别在于,数组索引就像一个键值来标记数组中的元素。然而,内存地址是可用空闲内存的起始地址。
以下是理解数组概念的重要术语。
元素- 存储在数组中的每个项目称为元素。
索引- 数组中元素的每个位置都有一个数字索引,用于标识该元素。
句法
用C和C++编程语言创建数组-
data_type array_name[array_size] = {elements separated using commas}
or,
data_type array_name[array_size];
用JAVA编程语言创建数组-
data_type[] array_name = {elements separated by commas}
or,
data_type array_name = new data_type[array_size];
需要数组
数组可用作许多问题的解决方案,从小型排序问题到更复杂的问题(例如旅行推销员问题)。除了数组之外,还有许多数据结构可以为这些问题提供高效的时间和空间复杂度,那么什么使使用数组更好呢?答案在于随机访问查找时间。
数组提供O(1)随机访问查找时间。这意味着,访问数组的第 1个索引和访问数组的第 1000个索引将花费相同的时间。这是因为数组带有一个指针和一个偏移值。指针指向内存的正确位置,偏移值显示在所述内存中查找多远。
array_name[index]
| |
Pointer Offset
因此,在具有 6 个元素的数组中,要访问第 1 个元素,数组将指向第 0 个索引。类似地,要访问第 6个元素,数组将指向第 5个索引。
数组表示
数组表示为桶的集合,其中每个桶存储一个元素。这些存储桶的索引范围为“0”到“n-1”,其中 n 是该特定数组的大小。例如,大小为 10 的数组将具有索引从 0 到 9 的存储桶。
对于多维数组,该索引也类似。如果是二维数组,每个桶中都会有子桶。然后它将被索引为 array_name[m][n],其中 m 和 n 是数组中每个级别的大小。

根据上图,以下是需要考虑的要点。
索引从0开始。
数组长度为9,这意味着它可以存储9个元素。
每个元素都可以通过其索引来访问。例如,我们可以将索引 6 处的元素获取为 23。
数组中的基本操作
数组的基本操作是插入、删除、查找、显示、遍历和更新。执行这些操作通常是为了修改阵列中的数据或报告阵列的状态。
以下是数组支持的基本操作。
遍历- 逐一打印所有数组元素。
插入- 在给定索引处添加一个元素。
删除- 删除给定索引处的元素。
搜索- 使用给定索引或值搜索元素。
更新- 更新给定索引处的元素。
显示- 显示数组的内容。
在 C 中,当使用大小初始化数组时,它会按以下顺序为其元素分配默认值。
| 数据类型 | 默认值 |
|---|---|
| 布尔值 | 错误的 |
| 字符 | 0 |
| 整数 | 0 |
| 漂浮 | 0.0 |
| 双倍的 | 0.0f |
| 空白 | |
| wchar_t | 0 |
插入操作
在插入操作中,我们向数组添加一个或多个元素。根据需要,可以在数组的开头、结尾或任何给定索引处添加新元素。这是使用编程语言的输入语句来完成的。
算法
以下是将元素插入线性数组直到到达数组末尾的算法 -
1. Start 2. Create an Array of a desired datatype and size. 3. Initialize a variable ‘i’ as 0. 4. Enter the element at ith index of the array. 5. Increment i by 1. 6. Repeat Steps 4 & 5 until the end of the array. 7. Stop
在这里,我们看到了插入操作的实际实现,我们在数组末尾添加数据 -
例子
#include <stdio.h>
int main(){
int LA[3], i;
printf("Array Before Insertion:\n");
for(i = 0; i < 3; i++)
printf("LA[%d] = %d \n", i, LA[i]);
printf("Inserting Elements.. ");
printf("The array elements after insertion :\n"); // prints array values
for(i = 0; i < 3; i++) {
LA[i] = i + 2;
printf("LA[%d] = %d \n", i, LA[i]);
}
return 0;
}
输出
Array Before Insertion: LA[0] = 587297216 LA[1] = 32767 LA[2] = 0 Inserting Elements.. The array elements after insertion : LA[0] = 2 LA[1] = 3 LA[2] = 4
#include <iostream>
using namespace std;
int main(){
int LA[3], i;
cout << "Array Before Insertion:" << endl;
for(i = 0; i < 3; i++)
cout << "LA[" << i <<"] = " << LA[i] << endl;
//prints garbage values
cout << "Inserting elements.." <<endl;
cout << "Array After Insertion:" << endl; // prints array values
for(i = 0; i < 5; i++) {
LA[i] = i + 2;
cout << "LA[" << i <<"] = " << LA[i] << endl;
}
return 0;
}
输出
Array Before Insertion: LA[0] = -1834117968 LA[1] = 32767LA[2] = 0 Inserting elements.. Array After Insertion: LA[0] = 2 LA[1] = 3 LA[2] = 4 LA[5] = 0
public class ArrayDemo {
public static void main(String []args) {
int LA[] = new int[3];
System.out.println("Array Before Insertion:");
for(int i = 0; i < 3; i++)
System.out.println("LA[" + i + "] = " + LA[i]); //prints empty array
System.out.println("Inserting Elements..");
// Printing Array after Insertion
System.out.println("Array After Insertion:");
for(int i = 0; i < 3; i++) {
LA[i] = i+3;
System.out.println("LA[" + i + "] = " + LA[i]);
}
}
}
输出
Array Before Insertion:LA[0] = 0 LA[1] = 0 LA[2] = 0 Inserting Elements.. Array After Insertion: LA[0] = 3 LA[1] = 4 LA[2] = 5
有关数组插入操作的其他变体,请单击此处。
删除操作
在此数组操作中,我们从数组的特定索引中删除一个元素。当我们将后续索引中的值分配给当前索引时,就会发生此删除操作。
算法
考虑 LA 是一个具有 N 个元素的线性数组,K 是一个正整数,使得 K<=N。以下是删除LA第 K个位置上可用元素的算法。
1. Start 2. Set J = K 3. Repeat steps 4 and 5 while J < N 4. Set LA[J] = LA[J + 1] 5. Set J = J+1 6. Set N = N-1 7. Stop
例子
以下是此操作在各种编程语言中的实现 -
#include <stdio.h>
void main(){
int LA[] = {1,3,5};
int n = 3;
int i;
printf("The original array elements are :\n");
for(i = 0; i<n; i++)
printf("LA[%d] = %d \n", i, LA[i]);
for(i = 1; i<n; i++) {
LA[i] = LA[i+1];
n = n – 1;
}
printf("The array elements after deletion :\n");
for(i = 0; i<n-1; i++)
printf("LA[%d] = %d \n", i, LA[i]);
}
输出
The original array elements are : LA[0] = 1 LA[1] = 3 LA[2] = 5 The array elements after deletion : LA[0] = 1 LA[1] = 5
#include <iostream>
using namespace std;
int main(){
int LA[] = {1,3,5};
int i, n = 3;
cout << "The original array elements are :"<<endl;
for(i = 0; i<n; i++) {
cout << "LA[" << i << "] = " << LA[i] << endl;
}
for(i = 1; i<n; i++) {
LA[i] = LA[i+1];
n = n - 1;
}
cout << "The array elements after deletion :"<<endl;
for(i = 0; i<n; i++) {
cout << "LA[" << i << "] = " << LA[i] <<endl;
}
}
输出
The original array elements are : LA[0] = 1 LA[1] = 3 LA[2] = 5 The array elements after deletion : LA[0] = 1 LA[1] = 5
public class ArrayDemo {
public static void main(String []args) {
int LA[] = new int[3];
int n = LA.length;
System.out.println("Array Before Deletion:");
for(int i = 0; i < n; i++) {
LA[i] = i + 3;
System.out.println("LA[" + i + "] = " + LA[i]);
}
for(int i = 1; i<n-1; i++) {
LA[i] = LA[i+1];
n = n - 1;
}
System.out.println("Array After Deletion:");
for(int i = 0; i < n; i++) {
System.out.println("LA[" + i + "] = " + LA[i]);
}
}
}
输出
Array Before Deletion: LA[0] = 3 LA[1] = 4 LA[2] = 5 Array After Deletion: LA[0] = 3 LA[1] = 5
搜索操作
使用键搜索数组中的元素;键元素顺序比较数组中的每个值,以检查该键是否存在于数组中。
算法
考虑 LA 是一个具有 N 个元素的线性数组,K 是一个正整数,使得 K<=N。以下是使用顺序搜索查找值为 ITEM 的元素的算法。
1. Start 2. Set J = 0 3. Repeat steps 4 and 5 while J < N 4. IF LA[J] is equal ITEM THEN GOTO STEP 6 5. Set J = J +1 6. PRINT J, ITEM 7. Stop
例子
以下是此操作在各种编程语言中的实现 -
#include <stdio.h>
void main(){
int LA[] = {1,3,5,7,8};
int item = 5, n = 5;
int i = 0, j = 0;
printf("The original array elements are :\n");
for(i = 0; i<n; i++) {
printf("LA[%d] = %d \n", i, LA[i]);
}
for(i = 0; i<n; i++) {
if( LA[i] == item ) {
printf("Found element %d at position %d\n", item, i+1);
}
}
}
输出
The original array elements are : LA[0] = 1 LA[1] = 3 LA[2] = 5 LA[3] = 7 LA[4] = 8 Found element 5 at position 3
#include <iostream>
using namespace std;
int main(){
int LA[] = {1,3,5,7,8};
int item = 5, n = 5;
int i = 0;
cout << "The original array elements are : " <<endl;
for(i = 0; i<n; i++) {
cout << "LA[" << i << "] = " << LA[i] << endl;
}
for(i = 0; i<n; i++) {
if( LA[i] == item ) {
cout << "Found element " << item << " at position " << i+1 <<endl;
}
}
return 0;
}
输出
The original array elements are : LA[0] = 1 LA[1] = 3 LA[2] = 5 LA[3] = 7 LA[4] = 8 Found element 5 at position 3
public class ArrayDemo{
public static void main(String []args){
int LA[] = new int[5];
System.out.println("Array:");
for(int i = 0; i < 5; i++) {
LA[i] = i + 3;
System.out.println("LA[" + i + "] = " + LA[i]);
}
for(int i = 0; i < 5; i++) {
if(LA[i] == 6)
System.out.println("Element " + 6 + " is found at index " + i);
}
}
}
输出
Array: LA[0] = 3 LA[1] = 4 LA[2] = 5 LA[3] = 6 LA[4] = 7 Element 6 is found at index 3
遍历操作
该操作遍历数组的所有元素。我们使用循环语句来执行此操作。
算法
以下是遍历线性数组中所有元素的算法 -
1 Start 2. Initialize an Array of certain size and datatype. 3. Initialize another variable ‘i’ with 0. 4. Print the ith value in the array and increment i. 5. Repeat Step 4 until the end of the array is reached. 6. End
例子
以下是此操作在各种编程语言中的实现 -
#include <stdio.h>
int main(){
int LA[] = {1,3,5,7,8};
int item = 10, k = 3, n = 5;
int i = 0, j = n;
printf("The original array elements are :\n");
for(i = 0; i<n; i++) {
printf("LA[%d] = %d \n", i, LA[i]);
}
}
输出
The original array elements are : LA[0] = 1 LA[1] = 3 LA[2] = 5 LA[3] = 7 LA[4] = 8
#include <iostream>
using namespace std;
int main(){
int LA[] = {1,3,5,7,8};
int item = 10, k = 3, n = 5;
int i = 0, j = n;
cout << "The original array elements are:\n";
for(i = 0; i<n; i++)
cout << "LA[" << i << "] = " << LA[i] << endl;
return 0;
}
输出
The original array elements are: LA[0] = 1 LA[1] = 3 LA[2] = 5 LA[3] = 7 LA[4] = 8
public class ArrayDemo {
public static void main(String []args) {
int LA[] = new int[5];
System.out.println("The array elements are: ");
for(int i = 0; i < 5; i++) {
LA[i] = i + 2;
System.out.println("LA[" + i + "] = " + LA[i]);
}
}
}
输出
The array elements are: LA[0] = 2 LA[1] = 3 LA[2] = 4 LA[3] = 5 LA[4] = 6
更新操作
更新操作是指更新数组中给定索引处的现有元素。
算法
考虑 LA 是一个具有 N 个元素的线性数组,K 是一个正整数,使得 K<=N。以下是更新 LA 第 K 个位置处可用元素的算法。
1. Start 2. Set LA[K-1] = ITEM 3. Stop
例子
以下是此操作在各种编程语言中的实现 -
#include <stdio.h>
void main(){
int LA[] = {1,3,5,7,8};
int k = 3, n = 5, item = 10;
int i, j;
printf("The original array elements are :\n");
for(i = 0; i<n; i++) {
printf("LA[%d] = %d \n", i, LA[i]);
}
LA[k-1] = item;
printf("The array elements after updation :\n");
for(i = 0; i<n; i++) {
printf("LA[%d] = %d \n", i, LA[i]);
}
}
输出
The original array elements are : LA[0] = 1 LA[1] = 3 LA[2] = 5 LA[3] = 7 LA[4] = 8 The array elements after updation : LA[0] = 1 LA[1] = 3 LA[2] = 10 LA[3] = 7 LA[4] = 8
#include <iostream>
using namespace std;
int main(){
int LA[] = {1,3,5,7,8};
int item = 10, k = 3, n = 5;
int i = 0, j = n;
cout << "The original array elements are :\n";
for(i = 0; i<n; i++)
cout << "LA[" << i << "] = " << LA[i] << endl;
LA[2] = item;
cout << "The array elements after updation are :\n";
for(i = 0; i<n; i++)
cout << "LA[" << i << "] = " << LA[i] << endl;
return 0;
}
输出
The original array elements are : LA[0] = 1 LA[1] = 3 LA[2] = 5 LA[3] = 7 LA[4] = 8 The array elements after updation are : LA[0] = 1 LA[1] = 3 LA[2] = 10 LA[3] = 7 LA[4] = 8
public class ArrayDemo {
public static void main(String []args) {
int LA[] = new int[5];
int item = 15;
System.out.println("The array elements are: ");
for(int i = 0; i < 5; i++) {
LA[i] = i + 2;
System.out.println("LA[" + i + "] = " + LA[i]);
}
LA[3] = item;
System.out.println("The array elements after updation are: ");
for(int i = 0; i < 5; i++)
System.out.println("LA[" + i + "] = " + LA[i]);
}
}
输出
The array elements are: LA[0] = 2 LA[1] = 3 LA[2] = 4 LA[3] = 5 LA[4] = 6 The array elements after updation are: LA[0] = 2 LA[1] = 3 LA[2] = 4 LA[3] = 15 LA[4] = 6
显示操作
此操作使用 print 语句显示整个数组中的所有元素。
算法
1. Start 2. Print all the elements in the Array 3. Stop
例子
以下是此操作在各种编程语言中的实现 -
#include <stdio.h>
int main(){
int LA[] = {1,3,5,7,8};
int n = 5;
int i;
printf("The original array elements are :\n");
for(i = 0; i<n; i++) {
printf("LA[%d] = %d \n", i, LA[i]);
}
}
输出
The original array elements are : LA[0] = 1 LA[1] = 3 LA[2] = 5 LA[3] = 7 LA[4] = 8
#include <iostream>
using namespace std;
int main(){
int LA[] = {1,3,5,7,8};
int n = 5;
int i;
cout << "The original array elements are :\n";
for(i = 0; i<n; i++)
cout << "LA[" << i << "] = " << LA[i] << endl;
return 0;
}
输出
The original array elements are : LA[0] = 1 LA[1] = 3 LA[2] = 5 LA[3] = 7 LA[4] = 8
public class ArrayDemo {
public static void main(String []args) {
int LA[] = new int[5];
System.out.println("The array elements are: ");
for(int i = 0; i < 5; i++) {
LA[i] = i + 2;
System.out.println("LA[" + i + "] = " + LA[i]);
}
}
}
输出
The array elements are: LA[0] = 2 LA[1] = 3 LA[2] = 4 LA[3] = 5 LA[4] = 6
数据结构和算法 - 链表
如果数组容纳相似类型的数据类型,则链表由具有不同数据类型的元素组成,这些元素也按顺序排列。
但这些链表是如何创建的呢?
链表是通过链接连接在一起的“节点”的集合。这些节点由要存储的数据和指向链表中下一个节点的地址的指针组成。对于数组,大小受定义限制,但在链表中,没有定义的大小。任意数量的数据都可以存储在其中,也可以从中删除。
链表分为三种类型 -
单链表- 节点仅指向列表中下一个节点的地址。
双向链表- 节点指向前一个和下一个节点的地址。
循环链表- 列表中的最后一个节点将指向列表中的第一个节点。它可以是单链的,也可以是双链的。
链表表示
链表可以看作是节点链,其中每个节点都指向下一个节点。

根据上图,以下是需要考虑的要点。
链表包含一个称为第一个(头)的链接元素。
每个链接都带有一个数据字段和一个称为 next 的链接字段。
每个链接都使用其下一个链接与其下一个链接链接。
最后一个链接带有一个空链接来标记列表的结尾。
链表的类型
以下是各种类型的链表。
单链表
单链表在一个节点中包含两个“桶”;一个桶保存数据,另一个桶保存列表的下一个节点的地址。遍历只能在一个方向上完成,因为同一列表的两个节点之间只有一条链接。

双向链表
双向链表在一个节点中包含三个“桶”;一个桶保存数据,其他桶保存列表中前一个和下一个节点的地址。由于列表中的节点从两侧相互连接,因此列表被遍历两次。

循环链表
循环链表可以存在于单链表和双向链表中。
由于循环链表的最后一个节点和第一个节点是相连的,所以这个链表中的遍历会一直进行下去,直到被破坏。

链表中的基本操作
链表中的基本操作是插入、删除、搜索、显示和删除给定键处的元素。这些操作在单链表上执行,如下所示 -
插入- 在列表的开头添加一个元素。
删除- 删除列表开头的元素。
显示- 显示完整列表。
搜索- 使用给定键搜索元素。
删除- 使用给定键删除元素。
插入操作
在链表中添加新节点是一项多步骤的活动。我们将在这里通过图表来了解这一点。首先,使用相同的结构创建一个节点并找到它必须插入的位置。

假设我们在中间插入一个节点 B (NewNode)