
- 数字图像处理
- DIP - 主页
- DIP - 图像处理简介
- DIP - 信号与系统介绍
- DIP - 摄影史
- DIP - 应用和使用
- DIP - 尺寸概念
- DIP - 相机上的图像形成
- DIP - 摄像头机构
- DIP - 像素的概念
- DIP-- 透视变换
- DIP - 每像素位数的概念
- DIP - 图像类型
- DIP - 颜色代码转换
- DIP - 灰度到 RGB 转换
- DIP - 抽样的概念
- DIP - 像素分辨率
- DIP - 缩放的概念
- DIP - 缩放方法
- DIP - 空间分辨率
- DIP - 每英寸的像素点和线数
- DIP - 灰度分辨率
- DIP - 量化的概念
- DIP - ISO 偏好曲线
- DIP - 抖动的概念
- DIP - 直方图介绍
- DIP - 亮度和对比度
- DIP - 图像转换
- DIP - 直方图滑动
- DIP - 直方图拉伸
- DIP - 概率导论
- DIP - 直方图均衡
- DIP - 灰度级变换
- DIP - 卷积的概念
- DIP - 掩模的概念
- DIP - 模糊的概念
- DIP - 边缘检测的概念
- DIP - Prewitt 操作员
- DIP - 索贝尔算子
- DIP - 罗宾逊指南针面罩
- DIP - Krisch 指南针掩模
- DIP - 拉普拉斯算子
- DIP - 频域分析
- DIP - 傅里叶级数和变换
- DIP——卷积定理
- DIP - 高通滤波器与低通滤波器
- DIP - 色彩空间简介
- DIP - JPEG 压缩
- DIP - 光学字符识别
- DIP - 计算机视觉和图形
- DIP 有用资源
- DIP - 快速指南
- DIP - 有用的资源
- DIP - 讨论
DIP - 快速指南
数字图像处理简介
介绍
信号处理是电气工程和数学中的一门学科,涉及模拟和数字信号的分析和处理,以及信号的存储、过滤和其他操作。这些信号包括传输信号、声音或语音信号、图像信号以及其他信号等。
在所有这些信号中,处理输入是图像且输出也是图像的信号类型的领域是在图像处理中完成的。顾名思义,它涉及图像处理。
它又可以分为模拟图像处理和数字图像处理。
模拟图像处理
模拟图像处理是对模拟信号进行的。它包括对二维模拟信号的处理。在这种类型的处理中,通过改变电信号通过电手段来操纵图像。常见的例子包括电视图像。
随着时间的推移,数字图像处理由于其更广泛的应用范围而逐渐取代了模拟图像处理。
数字图像处理
数字图像处理涉及开发对数字图像执行操作的数字系统。
什么是图像
图像只不过是二维信号。它由数学函数 f(x,y) 定义,其中 x 和 y 是水平和垂直的两个坐标。
任意点的 f(x,y) 值给出了图像该点的像素值。

上图是您现在在计算机屏幕上查看的数字图像的示例。但实际上,该图像只不过是一个范围在 0 到 255 之间的数字的二维数组。
| 128 | 30 | 123 |
| 第232章 | 123 | 321 |
| 123 | 77 | 89 |
| 80 | 255 | 255 |
每个数字代表函数 f(x,y) 在任意点的值。在这种情况下,值128、230,123各自表示单独的像素值。图片的维度实际上就是这个二维数组的维度。
数字图像和信号之间的关系
如果图像是二维数组,那么它与信号有什么关系?为了理解这一点,我们首先需要了解什么是信号?
信号
在物理世界中,任何可通过时间、空间或任何更高维度测量的量都可以视为信号。信号是一个数学函数,它传达一些信息。信号可以是一维或二维或更高维的信号。一维信号是随时间测量的信号。常见的例子是语音信号。二维信号是通过一些其他物理量测量的信号。二维信号的例子是数字图像。我们将在下一个教程中更详细地了解如何形成和解释一维或二维信号以及更高的信号。
关系
因为在物理世界中两个观察者之间传递信息或广播消息的任何东西都是信号。这包括作为信号的语音或(人声)或图像。因为当我们说话时,我们的声音会转换为声波/信号,并根据与我们交谈的人的时间进行转换。不仅如此,还有数码相机的工作方式,因为从数码相机获取图像涉及将信号从系统的一个部分传输到另一部分。
数字图像是如何形成的
由于从相机捕获图像是一个物理过程。阳光被用作能源。传感器阵列用于采集图像。因此,当阳光照射到物体上时,传感器会感测到该物体反射的光量,并根据感测到的数据量生成连续的电压信号。为了创建数字图像,我们需要将这些数据转换为数字形式。这涉及到采样和量化。(稍后讨论)。采样和量化的结果产生二维数组或数字矩阵,它们只不过是数字图像。
重叠字段
机器/计算机视觉
机器视觉或计算机视觉涉及开发一个系统,其中输入是图像,输出是一些信息。例如:开发一个扫描人脸并打开任何类型的锁的系统。这个系统看起来像这样。

电脑图像
计算机图形学处理从对象模型形成图像,而不是通过某些设备捕获图像。例如:对象渲染。从对象模型生成图像。这样的系统看起来像这样。

人工智能
人工智能或多或少是一门将人类智能融入机器的研究。人工智能在图像处理方面有很多应用。例如:开发计算机辅助诊断系统,帮助医生解释X射线、MRI等图像,然后突出显示医生要检查的显着部分。
信号处理
信号处理是一个保护伞,图像处理位于它的下面。物理世界(3D 世界)中的物体反射的光量通过相机的镜头,变成 2D 信号,从而形成图像。然后使用信号处理方法对该图像进行数字化,然后在数字图像处理中对该数字图像进行操作。
信号与系统简介
本教程涵盖了理解数字图像处理概念所需的信号和系统基础知识。在讨论详细概念之前,我们首先定义简单的术语。
信号
在电气工程中,表示某些信息的基本量称为信号。信息是什么并不重要,即:模拟信息或数字信息。在数学中,信号是传递某些信息的函数。事实上,任何可通过时间、空间或任何更高维度测量的量都可以视为信号。信号可以是任何维度并且可以是任何形式。
模拟信号
信号可以是模拟量,这意味着它是根据时间定义的。它是一个连续信号。这些信号是通过连续自变量定义的。它们很难分析,因为它们带有大量的值。由于值样本很大,它们非常准确。为了存储这些信号,您需要无限的内存,因为它可以在实线上实现无限的值。模拟信号用正弦波表示。
例如:
人声
人声是模拟信号的一个例子。当你说话时,产生的声音以压力波的形式在空气中传播,因此属于一个数学函数,具有空间和时间的独立变量以及与气压相对应的值。
另一个例子是正弦波,如下图所示。
Y = sin(x) 其中 x 是独立的

数字信号
与模拟信号相比,数字信号非常容易分析。它们是不连续的信号。它们是模拟信号的挪用。
数字一词代表离散值,因此意味着它们使用特定值来表示任何信息。在数字信号中,仅使用两个值来表示某些内容,即:1 和 0(二进制值)。数字信号不如模拟信号准确,因为它们是在一段时间内采集的模拟信号的离散样本。然而,数字信号不会受到噪声的影响。因此它们持续时间长并且易于解释。数字信号用方波表示。
例如:
计算机键盘
每当从键盘按下一个键时,相应的电信号就会发送到包含该特定键的 ASCII 值的键盘控制器。例如按下键盘按键a时产生的电信号,以0和1的形式携带数字97的信息,即字符a的ASCII值。
模拟信号和数字信号的区别
| 比较元素 | 模拟信号 | 数字信号 |
|---|---|---|
| 分析 | 难的 | 可分析 |
| 表示 | 连续的 | 不连续 |
| 准确性 | 更准确 | 不太准确 |
| 贮存 | 无限内存 | 易于存放 |
| 受噪音影响 | 是的 | 不 |
| 录音技巧 | 保留原始信号 | 采集并保存信号样本 |
| 例子 | 人声、温度计、模拟电话等 | 电脑、数码电话、数码笔等 |
系统
系统是由它处理的输入和输出类型定义的。由于我们正在处理信号,因此在我们的例子中,我们的系统将是一个数学模型,一段代码/软件,或一个物理设备,或一个黑匣子,其输入是信号并对该信号执行一些处理,输出是一个信号。输入称为激励,输出称为响应。

上图中显示了一个系统,其输入和输出都是信号,但输入是模拟信号。并且输出是数字信号。这意味着我们的系统实际上是一个将模拟信号转换为数字信号的转换系统。
让我们看看这个黑匣子系统的内部
模拟信号到数字信号的转换
因为有很多与模数转换相关的概念,反之亦然。我们将只讨论与数字图像处理相关的那些。转换中涉及两个主要概念。
采样
量化
采样
顾名思义,抽样可以定义为取样。在 x 轴上采集数字信号样本。抽样是对自变量进行的。对于这个数学方程:

对 x 变量进行采样。我们也可以说x轴(无限值)到数字的转换是在采样下完成的。
采样又分为上采样和下采样。如果 x 轴上的值范围较小,那么我们将增加值的样本。这称为上采样,反之亦然称为下采样
量化
顾名思义,量化可以定义为划分为量子(分区)。量化是根据因变量完成的。它与抽样相反。
对于这个数学方程 y = sin(x)
量化是在 Y 变量上完成的。它是在 y 轴上完成的。将 y 轴无限值转换为 1 、 0 、 -1 (或任何其他级别)称为量化。
这是将模拟信号转换为数字信号时涉及的两个基本步骤。
信号的量化如下图所示。

为什么我们需要将模拟信号转换为数字信号。
第一个也是显而易见的原因是数字图像处理处理的是数字图像,即数字信号。因此,每当捕获图像时,都会将其转换为数字格式,然后进行处理。
第二个也是重要的原因是,为了使用数字计算机对模拟信号执行操作,您必须将该模拟信号存储在计算机中。为了存储模拟信号,需要无限的存储器来存储它。既然这是不可能的,所以这就是为什么我们将该信号转换为数字格式,然后将其存储在数字计算机中,然后对其进行运算。
连续系统与离散系统
连续系统
输入和输出均为连续信号或模拟信号的系统称为连续系统。

离散系统
输入和输出均为离散信号或数字信号的系统称为数字系统

摄影史
相机的由来
相机和摄影的历史并不完全相同。相机的概念在摄影概念出现之前就已经被引入很多次了
照相暗盒
相机的历史在于亚洲。相机的原理最早是由中国哲学家墨子提出的。它被称为暗箱。相机就是根据这一原理发展而来的。
暗箱一词是由两个不同的词演变而来的。相机和暗箱。相机这个词的意思是房间或某种拱顶,Obscura 代表黑暗。
这位中国哲学家提出的概念包括一种装置,可以将周围环境的图像投射到墙上。然而它不是中国人建造的。

暗箱的创建
汉语的概念是由穆斯林科学家阿布·阿里·哈桑·伊本·海瑟姆(Abu Ali Al-Hassan Ibn al-Haitham,俗称伊本·海瑟姆)带入现实的。他建造了第一台暗箱。他的相机遵循针孔相机的原理。他在大约 1000 个地方建造了这个设备。
便携式相机
1685 年,Johann Zahn 制造了第一台便携式相机。在这种设备出现之前,相机需要占用一定的空间并且不便于携带。尽管爱尔兰科学家罗伯特·博伊尔和罗伯特·胡克制造了一种可移动相机的设备,但该设备仍然非常巨大,无法将其从一个地方带到另一个地方。
摄影的起源
虽然暗箱是1000年由一位穆斯林科学家制造的。但它的第一次实际使用是在 13 世纪由英国哲学家罗杰·培根描述的。罗杰建议使用相机来观测日食。
达芬奇
尽管在15世纪之前已经取得了很大的改进,但列奥纳多·迪·皮耶罗·达·芬奇所做的改进和发现是引人注目的。达芬奇是一位伟大的艺术家、音乐家、解剖学家和战争工程师。他因许多发明而受到赞誉。他最著名的画作之一包括《蒙娜丽莎》。

达芬奇不仅按照针孔相机的原理制造了暗箱,而且还用它作为他的艺术作品的绘画辅助工具。在大西洋法典中描述的他的工作中,定义了暗箱的许多原理。

他的相机遵循针孔相机的原理,可以描述为
当被照亮的物体的图像穿过一个小孔进入一个非常黑暗的房间时,您将在[对面的墙上]看到这些物体以其适当的形式和颜色,由于光线的交叉而在相反的位置缩小尺寸。
第一张照片
第一张照片由法国发明家 Joseph Nicephore Niepce 于 1814 年拍摄。他在 Le Gras 的窗户上拍摄了第一张照片,方法是在锡盘上涂上沥青,然后将锡盘暴露在光线下。

第一张水下照片
第一张水下照片是由英国数学家威廉·汤姆森使用防水盒拍摄的。这是在 1856 年完成的。

电影的起源
电影的起源是由美国发明家、慈善家乔治·伊士曼介绍的,他被认为是摄影的先驱。
他创立了伊士曼柯达公司,以冲洗胶片而闻名。该公司于 1885 年开始生产纸质胶片。他首先发明了柯达相机,后来又发明了布朗尼相机。Brownie是一款盒式相机,因其快照功能而广受欢迎。

电影问世后,相机行业再次繁荣起来,一项发明催生了另一项发明。
徕卡和阿格斯
Leica和Argus是分别于1925年和1939年开发的两款模拟相机。徕卡相机是使用 35 毫米电影胶片制造的。

Argus是另一款采用35mm格式的模拟相机,与徕卡相比价格相当便宜,因此非常受欢迎。

模拟闭路电视摄像机
1942 年,德国工程师 Walter Bruch 开发并安装了第一个模拟闭路电视摄像机系统。他还因 1960 年彩色电视的发明而受到赞誉。
摄影包
第一台一次性相机由 Photo Pac 于 1949 年推出。该相机只是一次性相机,里面已经装有一卷胶卷。后来版本的 Photo pac 具有防水功能,甚至还配备了闪光灯。

数码相机
索尼 Mavica
Mavica(磁性摄像机)由索尼于 1981 年推出,是数码相机领域的第一款游戏规则改变者。图像记录在软盘上,以后可以在任何监视器屏幕上查看图像。
它不是纯粹的数码相机,而是模拟相机。但由于其在软盘上存储图像的能力而受到欢迎。这意味着您现在可以长期存储图像,并且可以在软盘上保存大量图片,当它们装满时,这些图片将被新的空白光盘替换。Mavica 的磁盘容量可存储 25 张图像。
mavica推出的另一件重要的事情是其0.3兆像素的照片拍摄能力。

数码相机
1988 年富士胶片推出的Fuji DS-1P 相机是第一台真正的数码相机
尼康 D1是一款 2.74 兆像素相机,也是尼康开发的第一款商用数码单反相机,对于专业人士来说非常实惠。

如今,手机中配备了数码相机,具有非常高的分辨率和质量。
应用与使用
由于数字图像处理的应用非常广泛,几乎所有的技术领域都受到DIP的影响,因此我们只讨论DIP的一些主要应用。
数字图像处理不仅仅限于调整相机拍摄的日常图像的空间分辨率。它不仅仅局限于增加照片的亮度等而是远远不止于此。
电磁波可以被认为是粒子流,其中每个粒子都以光速移动。每个粒子都包含一束能量。这束能量称为光子。
根据光子能量的电磁波谱如下所示。

在这个电磁光谱中,我们只能看到可见光谱。可见光谱主要包括七种不同的颜色,通常称为(VIBGOYR)。VIBGOYR 代表紫色、靛蓝、蓝色、绿色、橙色、黄色和红色。
但这并不能消除频谱中其他物质的存在。我们的人眼只能看到可见部分,在其中我们看到了所有物体。但相机可以看到肉眼无法看到的其他东西。例如:x 射线、伽马射线等,因此所有这些东西的分析也是在数字图像处理中完成的。
这个讨论引出了另一个问题,那就是
为什么我们还需要分析电磁频谱中的所有其他内容?
这个问题的答案在于事实,因为X射线等其他东西已经广泛应用于医疗领域。伽马射线的分析是必要的,因为它广泛应用于核医学和天文观测。电磁频谱中的其他事物也是如此。
数字图像处理的应用
下面提到数字图像处理广泛应用的一些主要领域
图像锐化和恢复
医疗领域
遥感
传输与编码
机器/机器人视觉
色彩处理
模式识别
视频处理
显微成像
其他的
图像锐化和恢复
图像锐化和恢复在这里指的是处理从现代相机捕获的图像以使其成为更好的图像或以达到期望结果的方式操纵这些图像。它指的是做 Photoshop 通常做的事情。
这包括缩放、模糊、锐化、灰度到颜色转换、检测边缘(反之亦然)、图像检索和图像识别。常见的例子有:
原始图像

缩放后的图像

图像模糊

图像清晰

边缘

医疗领域
DIP在医疗领域的常见应用是
伽马射线成像
正电子发射断层扫描
X 射线成像
医学CT
紫外成像
紫外成像
在遥感领域,通过卫星或从很高的地面扫描地球区域,然后对其进行分析以获得有关该区域的信息。数字图像处理在遥感领域的一项特殊应用是检测地震造成的基础设施损坏。
因为即使关注严重的损害,也需要更长的时间才能掌握损害。由于地震影响的区域有时非常广泛,以至于无法用肉眼检查来估计损失。即使是这样,这也是一个非常忙碌且耗时的过程。因此,在数字图像处理中找到了解决方案。从地面捕获受影响区域的图像,然后对其进行分析以检测地震造成的各种类型的损坏。

分析中的关键步骤是
边缘的提取
各类边缘分析与增强
传输与编码
第一张通过电线传输的图像是通过海底电缆从伦敦传输到纽约的。发送的图片如下所示。

发送的照片从一个地方到另一个地方花了三个小时。
现在想象一下,今天我们能够看到实时视频,或从一个大陆到另一个大陆的实时闭路电视录像,只需延迟几秒钟。这意味着在这个领域也已经做了很多工作。这个领域不仅仅关注传输,还关注编码。已经开发了许多不同的格式用于高或低带宽来编码照片,然后通过互联网等进行流式传输
机器/机器人视觉
除了当今机器人面临的许多挑战之外,最大的挑战之一仍然是增加机器人的视野。让机器人能够看到事物、识别事物、识别障碍等。这个领域已经做出了很多工作,并且已经引入了计算机视觉的完整其他领域来研究它。
障碍检测
障碍检测是通过图像处理完成的常见任务之一,通过识别图像中不同类型的物体,然后计算机器人和障碍之间的距离。

巡线机器人
如今大多数机器人都是沿着线路工作,因此被称为巡线机器人。这有助于机器人在其路径上移动并执行一些任务。这也是通过图像处理实现的。

色彩处理
颜色处理包括对彩色图像和所使用的不同颜色空间的处理。例如RGB颜色模型、YCbCr、HSV。它还涉及研究这些彩色图像的传输、存储和编码。
模式识别
模式识别涉及图像处理和包括机器学习(人工智能的一个分支)在内的各个其他领域的研究。在模式识别中,图像处理用于识别图像中的对象,然后使用机器学习来训练系统以适应模式的变化。模式识别用于计算机辅助诊断、手写识别、图像识别等。
视频处理
视频只不过是图片的快速移动。视频的质量取决于每分钟的帧/图片数量以及所使用的每帧的质量。视频处理涉及降噪、细节增强、运动检测、帧率转换、长宽比转换、色彩空间转换等。
维度的概念
我们将看这个例子来理解维度的概念。

假设你有一个住在月球上的朋友,他想在你的生日礼物上送给你一份礼物。他询问你在地球上的居住地。唯一的问题是月球上的快递服务不理解字母地址,而只理解数字坐标。那么你如何向他发送你在地球上的位置呢?
这就是维度的概念。尺寸定义了指向空间内任何特定对象的位置所需的最小点数。
让我们再次回到我们的示例,您必须将您在地球上的位置发送给您在月球上的朋友。您向他发送三对坐标。第一个称为经度,第二个称为纬度,第三个称为海拔。
这三个坐标定义了您在地球上的位置。前两个定义您的位置,第三个定义您的海拔高度。
这意味着只需要三个坐标即可定义您在地球上的位置。这意味着你生活在 3 维的世界中。因此,这不仅回答了关于维度的问题,还回答了我们生活在 3D 世界的原因。
由于我们正在参考数字图像处理来研究这个概念,因此我们现在将把这个尺寸概念与图像联系起来。
图像尺寸
因此,如果我们生活在 3D 世界,即 3 维世界,那么我们捕捉到的图像的尺寸是多少。图像是二维的,这就是为什么我们也将图像定义为二维信号。图像只有高度和宽度。图像没有深度。看看下面这张图片。

如果你看一下上图,它表明它只有两个轴,即高度和宽度轴。您无法从该图像中感知深度。这就是为什么我们说图像是二维信号。但是我们的眼睛能够感知三维物体,但这将在下一个关于相机如何工作以及图像如何被感知的教程中进行更多解释。
这个讨论引出了一些其他问题,即三维系统是如何从二维形成的。
电视是如何运作的?
如果我们看上面的图像,我们会发现它是一个二维图像。为了将其转换为三维,我们需要另一个维度。让我们将时间作为第三维度,在这种情况下,我们将在第三维度时间上移动这个二维图像。与电视中发生的概念相同,它可以帮助我们感知屏幕上不同物体的深度。这是否意味着电视上出现的内容或我们在电视屏幕上看到的内容都是 3D 的。好吧,我们可以。原因是,对于电视来说,我们正在播放视频。那么视频只不过是随时间维度移动的二维图片。由于二维物体在三维空间(时间)上移动,所以我们可以说它是三维的。
信号的不同维度
一维信号
一维信号的常见示例是波形。它可以在数学上表示为
F(x) = 波形
其中 x 是自变量。因为它是一维信号,所以这就是为什么只使用一个变量 x 。
一维信号的图示如下:

上图显示了一个一维信号。
现在这又引出了另一个问题,即尽管它是一维信号,但为什么它有两个轴?这个问题的答案是,尽管它是一维信号,但我们是在二维空间中绘制它。或者我们可以说我们表示该信号的空间是二维的。这就是为什么它看起来像二维信号。
也许看下图你可以更好地理解一维的概念。

现在回到我们最初关于维度的讨论,将上图视为一条从一点到另一点的正数实线。现在,如果我们必须解释这条线上任何点的位置,我们只需要一个数字,这意味着只有一维。
二维信号
二维信号的常见示例是图像,上面已经讨论过。

正如我们已经看到的,图像是二维信号,即:它具有二维。它可以在数学上表示为:
F (x, y) = 图像
其中 x 和 y 是两个变量。二维的概念也可以用数学来解释:

现在在上图中,将正方形的四个角分别标记为A、B、C和D。如果我们称图中的一条线段为AB,另一条线段为CD,那么我们可以看到这两条平行线段连接起来形成一个正方形。每条线段对应一维,因此这两条线段对应二维。
3维信号
三维信号顾名思义是指具有三个维度的信号。最常见的例子已经在开始时讨论过,那就是我们的世界。我们生活在一个三维世界。这个例子已经被非常详细地讨论过。三维信号的另一个示例是立方体或体积数据,或者最常见的示例是动画或 3D 卡通人物。
三维信号的数学表示为:
F(x,y,z) = 动画角色。
另一个轴或维度 Z 涉及三维空间,这给出了深度的错觉。在笛卡尔坐标系中,它可以被视为:

4维信号
在四维信号中,涉及四个维度。前三个与三维信号相同,分别是:(X,Y,Z),第四个与它们相加是T(时间)。时间通常被称为时间维度,是衡量变化的一种方式。从数学上讲,四维信号可以表示为:
F(x,y,z,t) = 动画电影。
4 维信号的常见示例可以是动画 3D 电影。由于每个角色都是 3D 角色,因此他们会随着时间而移动,因此我们看到了 3D 电影的幻觉,更像是真实世界。
所以这意味着实际上动画电影是 4 维的,即:3D 角色在第四维时间上的运动。
相机成像
人眼是如何工作的?
在我们讨论模拟和数码相机上的成像之前,我们必须首先讨论人眼上的成像。因为相机遵循的基本原理是从人眼的工作方式中获取的。
当光照射到特定物体上时,光线穿过该物体后会反射回来。光线通过眼睛的晶状体时,形成特定的角度,并在位于墙壁背面的视网膜上形成图像。形成的图像是倒置的。然后大脑解释该图像,使我们能够理解事物。由于角度的形成,我们能够感知我们所看到的物体的高度和深度。这在透视变换教程中有更多解释。

从上图中可以看出,当太阳光照射到物体上(本例中物体是人脸)时,光线被反射回来,不同的光线通过镜头时会形成不同的角度,形成如下的倒像:该物体已在后墙上形成。该图的最后部分表示该物体已被大脑解释并重新反转。
现在让我们回到模拟和数码相机的图像形成上来讨论。
模拟相机上的图像形成

在模拟相机中,图像的形成是由于用于图像形成的条带上发生的化学反应所致。
35mm条带用于模拟相机。图中用35mm胶片暗盒表示。该条带涂有卤化银(一种化学物质)。

35mm条带用于模拟相机。图中用35mm胶片暗盒表示。该条带涂有卤化银(一种化学物质)。
光只不过是被称为光子粒子的小粒子。因此,当这些光子粒子通过相机时,它会与条带上的卤化银粒子发生反应,产生银色,即图像的负片。
为了更好地理解它,请看一下这个方程。
光子(光粒子)+卤化银?银 ?图像负片。

这只是基础知识,尽管图像形成涉及许多其他有关内部光线通过的概念,以及快门和快门速度以及光圈及其开口的概念,但现在我们将继续下一部分。尽管大多数概念已经在我们的快门和光圈教程中讨论过。
这只是基础知识,尽管图像形成涉及许多其他有关内部光线通过的概念,以及快门和快门速度以及光圈及其开口的概念,但现在我们将继续下一部分。尽管大多数概念已经在我们的快门和光圈教程中讨论过。
数码相机上的图像形成
在数码相机中,图像的形成不是由于发生的化学反应造成的,而是比这更复杂一些。在数码相机中,CCD 传感器阵列用于形成图像。
通过 CCD 阵列成像

CCD 代表电荷耦合器件。它是一个图像传感器,与其他传感器一样,它感测值并将其转换为电信号。如果是 CCD,它会感测图像并将其转换为电信号等
这种CCD实际上是阵列或矩形网格的形状。它就像一个矩阵,矩阵中的每个单元都包含一个感测光子强度的检查器。

与模拟相机一样,数字相机也是如此,当光线照射到物体上时,光线在撞击物体后会反射回来并进入相机内部。
CCD阵列本身的每个传感器都是模拟传感器。当光子撞击芯片时,每个光传感器中都会保留少量电荷。每个传感器的响应直接等于照射到传感器表面的光或(光子)能量的量。
由于我们已经将图像定义为二维信号,并且由于 CCD 阵列的二维形成,因此可以从该 CCD 阵列获得完整的图像。
它的传感器数量有限,这意味着它可以捕获的细节有限。此外,每个传感器对于撞击其上的每个光子粒子只能有一个值。
因此,计算并存储撞击(当前)的光子数量。为了准确测量这些,外部 CMOS 传感器还附加了 CCD 阵列。
像素简介
CCD阵列的每个传感器的值是指每个单独像素的值。传感器数量=像素数量。这也意味着每个传感器只能有一个且只有一个值。
存储图像
CCD 阵列存储的电荷每次转换为一个像素的电压。在附加电路的帮助下,该电压被转换成数字信息,然后被存储。
每家生产数码相机的公司都生产自己的 CCD 传感器。其中包括索尼、三菱、尼康、三星、东芝、富士、佳能等
除了其他因素外,捕获图像的质量还取决于所使用的 CCD 阵列的类型和质量。
摄像机构
在本教程中,我们将讨论一些基本的相机概念,例如光圈、快门、快门速度、ISO,并且我们将讨论如何集体使用这些概念来捕捉优质图像。
光圈
光圈是一个小开口,可让光线进入相机内部。这是光圈的图片。

你会在光圈内看到一些小刀片,就像东西一样。这些刀片形成可以打开或关闭的八角形形状。因此,打开的叶片越多,光线必须通过的孔就会越大,这是有道理的。孔越大,允许进入的光就越多。
影响
光圈的效果直接对应于图像的亮度和暗度。如果光圈开口较宽,则可以让更多的光线进入相机。更多的光会产生更多的光子,最终产生更明亮的图像。
其示例如下所示
考虑这两张照片


右边的看起来更亮,说明相机拍摄时光圈是全开的。与左侧的另一张图片相比,该图片比第一张图片非常暗,这表明拍摄该图像时,其光圈并未全开。
尺寸
现在让我们讨论光圈背后的数学原理。光圈的大小用af值表示。并且与光圈开度成反比。
这是最好地解释这个概念的两个方程。
大光圈=小f值
小孔径=更大的f值
形象地说,它可以表示为:

快门
光圈之后就是快门。当光线从光圈穿过时,直接落在快门上。百叶窗实际上是一个盖子,一扇关闭的窗户,或者可以认为是一个窗帘。还记得我们谈论形成图像的 CCD 阵列传感器吗?快门后面是传感器。因此,当光线通过光圈时,快门是图像形成和光线之间的唯一物体。
一旦快门打开,光线就会落在图像传感器上,图像就会形成在阵列上。
影响
如果快门允许光线通过的时间长一点,图像就会更亮。同样,当允许快门快速移动时,会产生较暗的图像,因此,允许通过的光的光子非常少,并且在 CCD 阵列传感器上形成的图像非常暗。
Shutter 还有两个主要概念:
快门速度
快门时间
快门速度
快门速度可以指快门打开或关闭的次数。请记住,我们不是在谈论快门打开或关闭多长时间。
快门时间
快门时间可以定义为
当快门打开时,直到快门关闭所需的等待时间称为快门时间。
在这种情况下,我们不是在谈论快门打开或关闭多少次,而是在谈论它保持完全打开的时间。
例如:
这样我们就可以更好的理解这两个概念。假设快门打开 15 次然后关闭,每次打开 1 秒然后关闭。在此示例中,15 是快门速度,1 秒是快门时间。
关系
快门速度和快门时间之间的关系是两者成反比。
这种关系可以用下面的等式来定义。
更高的快门速度 = 更短的快门时间
较低的快门速度=较长的快门时间。
解释:
所需时间越少,速度越快。并且所需的时间越长,速度就越慢。
应用领域
这两个概念共同构成了多种应用。下面给出了其中一些。
快速移动的物体:
如果您要捕捉快速移动物体的图像,可以是汽车或任何物体。快门速度及其时间的调整影响很大。
因此,为了捕获这样的图像,我们将进行两处修改:
提高快门速度
减少快门时间
发生的情况是,当我们提高快门速度时,快门打开或关闭的次数越多。这意味着不同的光线样本将允许进入。当我们减少快门时间时,这意味着我们将立即捕捉场景,并关闭快门门。
如果您这样做,您将获得快速移动物体的清晰图像。
为了理解它,我们将看这个例子。假设您想捕捉快速移动的瀑布的图像。
您将快门速度设置为 1 秒并拍摄照片。这就是你得到的

然后你将快门速度设置为更快的速度,你就得到了。

然后你再次将快门速度设置得更快,你就得到了。

您可以在最后一张图片中看到,我们将快门速度提高到非常快,这意味着快门在 1 秒的 200 秒内打开或关闭,因此我们得到了清晰的图像。
国际标准化组织
ISO 系数以数字来衡量。它表示光线对相机的敏感度。如果 ISO 值较低,则意味着我们的相机对光线较不敏感;如果 ISO 值较高,则意味着它更敏感。
影响
ISO 越高,图像越亮。如果ISO设置为1600,图片会非常亮,反之亦然。
副作用
如果 ISO 增加,图像中的噪点也会增加。如今,大多数相机制造公司都致力于在 ISO 设置为更高速度时消除图像中的噪点。
像素的概念
像素
像素是图像的最小元素。每个像素对应于任何一个值。在 8 位灰度图像中,像素的值在 0 到 255 之间。任意点的像素值对应于撞击该点的可见光子的强度。每个像素存储一个与该特定位置的光强度成比例的值。
佩尔
像素也称为 PEL。您可以通过下面给出的图片对像素有更多的了解。
在上图中,可能有数千个像素,它们共同构成了这张图像。我们将该图像缩放到能够看到一些像素划分的程度。如下图所示。

在上图中,可能有数千个像素,它们共同构成了这张图像。我们将该图像缩放到能够看到一些像素划分的程度。如下图所示。
与CCD阵列的关系
我们已经了解了 CCD 阵列中图像是如何形成的。所以一个像素也可以定义为
CCD 阵列的最小划分也称为像素。
CCD 阵列的每个分区都包含与撞击它的光子强度相对应的值。该值也可以称为像素

总像素数的计算
我们将图像定义为二维信号或矩阵。那么在这种情况下,PEL 的数量将等于行数乘以列数。
这可以用数学方式表示如下:
总像素数 = 行数 ( X ) 列数
或者我们可以说 (x,y) 坐标对的数量构成了像素的总数。
我们将在图像类型教程中更详细地了解如何计算彩色图像中的像素。
灰度级
任意点的像素值表示该位置图像的强度,也称为灰度级。
我们将更详细地了解图像存储中的像素值和每像素位数教程,但现在我们只讨论一个像素值的概念。
像素值。(0)
正如本教程一开始就已经定义的那样,每个像素只能有一个值,每个值表示图像该点的光强度。
现在我们来看一个非常独特的值 0。值 0 表示没有光。这意味着 0 表示暗,进一步意味着当一个像素的值为 0 时,就意味着在该点将形成黑色。
看看这个图像矩阵
| 0 | 0 | 0 |
| 0 | 0 | 0 |
| 0 | 0 | 0 |
现在这个图像矩阵已经全部填满了 0。所有像素的值为 0。如果我们要计算这个矩阵的像素总数,这就是我们要做的。
总像素数 = 总像素数 行数 X 总数 列数
= 3 × 3
= 9。
这意味着图像将由 9 个像素形成,并且该图像的尺寸为 3 行和 3 列,最重要的是该图像将是黑色的。
生成的图像将是这样的

现在为什么这张图片全黑了。因为图像中所有像素的值为 0。
视角转换
当人的眼睛看近处的东西时,与看远处的东西相比,它们看起来更大。一般而言,这称为透视。而转换是将对象等从一种状态转移到另一种状态。
总的来说,透视变换涉及将 3D 世界转换为 2D 图像。人类视觉的工作原理和相机的工作原理相同。
我们将详细了解为什么会发生这种情况,那些靠近你的物体看起来更大,而那些远处的物体看起来更小,尽管当你到达它们时它们看起来更大。
我们将从参考系的概念开始讨论:
参照系:
参考系基本上是一组与我们测量某些事物相关的值。

5个参考系
为了分析 3D 世界/图像/场景,需要 5 个不同的参考系。
目的
世界
相机
图像
像素
物体坐标系
对象坐标系用于对对象进行建模。例如,检查特定对象相对于另一个对象是否位于正确的位置。它是一个 3d 坐标系。
世界坐标系
世界坐标系用于关联 3 维世界中的对象。它是一个 3d 坐标系。
相机坐标系
相机坐标系用于将对象与相机相关联。它是一个 3d 坐标系。
图像坐标系
它不是 3d 坐标系,而是 2d 系统。它用于描述 3d 点如何映射到 2d 图像平面。
像素坐标系
它也是一个二维坐标系。每个像素都有一个像素坐标值。
这5个框架之间的变换

这就是将 3D 场景转换为 2D 场景(带有像素图像)的方式。
现在我们将从数学上解释这个概念。
 在哪里
在哪里
Y = 3d 对象
y = 二维图像
f = 相机的焦距
Z = 图像与相机之间的距离
现在这个变换中形成了两个不同的角度,用 Q 表示。
第一个角度是

其中负号表示图像反转。所形成的第二个角为:

比较这两个方程我们得到

从这个方程我们可以看出,光线从相机经过物体后反射回来,就形成了倒立的图像。
通过这个例子我们可以更好地理解这一点。
例如
计算形成图像的尺寸
假设拍摄了一个身高 5m 的人的图像,站在距离相机 50m 的位置,我们必须知道焦距为 50mm 的相机下该人的图像大小是多少。
解决方案:
由于焦距的单位是毫米,所以我们必须将所有内容都转换为毫米才能计算。
所以,
Y = 5000 毫米。
f = 50 毫米。
Z = 50000 毫米。
将值代入公式,我们得到

= -5 毫米。
同样,减号表示图像是倒置的。
每像素位数的概念
Bpp 或每像素位数表示每像素的位数。图像中不同颜色的数量取决于颜色的深度或每像素的位数。
数学中的位:
这就像玩二进制位一样。
一位可以表示多少个数字。
0
1
可以进行多少个两位组合。
00
01
10
11
如果我们设计一个公式来计算可以由 bit 组成的组合总数,那就是这样的。
其中 bpp 表示每像素位数。将 1 代入公式,得到 2,将 2 代入公式,得到 4。它呈指数增长。
不同颜色的数量:
正如我们一开始所说的,不同颜色的数量取决于每个像素的位数。
下面给出了一些位及其颜色的表格。
| 每像素位数 | 颜色数量 |
|---|---|
| 1 bp | 2种颜色 |
| 2位点 | 4种颜色 |
| 3 bpp | 8种颜色 |
| 4位点 | 16种颜色 |
| 5 bpp | 32种颜色 |
| 6位点 | 64种颜色 |
| 7 bp | 128种颜色 |
| 8 bp | 256色 |
| 10个基点 | 1024 种颜色 |
| 16 bpp | 65536 种颜色 |
| 24 bpp | 16777216 种颜色(1670 万种颜色) |
| 32 bpp | 4294967296 色(4294 百万色) |
该表显示了每个像素的不同位数以及它们包含的颜色量。
色调
您可以轻松注意到指数增长的模式。著名的灰度图像为 8 bpp ,意味着它有 256 种不同的颜色或 256 种色调。
阴影可以表示为:

彩色图像通常为 24 bpp 或 16 bpp 格式。
我们将在图像类型教程中了解有关其他颜色格式和图像类型的更多信息。
颜色值:
我们之前在像素概念教程中已经看到,0像素值表示黑色。黑色:
请记住,0 像素值始终表示黑色。但没有固定的值来表示白色。白色:
表示白色的值可以计算为:

在 1 bpp 的情况下,0 表示黑色,1 表示白色。
在 8 bpp 的情况下,0 表示黑色,255 表示白色。
灰色:
当计算出黑白颜色值时,就可以计算出灰色的像素值。
灰色实际上是黑色和白色的中间点。也就是说,
在 8bpp 的情况下,表示灰色的像素值为 127 或 128bpp(如果从 1 开始计数,而不是从 0 开始计数)。
图像存储要求
在讨论了每像素位数之后,现在我们已经有了计算图像大小所需的一切。
图片大小
图像的大小取决于三个因素。
行数
列数
每个像素的位数
下面给出了计算尺寸的公式。
图像大小 = 行数 * 列数 * bpp
这意味着如果你有一张图像,就说这个:

假设它有 1024 行和 1024 列。由于它是灰度图像,因此它有 256 种不同的灰度,或者说每像素有位数。然后将这些值代入公式,我们得到
图像大小 = 行数 * 列数 * bpp
= 1024 * 1024 * 8
= 8388608 位。
但由于它不是我们认可的标准答案,因此会将其转换为我们的格式。
将其转换为字节 = 8388608 / 8 = 1048576 字节。
转换为千字节 = 1048576 / 1024 = 1024kb。
转换为兆字节 = 1024 / 1024 = 1 Mb。
这就是图像尺寸的计算和存储方式。现在在公式中,如果给定图像的大小和每像素的位数,您还可以计算图像的行和列,前提是图像是正方形(相同的行和相同的列)。
图像类型
图像有很多类型,我们将详细了解不同类型的图像以及其中的颜色分布。
二值图像
顾名思义,二进制图像仅包含两个像素值。
0 和 1。
在我们之前的每像素位数教程中,我们已经详细解释了像素值及其各自颜色的表示。
这里0代表黑色,1代表白色。它也称为单色。
黑白图像:
因此形成的最终图像仅由黑色和白色组成,因此也可以称为黑白图像。

无灰度级
该二值图像的有趣之处之一是其中没有灰度级。其中只有黑色和白色两种颜色。
格式
二进制图像的格式为 PBM(便携式位图)
2 , 3 , 4 ,5 ,6 位颜色格式
2、3、4、5 和 6 位颜色格式的图像目前尚未广泛使用。它们在过去用于旧电视显示器或监视器显示器。
但这些颜色中的每一种都具有两个以上的灰度级,因此与二值图像不同,具有灰色。
在2位4中、在3位8中、在4位16中、在5位32中、在6位64中存在不同的颜色。
8 位颜色格式
8 位颜色格式是最著名的图像格式之一。它有 256 种不同深浅的颜色。它通常被称为灰度图像。
8 位颜色的范围为 0-255。其中 0 代表黑色,255 代表白色,127 代表灰色。
这种格式最初由早期的 UNIX 操作系统模型和早期的彩色 Macintoshes 使用。
爱因斯坦的灰度图像如下所示:

格式
这些图像的格式是PGM(便携式灰度图)。
Windows 默认不支持此格式。为了查看灰度图像,您需要有图像查看器或图像处理工具箱,例如Matlab。
灰度图像背后:
正如我们在之前的教程中多次解释过的那样,图像只不过是一个二维函数,并且可以用二维数组或矩阵来表示。因此,在上面显示的爱因斯坦图像的情况下,后面会有一个二维矩阵,其值范围在 0 到 255 之间。
但彩色图像的情况并非如此。
16 位颜色格式
它是一种彩色图像格式。它有 65,536 种不同的颜色。它也称为高色彩格式。
Microsoft 已在支持 8 位以上颜色格式的系统中使用它。现在这个 16 位格式和我们要讨论的下一个格式(24 位格式)都是彩色格式。
彩色图像中的颜色分布并不像灰度图像中那样简单。
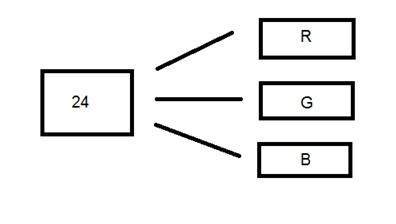
16 位格式实际上又分为三种格式:红、绿、蓝。著名的(RGB)格式。
如下图所示。

现在问题来了,如何将 16 分成三份。如果你这样做的话
R 5 位,G 5 位,B 5 位
那么最后还剩下一点。
那么16位的分配就这样完成了。
R 为 5 位,G 为 6 位,B 为 5 位。
留下的额外位被添加到绿色位中。因为绿色是这三种颜色中最舒缓眼睛的颜色。
请注意,并非所有系统都遵循此分布。有些在 16 位中引入了 Alpha 通道。
另一种16位格式的分布是这样的:
4 位用于 R ,4 位用于 G ,4 位用于 B ,4 位用于 Alpha 通道。
或者有些人像这样分发它
R 为 5 位,G 为 5 位,B 为 5 位,Alpha 通道为 1 位。
24 位颜色格式
24 位颜色格式也称为真彩色格式。与 16 位颜色格式一样,在 24 位颜色格式中,24 位又以红、绿、蓝三种不同的格式分布。
由于 24 在 8 上均分,因此它已平均分配在三个不同的颜色通道之间。
他们的分布是这样的。
R 为 8 位,G 为 8 位,B 为 8 位。
在 24 位图像后面。
与 8 位灰度图像后面只有一个矩阵不同,24 位图像具有 R、G、B 三个不同的矩阵。

格式
它是最常用的格式。其格式为Linux操作系统支持的PPM(Portable pixMap)。著名的Windows有自己的格式,即BMP(位图)。
颜色代码转换
在本教程中,我们将看到如何将不同的颜色代码组合成其他颜色,以及如何隐藏 RGB 颜色