图像转换

---

在讨论什么是图像变换之前，我们先讨论什么是变换。

转型

变换是一个函数。在执行某些操作后将一个集合映射到另一个集合的函数。

数字图像处理系统

我们已经在入门教程中看到，在数字图像处理中，我们将开发一个系统，其输入是图像，输出也是图像。系统会对输入图像进行一些处理，并将其输出作为处理后的图像。如下所示。

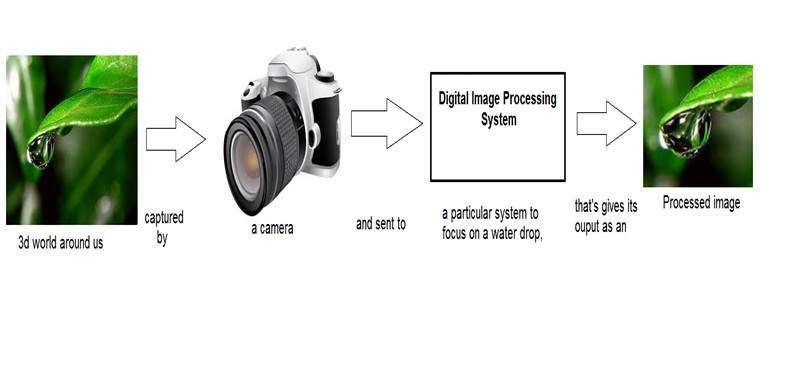
现在，在该数字系统中应用的处理图像并将其转换为输出的函数可以称为变换函数。

因为它显示了变换或关系，即图像 1 如何转换为图像 2。

图像变换。

考虑这个方程

G(x,y) = T{ f(x,y) }

在这个等式中，

F(x,y) = 必须应用变换函数的输入图像。

G(x,y) = 输出图像或处理后的图像。

T是变换函数。

输入图像和处理后的输出图像之间的这种关系也可以表示为

s = T (r)

其中r实际上是f(x,y)在任意点的像素值或灰度级强度。s是g(x,y)在任意点的像素值或灰度级强度。

基本灰度变换已在我们的基本灰度变换教程中讨论过。

现在我们将讨论一些非常基本的转换函数。

例子

考虑这个变换函数。

让我们将点 r 设为 256，将点 p 设为 127。将此图像视为 1 bpp 图像。这意味着我们只有两个强度级别，即 0 和 1。因此在这种情况下，图所示的变换可以解释为：

所有低于 127（p 点）的像素强度值均为 0，表示黑色。所有大于 127 的像素强度值均为 1，即白色。但在 127 的精确点上，传输发生了突然变化，因此我们无法判断在该精确点上该值是 0 还是 1。

从数学上讲，这个变换函数可以表示为：

考虑另一个像这样的转换

现在，如果您查看这个特定的图表，您将看到输入图像和输出图像之间的直线过渡线。

它表明对于输入图像的每个像素或强度值，输出图像都有相同的强度值。这意味着输出图像是输入图像的精确复制品。

它可以在数学上表示为：

g(x,y) = f(x,y)

在这种情况下，输入和输出图像如下所示。