设计与分析 - 分而治之

使用分而治之的方法，将手头的问题分成更小的子问题，然后独立解决每个问题。当我们不断地将子问题划分为更小的子问题时，我们最终可能会达到无法再划分的阶段。这些最小的可能子问题是使用原始解决方案来解决的，因为它需要更少的计算时间。最后将所有子问题的解进行合并，得到原问题的解。

从广义上讲，我们可以通过三步过程来理解分而治之的方法。

此步骤涉及将问题分解为更小的子问题。子问题应该代表原始问题的一部分。这一步一般采用递归的方式来划分问题，直到没有子问题可进一步整除为止。在此阶段，子问题的大小变得Atomics，但仍然代表实际问题的某些部分。

这一步接收到许多需要解决的较小的子问题。一般来说，在这个级别上，问题被认为是自行“解决”的。

当较小的子问题得到解决后，此阶段会递归地组合它们，直到它们形成原始问题的解决方案。这种算法方法以递归方式工作，并且征服和合并步骤的工作方式非常接近，以至于它们看起来像是一个整体。

数组作为输入

各种算法可以采用多种方式获取输入，以便可以使用分而治之技术来解决它们。数组就是其中之一。在需要输入为列表形式的算法中，如各种排序算法，最常用的是数组数据结构。

在下面的排序算法的输入中，数组输入被划分为子问题，直到它们无法进一步划分为止。

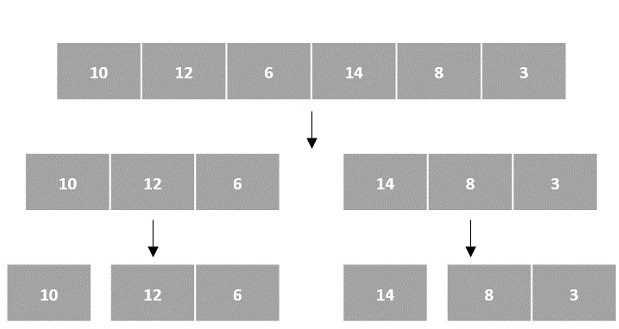
然后，对子问题进行排序（征服步骤）并合并以形成原始数组的解决方案（组合步骤）。

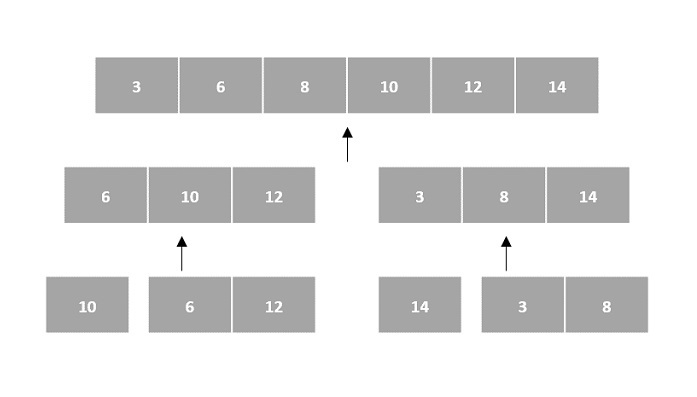
由于数组是索引和线性数据结构，因此排序算法最普遍使用数组数据结构来接收输入。

另一种可用于为分而治之算法获取输入的数据结构是链表（例如，使用链表的合并排序）。与数组一样，链表也是顺序存储数据的线性数据结构。

考虑链表上的归并排序算法；按照非常流行的龟兔赛跑算法，对列表进行划分，直到不能再划分为止。

然后，对列表中的节点进行排序（征服）。然后递归地组合（或合并）这些节点，直到获得最终解决方案。

由于链表不是索引的线性数据结构，因此还可以使用稍微不同的技术对链表数据结构执行各种搜索算法。必须使用列表节点中可用的指针来处理它们。

分而治之的方法支持并行性，因为子问题是独立的。因此，使用这种技术设计的算法可以在多处理器系统上或同时在不同的机器上运行。

在这种方法中，大多数算法都是使用递归设计的，因此内存管理非常高。对于递归函数，使用堆栈，其中需要存储函数状态。

以下计算机算法基于分而治之的编程方法 -

解决任何计算机问题都有多种方法，但提到的方法是分而治之的一个很好的例子。