设计与分析 - Karatsuba 算法

系统使用Karatsuba 算法对两个n 位数字执行快速乘法，即系统编译器计算乘积所需的时间比普通乘法所花费的时间要少。

通常的乘法方法需要 n ^{2 次}计算才能获得最终的乘积，因为必须在两个数字中的所有数字组合之间执行乘法，然后将子乘积相加以获得最终的乘积。这种乘法方法称为朴素乘法。

为了更好地理解这种乘法，让我们考虑两个 4 位整数：1456和6533，并使用简单的方法求出乘积。

那么，1456 × 6533 =？

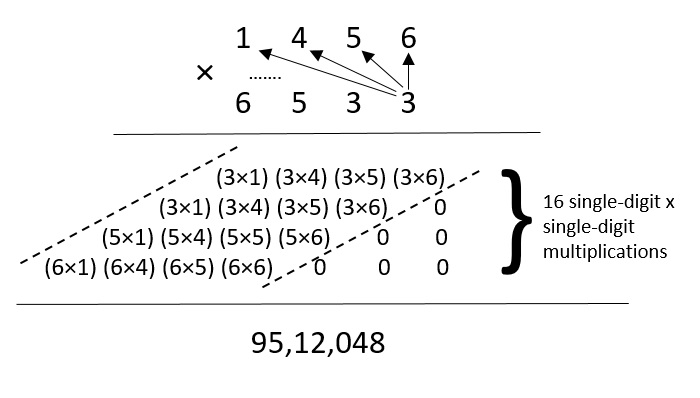
在这种朴素乘法方法中，假设两个数的位数都是 4，则执行 16 个个位数 × 个位数乘法。因此，该方法的时间复杂度为 O(4 ² )，因为它需要 4 ^{2 个}步骤来计算最终产品。

但当n的值不断增加时，问题的时间复杂度也不断增加。因此，采用Karatsuba算法来执行更快的乘法。

唐叶算法

Karasuba算法的主要思想是将多个子问题的乘法减少为三个子问题的乘法。加法和减法等算术运算用于其他计算。

对于该算法，将两个n位数字作为输入，并获得两个数字的乘积作为输出。

步骤 1 - 在此算法中，我们假设 n 是 2 的幂。

步骤 2 - 如果 n = 1，那么我们使用乘法表找到 P = XY。

步骤 3 - 如果 n > 1，则将 n 位数字分成两半并使用以下公式表示该数字 -

X = 10^n/2X₁ + X₂
Y = 10^n/2Y₁ + Y₂

其中，X ₁、X ₂、Y ₁、Y ₂各有n/2位。

步骤 4 - 取变量 Z = W – (U + V)，

在哪里，

U = X ₁ Y ₁ , V = X ₂ Y ₂
W = (X ₁ + X ₂ ) (Y ₁ + Y ₂ ), Z = X ₁ Y ₂ + X ₂ Y ₁。

步骤5 - 然后，将数值代入公式后得到乘积P -

P = 10ⁿ(U) + 10n/2(Z) + V
P = 10ⁿ (X₁Y₁) + 10n/2 (X₁Y₂ + X₂Y₁) + X₂Y₂.

步骤 6 - 通过分别传递子问题 (X ₁ , Y ₁ )、(X ₂ , Y ₂ ) 和 (X ₁ + X ₂ , Y ₁ + Y ₂ ) 递归调用算法。将返回值分别存储在变量 U、V 和 W 中。

例子

让我们使用 Karatsuba 方法解决上面给出的相同问题，1456 × 6533 -

Karatsuba 方法采用分而治之的方法，将问题划分为多个子问题，并应用递归来使乘法变得更简单。

步骤1

假设 n 是 2 的幂，将 n 位数字重写为 -

X = 10^n/2X₁ + X₂ Y = 10^n/2Y₁ + Y₂

这给了我们，

1456 = 10²(14) + 56 
6533 = 10²(65) + 33

首先让我们尝试简化数学表达式，我们得到，

(1400 × 6500) + (56 × 33) + (1400 × 33) + (6500 × 56) = 10⁴ (14 × 65) + 10² [(14 × 33) + (56 × 65)] + (33 × 56)

上面的表达式是给定乘法问题的简化版本，因为两个两位数相乘比两个四位数相乘更容易解决。

然而，这对于人类的思维来说也是如此。但对于系统编译器来说，上面的表达式仍然需要与普通朴素乘法相同的时间复杂度。由于它有 4 个两位数 × 两位数乘法，因此所需的时间复杂度为 -

14 × 65 → O(4)
14 × 33 → O(4)
65 × 56 → O(4)
56 × 33 → O(4)
= O (16)

因此，计算需要进一步简化。

第2步

X = 1456 
Y = 6533

由于 n 不等于 1，算法跳至步骤 3。

X = 10^n/2X₁ + X₂ 
Y = 10^n/2Y₁ + Y₂

这给了我们，

1456 = 10²(14) + 56 
6533 = 10²(65) + 33

计算 Z = W – (U + V) −

Z = (X₁ + X₂) (Y₁ + Y₂) – (X₁Y₁ + X₂Y₂) 
Z = X₁Y₂ + X₂Y₁ 
Z = (14 × 33) + (65 × 56)

最终产品，

P = 10ⁿ. U + 10^n/2. Z + V 
   = 10ⁿ (X₁Y₁) + 10^n/2 (X₁Y₂ + X₂Y₁) + X₂Y₂ 
   = 10⁴ (14 × 65) + 10² [(14 × 33) + (65 × 56)] + (56 × 33)

子问题可以进一步划分为更小的问题；因此，算法再次被递归调用。

步骤3

X ₁和 Y ₁作为参数 X 和 Y 传递。

所以现在，X = 14，Y = 65

X = 10^n/2X₁ + X₂ 
Y = 10^n/2Y₁ + Y₂ 
14 = 10(1) + 4 
65 = 10(6) + 5

计算 Z = W – (U + V) −

Z = (X₁ + X₂) (Y₁ + Y₂) – (X₁Y₁ + X₂Y₂) 
Z = X₁Y₂ + X₂Y₁ 
Z = (1 × 5) + (6 × 4) = 29 

P = 10ⁿ (X₁Y₁) + 10^n/2 (X₁Y₂ + X₂Y₁) + X₂Y₂ 
   = 10² (1 × 6) + 101 (29) + (4 × 5) 
   = 910

步骤4

X ₂和 Y ₂作为参数 X 和 Y 传递。

所以现在，X = 56，Y = 33

X = 10^n/2X₁ + X₂ 
Y = 10^n/2Y₁ + Y₂ 
56 = 10(5) + 6 
33 = 10(3) + 3

计算 Z = W – (U + V) −

Z = (X₁ + X₂) (Y₁ + Y₂) – (X₁Y₁ + X₂Y₂) 
Z = X₁Y₂ + X₂Y₁ 
Z = (5 × 3) + (6 × 3) = 33 

P = 10ⁿ (X₁Y₁) + 10^n/2 (X₁Y₂ + X₂Y₁) + X₂Y₂ 
= 10² (5 × 3) + 101 (33) + (6 × 3) 
= 1848

步骤5

X ₁ + X ₂和 Y ₁ + Y ₂作为参数 X 和 Y 传递。

所以现在，X = 70，Y = 98

X = 10^n/2X₁ + X₂ 
Y = 10^n/2Y₁ + Y₂ 
70 = 10(7) + 0 
98 = 10(9) + 8

计算 Z = W – (U + V) −

Z = (X₁ + X₂) (Y₁ + Y₂) – (X₁Y₁ + X₂Y₂) 
Z = X₁Y₂ + X₂Y₁ 
Z = (7 × 8) + (0 × 9) = 56 

P = 10ⁿ (X₁Y₁) + 10^n/2 (X₁Y₂ + X₂Y₁) + X₂Y₂ 
= 10² (7 × 9) + 101 (56) + (0 × 8) 
=

步骤6

最终产品，

P = 10ⁿ. U + 10^n/2. Z + V

U = 910 
V = 1848 
Z = W – (U + V) = 6860 – (1848 + 910) = 4102

代入方程中的值，

P = 10ⁿ. U + 10^n/2. Z + V 
P = 10⁴ (910) + 10² (4102) + 1848 
P = 91,00,000 + 4,10,200 + 1848 
P = 95,12,048

分析

Karasuba算法是一种递归算法；因为它在执行期间调用自身的较小实例。

根据该算法，它仅对 n/2 位数字调用自身三次，即可获得两个 n 位数字的最终乘积。

现在，如果 T(n) 表示执行乘法时所需的位数，

T(n) = 3T(n/2)

该方程是一个简单的递推关系，可以求解为 -

Apply T(n/2) = 3T(n/4) in the above equation, we get:
T(n) = 9T(n/4)
T(n) = 27T(n/8)
T(n) = 81T(n/16)
.
.
.
.
T(n) = 3ⁱ T(n/2ⁱ) is the general form of the recurrence relation of Karatsuba algorithm.

递归关系可以使用主定理来解决，因为我们有一个形式为的除法函数 -

T(n) = aT(n/b) + f(n), where, a = 3, b = 2 and f(n) = 0 which leads to k = 0.

由于 f(n) 表示在递归之外完成的工作，即 Karatsuba 中的加法和减法算术运算，因此这些算术运算不会增加时间复杂度。

^{检查“a”和“b k} ”之间的关系。

a > b^k = 3 > 2⁰

根据马斯特定理，应用情况1。

T(n) = O(n^{logb a})
T(n) = O(n^{log 3})

Karasuba 快速乘法算法的时间复杂度为O(n ^{log 3} )。

例子

在 Karatsuba 算法的完整实现中，我们尝试将两个更高值的数字相乘。在这里，由于long数据类型接受最多 18 位小数，因此我们将输入视为long值。递归调用Karatsuba函数，直到获得最终结果。

C C++ Java Python

#include <stdio.h>
#include <math.h>
int get_size(long);
long karatsuba(long X, long Y){
   
   // Base Case
   if (X < 10 && Y < 10)
      return X * Y;
   
   // determine the size of X and Y
   int size = fmax(get_size(X), get_size(Y));
   if(size < 10)
      return X * Y;
   
   // rounding up the max length
   size = (size/2) + (size%2);
   long multiplier = pow(10, size);
   long b = X/multiplier;
   long a = X - (b * multiplier);
   long d = Y / multiplier;
   long c = Y - (d * size);
   long u = karatsuba(a, c);
   long z = karatsuba(a + b, c + d);
   long v = karatsuba(b, d);
   return u + ((z - u - v) * multiplier) + (v * (long)(pow(10, 2 * size)));
}
int get_size(long value){
   int count = 0;
   while (value > 0) {
      count++;
      value /= 10;
   }
   return count;
}
int main(){

   // two numbers
   long x = 145623;
   long y = 653324;
   printf("The final product is: %ld\n", karatsuba(x, y));
   return 0;
}

输出

The final product is: 95139000852

#include <iostream>
#include <cmath>
using namespace std;
int get_size(long);
long karatsuba(long X, long Y){

   // Base Case
   if (X < 10 && Y < 10)
      return X * Y;

   // determine the size of X and Y
   int size = fmax(get_size(X), get_size(Y));
   if(size < 10)
      return X * Y;

   // rounding up the max length
   size = (size/2) + (size%2);
   long multiplier = pow(10, size);
   long b = X/multiplier;
   long a = X - (b * multiplier);
   long d = Y / multiplier;
   long c = Y - (d * size);
   long u = karatsuba(a, c);
   long z = karatsuba(a + b, c + d);
   long v = karatsuba(b, d);
   return u + ((z - u - v) * multiplier) + (v * (long)(pow(10, 2 * size)));
}
int get_size(long value){
   int count = 0;
   while (value > 0) {
      count++;
      value /= 10;
   }
   return count;
}
int main(){

   // two numbers
   long x = 145623;
   long y = 653324;
   cout << "The final product is: " << karatsuba(x, y) << endl;
   return 0;
}

输出

The final product is: 95139000852

import java.io.*;
public class Main {
   static long karatsuba(long X, long Y) {
      // Base Case
      if (X < 10 && Y < 10)
         return X * Y;
      // determine the size of X and Y
      int size = Math.max(get_size(X), get_size(Y));
      if(size < 10)
         return X * Y;
      // rounding up the max length
      size = (size/2) + (size%2);
      long multiplier = (long)Math.pow(10, size);
      long b = X/multiplier;
      long a = X - (b * multiplier);
      long d = Y / multiplier;
      long c = Y - (d * size);
      long u = karatsuba(a, c);
      long z = karatsuba(a + b, c + d);
      long v = karatsuba(b, d);
      return u + ((z - u - v) * multiplier) + (v * (long)(Math.pow(10, 2 * size)));
   }
   static int get_size(long value) {
      int count = 0;
      while (value > 0) {
         count++;
         value /= 10;
      }
      return count;
   }
   public static void main(String args[]) {
      // two numbers
      long x = 145623;
      long y = 653324;
      System.out.print("The final product is: ");
      long product = karatsuba(x, y);
      System.out.println(product);
   }
}

输出

The final product is: 95139000852

import math
def karatsuba(X, Y):
    if X < 10 and Y < 10:
        return X * Y
    size = max(get_size(X), get_size(Y))
    if size < 10:
        return X * Y
    size = (size // 2) + (size % 2)
    multiplier = 10 ** size
    b = X // multiplier
    a = X - (b * multiplier)
    d = Y // multiplier
    c = Y - (d * size)
    u = karatsuba(a, c)
    z = karatsuba(a + b, c + d)
    v = karatsuba(b, d)
    return u + ((z - u - v) * multiplier) + (v * (10 ** (2 * size)))
def get_size(value):
    count = 0
    while value > 0:
        count += 1
        value //= 10
    return count
x = 145623
y = 653324
print("The final product is: ", end="")
product = karatsuba(x, y)
print(product)

输出

The final product is: 95139000852