设计与分析 - 时间复杂度

---

在本章中，我们将讨论算法的时间复杂度以及影响它的因素。

一般来说，算法的时间复杂度简单地定义为算法实现代码中每条语句所花费的时间。它不是算法的执行时间。该实体可能受到各种因素的影响，例如输入大小、使用的方法和程序。当在尽可能短的时间内产生输出时，算法被认为是最有效的。

计算算法时间复杂度的最常见方法是将算法推导为递归关系。下面让我们进一步探讨一下。

解决递归关系

递推关系是由自身较小的输入定义的方程（或不等式）。这些关系是基于数学归纳法来解决的。在这两个过程中，条件允许将问题分解为更小的部分，这些部分使用较低值的输入执行相同的方程。

这些递推关系可以使用多种方法来解决；他们是 -

• 替代法

• 递归树法

• 迭代法

• 主定理

替代法

替代法是一种试错法；其中我们可能认为可能是该关系的解的值被替换并检查方程是否有效。如果有效，则找到解决方案。否则，将检查另一个值。

程序

使用替换法解决递归问题的步骤是 -

• 基于试错法猜测解决方案的形式

• 使用数学归纳法证明该解决方案对于所有情况都是正确的。

例子

让我们看一个使用替换方法解决递归问题的示例，

T(n) = 2T(n/2) + n

在这里，我们假设方程的时间复杂度为O(nlogn)。所以根据数学归纳现象， T(n/2) 的时间复杂度将为O(n/2logn/2)；将值代入给定方程，我们需要证明 T(n) 必须大于或等于nlogn。

≤ 2n/2Log(n/2) + n
= nLogn – nLog2 + n
= nLogn – n + n
≤ nLogn

递归树法

在递归树方法中，我们绘制递归树，直到程序无法进一步划分为更小的部分。然后我们计算递归树每一层所花费的时间。

程序

• 画出程序的递归树

• 计算每个级别的时间复杂度并将其相加即可得出总时间复杂度。

例子

考虑二分搜索算法并为其构造一个递归树 -

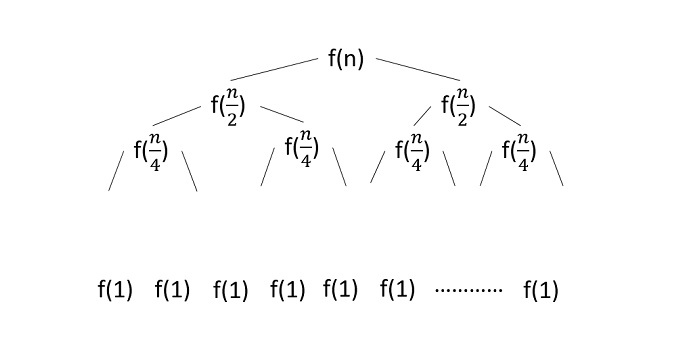
由于该算法遵循分治技术，因此会绘制递归树，直到达到最小输入级别 $\mathrm{T\left ( \frac{n}{2^{k}} \right )}$。

$$\mathrm{T\left ( \frac{n}{2^{k}} \right )=T\left ( 1 \right )}$$

$$\mathrm{n=2^{k}}$$

对方程两边取对数，

$$\mathrm{log\: n=log\: 2^{k}}$$

$$\mathrm{k=log_{2}\:n}$$

因此，二分查找算法的时间复杂度为O(log n)。

大师的方法

马斯特方法或马斯特定理应用于递减或除以递推关系来求出时间复杂度。它使用一组公式来推导算法的时间复杂度。

了解更多关于马斯特定理的信息，请点击这里