设计与分析顶点覆盖

无向图G = (V, E)的顶点覆盖是顶点V ' ⊆ V的子集，这样如果边(u, v)是G的边，则V中的u或V '中的v或两个都。

在给定的无向图中找到最大尺寸的顶点覆盖。这个最优顶点覆盖是 NP 完全问题的优化版本。然而，找到接近最佳的顶点覆盖并不难。

APPROX-VERTEX_COVER (G: Graph) c ← { } E' ← E[G] 
while E' is not empty do 
   Let (u, v) be an arbitrary edge of E' c ← c U {u, v} 
   Remove from E' every edge incident on either u or v 
return c

例子

给定图的边集是 -

{(1,6),(1,2),(1,4),(2,3),(2,4),(6,7),(4,7),(7,8),( 3,8),(3,5),(8,5)}

设置边缘

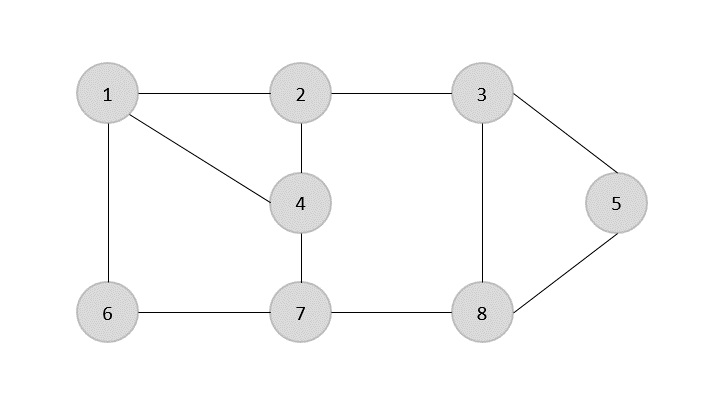
现在，我们首先选择任意边 (1,6)。我们消除所有与顶点 1 或 6 相关的边，并添加边 (1,6) 进行覆盖。

任意边缘

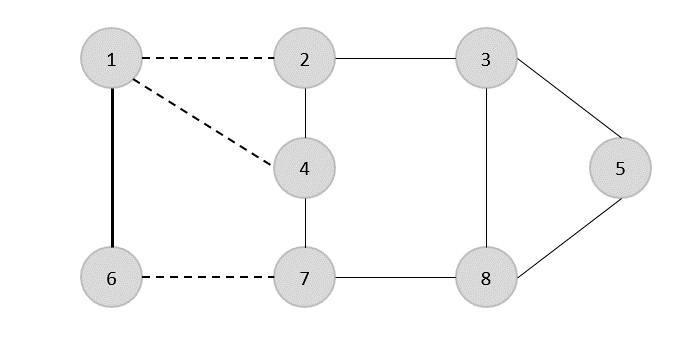
在下一步中，我们随机选择了另一条边 (2,3)

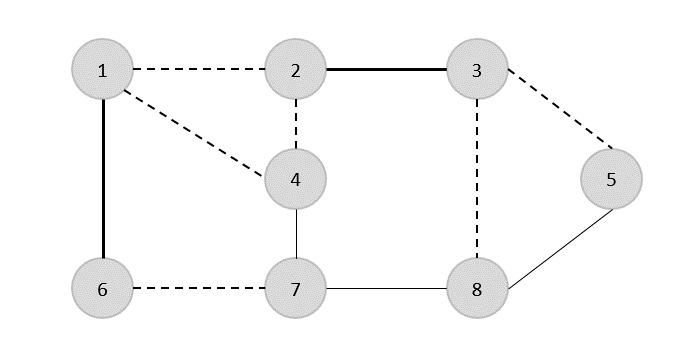
另一个边缘

现在我们选择另一条边 (4,7)。

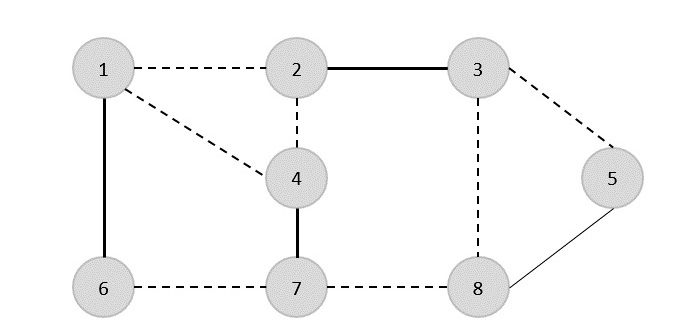
选择另一条边

我们选择另一条边 (8,5)。

边缘

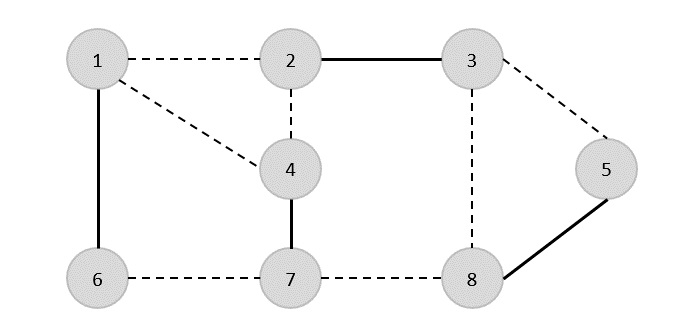
因此，该图的顶点覆盖是{1,2,4,5}。

分析

不难看出，该算法的运行时间为O(V + E)，用邻接表来表示E '。

例子

C C++ Java Python 
#include <stdio.h>
#include <stdbool.h>
#define MAX_VERTICES 100
int graph[MAX_VERTICES][MAX_VERTICES];
bool included[MAX_VERTICES];
// Function to find Vertex Cover using the APPROX-VERTEX_COVER algorithm
void approxVertexCover(int vertices, int edges) {
    bool edgesRemaining[MAX_VERTICES][MAX_VERTICES];
    for (int i = 0; i < vertices; i++) {
        for (int j = 0; j < vertices; j++) {
            edgesRemaining[i][j] = graph[i][j];
        }
    }
    while (edges > 0) {
        int u, v;
        for (int i = 0; i < vertices; i++) {
            for (int j = 0; j < vertices; j++) {
                if (edgesRemaining[i][j]) {
                    u = i;
                    v = j;
                    break;
                }
            }
        }
        included[u] = included[v] = true;
        for (int i = 0; i < vertices; i++) {
            edgesRemaining[u][i] = edgesRemaining[i][u] = false;
            edgesRemaining[v][i] = edgesRemaining[i][v] = false;
        }
        edges--;
    }
}
int main() {
    int vertices = 8;
    int edges = 10;
    int edgesData[10][2] = {{1, 6}, {1, 2}, {1, 4}, {2, 3}, {2, 4},
                            {6, 7}, {4, 7}, {7, 8}, {3, 5}, {8, 5}};
    for (int i = 0; i < edges; i++) {
        int u = edgesData[i][0];
        int v = edgesData[i][1];
        graph[u][v] = graph[v][u] = 1;
    }
    approxVertexCover(vertices, edges);
    printf("Vertex Cover: ");
    for (int i = 1; i <= vertices; i++) {
        if (included[i]) {
            printf("%d ", i);
        }
    }
    printf("\n");
    return 0;
}

输出

Vertex Cover: 1 3 4 5 6 7 

#include <iostream>
#include <vector>
using namespace std;
const int MAX_VERTICES = 100;
vector<vector<int>> graph(MAX_VERTICES, vector<int>(MAX_VERTICES, 0));
vector<bool> included(MAX_VERTICES, false);
// Function to find Vertex Cover using the APPROX-VERTEX_COVER algorithm
void approxVertexCover(int vertices, int edges) {
    vector<vector<bool>> edgesRemaining(vertices, vector<bool>(vertices, false));
    for (int i = 0; i < vertices; i++) {
        for (int j = 0; j < vertices; j++) {
            edgesRemaining[i][j] = graph[i][j];
        }
    }
    while (edges > 0) {
        int u, v;
        for (int i = 0; i < vertices; i++) {
            for (int j = 0; j < vertices; j++) {
                if (edgesRemaining[i][j]) {
                    u = i;
                    v = j;
                    break;
                }
            }
        }
        included[u] = included[v] = true;
        for (int i = 0; i < vertices; i++) {
            edgesRemaining[u][i] = edgesRemaining[i][u] = false;
            edgesRemaining[v][i] = edgesRemaining[i][v] = false;
        }
        edges--;
    }
}
int main() {
    int vertices = 8;
    int edges = 10;
    int edgesData[10][2] = {{1, 6}, {1, 2}, {1, 4}, {2, 3}, {2, 4},
                            {6, 7}, {4, 7}, {7, 8}, {3, 5}, {8, 5}};
    for (int i = 0; i < edges; i++) {
        int u = edgesData[i][0];
        int v = edgesData[i][1];
        graph[u][v] = graph[v][u] = 1;
    }
    approxVertexCover(vertices, edges);
    cout << "Vertex Cover: ";
    for (int i = 1; i <= vertices; i++) {
        if (included[i]) {
            cout << i << " ";
        }
    }
    cout << endl;
    return 0;
}

输出

Vertex Cover: 1 3 4 5 6 7 

import java.util.Arrays;
public class VertexCoverProblem {
    static final int MAX_VERTICES = 100;
    static int[][] graph = new int[MAX_VERTICES][MAX_VERTICES];
    static boolean[] included = new boolean[MAX_VERTICES];
    // Function to find Vertex Cover using the APPROX-VERTEX_COVER algorithm
    static void approxVertexCover(int vertices, int edges) {
        int[][] edgesRemaining = new int[vertices][vertices];
        for (int i = 0; i < vertices; i++) {
            edgesRemaining[i] = Arrays.copyOf(graph[i], vertices);
        }
        while (edges > 0) {
            int u = -1, v = -1;
            for (int i = 0; i < vertices; i++) {
                for (int j = 0; j < vertices; j++) {
                    if (edgesRemaining[i][j] == 1) {
                        u = i;
                        v = j;
                        break;
                    }
                }
            }
            // Check if there are no more edges remaining
            if (u == -1 || v == -1) {
                break;
            }
            included[u] = included[v] = true;
            for (int i = 0; i < vertices; i++) {
                edgesRemaining[u][i] = edgesRemaining[i][u] = 0;
                edgesRemaining[v][i] = edgesRemaining[i][v] = 0;
            }
            edges--;
        }
    }
    public static void main(String[] args) {
        int vertices = 8;
        int edges = 10;
        int[][] edgesData ={{1, 6}, {1, 2}, {1, 4}, {2, 3}, {2, 4},
                            {6, 7}, {4, 7}, {7, 8}, {3, 5}, {8, 5}};
        for (int i = 0; i < edges; i++) {
            int u = edgesData[i][0];
            int v = edgesData[i][1];
            graph[u][v] = graph[v][u] = 1;
        }
        approxVertexCover(vertices, edges);
        System.out.print("Vertex Cover: ");
        for (int i = 1; i <= vertices; i++) {
            if (included[i]) {
                System.out.print(i + " ");
            }
        }
        System.out.println();
    }
}

输出

Vertex Cover: 1 3 4 5 6 7 

MAX_VERTICES = 100
graph = [[0 for _ in range(MAX_VERTICES)] for _ in range(MAX_VERTICES)]
included = [False for _ in range(MAX_VERTICES)]
# Function to find Vertex Cover using the APPROX-VERTEX_COVER algorithm
def approx_vertex_cover(vertices, edges):
    edges_remaining = [row[:] for row in graph]
    while edges > 0:
        for i in range(vertices):
            for j in range(vertices):
                if edges_remaining[i][j]:
                    u = i
                    v = j
                    break
        included[u] = included[v] = True
        for i in range(vertices):
            edges_remaining[u][i] = edges_remaining[i][u] = False
            edges_remaining[v][i] = edges_remaining[i][v] = False
        edges -= 1
if __name__ == "__main__":
    vertices = 8
    edges = 10
    edges_data = [(1, 6), (1, 2), (1, 4), (2, 3), (2, 4),
                  (6, 7), (4, 7), (7, 8), (3, 5), (8, 5)]
    for u, v in edges_data:
        graph[u][v] = graph[v][u] = 1
    approx_vertex_cover(vertices, edges)
    print("Vertex Cover:", end=" ")
    for i in range(1, vertices + 1):
        if included[i]:
            print(i, end=" ")
    print()

输出

Vertex Cover: 1 3 4 5 6 7