设计与分析快速指南

设计与分析简介

算法是解决执行计算、数据处理和自动推理任务的问题的一组操作步骤。算法是一种可以在有限的时间和空间内表达的有效方法。

算法是以非常简单且有效的方式表示特定问题的解决方案的最佳方式。如果我们有针对特定问题的算法，那么我们可以用任何编程语言来实现它，这意味着该算法独立于任何编程语言。

算法设计

算法设计的重要方面包括创建有效的算法，以使用最少的时间和空间以有效的方式解决问题。

为了解决问题，可以采用不同的方法。其中一些方法在时间消耗方面可能是高效的，而其他方法可能是内存效率高的。然而，必须记住，时间消耗和内存使用不能同时优化。如果我们需要算法在更短的时间内运行，我们就必须投资更多的内存，如果我们需要算法在更少的内存下运行，我们就需要更多的时间。

问题发展步骤

解决计算问题涉及以下步骤。

  • 问题定义
  • 模型开发
  • 算法规范
  • 设计算法
  • 检查算法的正确性
  • 算法分析
  • 算法的实现
  • 程序测试
  • 文档

算法特点

算法的主要特点如下 -

  • 算法必须有唯一的名称

  • 算法应该有明确定义的输入和输出集

  • 算法秩序井然，操作明确

  • 算法会在有限的时间内停止。算法不应该无限运行，即算法必须在某个点结束

伪代码

伪代码给出了算法的高级描述，没有与纯文本相关的歧义，而且也不需要知道特定编程语言的语法。

通过使用伪代码将算法表示为一组可以计算的基本操作，可以以更通用的方式估计运行时间。

算法和伪代码之间的区别

算法是具有一些特定特征的形式定义，描述了一个过程，可以由图灵完备的计算机执行以执行特定任务。一般来说，“算法”这个词可以用来描述计算机科学中的任何高级任务。

另一方面，伪代码是对算法的非正式且（通常是基本的）人类可读的描述，留下了许多细粒度的细节。编写伪代码没有风格限制，其唯一目标是用自然语言以更加现实的方式描述算法的高级步骤。

例如，以下是插入排序的算法。

Algorithm: Insertion-Sort 
Input: A list L of integers of length n  
Output: A sorted list L1 containing those integers present in L 
Step 1: Keep a sorted list L1 which starts off empty  
Step 2: Perform Step 3 for each element in the original list L  
Step 3: Insert it into the correct position in the sorted list L1.  
Step 4: Return the sorted list 
Step 5: Stop

这是一个伪代码，描述了如何以更现实的方式描述算法插入排序中的上述高级抽象过程。

for i <- 1 to length(A) 
   x <- A[i] 
   j <- i 
   while j > 0 and A[j-1] > x 
      A[j] <- A[j-1] 
      j <- j - 1 
   A[j] <- x

在本教程中，算法将以伪代码的形式呈现，这在许多方面与 C、C++、Java、Python 和其他编程语言类似。

算法设计与分析

在算法的理论分析中，通常会估计渐进意义上的复杂度，即估计任意大输入的复杂度函数。“算法分析”一词是由唐纳德·高德纳 (Donald Knuth) 创造的。

算法分析是计算复杂性理论的重要组成部分，它为算法解决特定计算问题所需的资源提供理论估计。大多数算法都设计用于处理任意长度的输入。算法分析是确定执行算法所需的时间和空间资源量。

通常，算法的效率或运行时间被表述为输入长度与步骤数（称为时间复杂度）或内存量（称为空间复杂度）相关的函数。

分析的必要性

在本章中，我们将讨论算法分析的必要性以及如何为特定问题选择更好的算法，因为一个计算问题可以通过不同的算法来解决。

通过考虑针对特定问题的算法，我们可以开始开发模式识别，以便可以借助该算法解决类似类型的问题。

尽管这些算法的目标是相同的，但算法通常彼此有很大不同。例如，我们知道可以使用不同的算法对一组数字进行排序。对于同一输入，一种算法执行的比较次数可能会因其他算法而异。因此，这些算法的时间复杂度可能不同。同时，我们需要计算每个算法所需要的内存空间。

算法分析是从所需的时间和大小（实现时存储的内存大小）来分析算法解决问题的能力的过程。然而，算法分析的主要关注点是所需的时间或性能。一般来说，我们执行以下类型的分析 -

  • 最坏情况- 在任何大小为a的实例上采取的最大步数。

  • 最佳情况- 在任何大小为a的实例上采取的最小步数。

  • 平均情况- 在任何大小为a的实例上采取的平均步数。

  • 摊销- 应用于随时间平均大小a的输入的一系列操作。

为了解决问题，我们需要考虑时间和空间复杂度，因为程序可能在内存有限但有足够空间可用的系统上运行，反之亦然。在这种情况下，如果我们比较冒泡排序和归并排序。冒泡排序不需要额外的内存，但合并排序需要额外的空间。虽然冒泡排序的时间复杂度比归并排序更高，但如果程序需要在内存非常有限的环境中运行，我们可能需要应用冒泡排序。

增长率

增长率定义为当输入大小增加时算法运行时间增加的速率。

增长率可分为两种类型：线性增长率和指数增长率。如果算法随着输入大小的增加以线性方式增加，则为线性增长率。而如果算法的运行时间随着输入大小的增加而呈指数增长，那就是指数增长率。

证明算法的正确性

一旦设计了算法来解决问题，算法始终为给定的每个输入返回所需的输出就变得非常重要。因此，需要证明所设计的算法的正确性。这可以使用各种方法来完成 -

反例证明

确定该算法可能不正确的情况并适用。如果反例适用于该算法，则证明其正确性。否则，必须设计另一种算法来解决这个反例。

归纳证明

使用数学归纳法，我们可以通过证明算法对于基本情况输入（例如 1）是正确的，并假设它对于另一个输入 k 是正确的，然后证明它对于 k+1 是正确的，来证明算法对于所有输入都是正确的。

循环不变式证明

找到循环不变式 k，证明基本情况对于算法中的循环不变式成立。然后应用数学归纳法证明算法的其余部分是正确的。

设计和分析方法

为了测量算法的资源消耗，使用了本章讨论的不同策略。

渐近分析

函数f(n)的渐近Behave是指f(n)随着n变大而增长。

我们通常会忽略n的小值，因为我们通常有兴趣估计程序在大输入上的速度有多慢。

一个好的经验法则是，渐近增长率越慢，算法就越好。尽管这并不总是正确的。

例如，线性算法 $f(n) = d * n + k$ 总是渐近优于二次算法 $f(n) = cn^2 + q$。

求解递归方程

递推是一个方程或不等式，它根据较小输入的值来描述函数。递归通常用于分治范式。

让我们将T(n)视为大小为n的问题的运行时间。

如果问题规模足够小，例如n < c，其中c是常数，则直接解决方案需要常数时间，记为θ(1)。如果问题的划分产生了许多大小为$\frac{n}{b}$的子问题。

解决该问题所需的时间为aT(n/b)。如果我们考虑除法所需的时间为D(n)，合并子问题结果所需的时间为C(n)，则递推关系可以表示为 -

$$T(n)=\begin{案例}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \:\:\:\:\theta(1) & 如果\:n\leqslant c\\a T(\frac{n}{b})+D(n)+C(n) & 否则\end{案例}$$

可以使用以下方法解决递归关系 -

  • 替换方法- 在这种方法中，我们猜测一个界限，并使用数学归纳法证明我们的假设是正确的。

  • 递归树方法- 在这种方法中，形成递归树，其中每个节点代表成本。

  • Master's Theorem - 这是查找递归关系复杂性的另一项重要技术。

摊销分析

摊销分析通常用于执行一系列类似操作的某些算法。

  • 摊销分析提供了整个序列的实际成本的界限，而不是单独限制操作序列的成本。

  • 摊销分析不同于平均情况分析；概率不参与摊余分析。摊余分析保证了最坏情况下每个操作的平均性能。

它不仅仅是一个分析工具，更是一种思考设计的方式，因为设计和分析是密切相关的。

聚合法

聚合方法给出了问题的全局视图。在该方法中，如果n次操作总共花费最坏情况时间T(n) 。那么每次操作的摊余成本就是T(n)/n。尽管不同的操作可能需要不同的时间，但在该方法中忽略了不同的成本。

核算方法

在此方法中，根据不同的操作的实际成本分配不同的费用。如果操作的摊余成本超过其实际成本，则差额将作为贷项分配给对象。该信用额有助于支付摊余成本低于实际成本的后续运营费用。

如果第 i次操作的实际成本和摊余成本分别为 $c_{i}$ 和 $\hat{c_{l}}$，则

$$\displaystyle\sum\limits_{i=1}^n \hat{c_{l}}\geqslant\displaystyle\sum\limits_{i=1}^n c_{i}$$

电位法

该方法将预付费工作视为势能，而不是将预付费工作视为信用。这些能量可以被释放来支付未来的运营费用。

如果我们从初始数据结构D 0开始执行n次操作。让我们考虑，c i为实际成本，D i为第 i次操作的数据结构。势函数 Ф 映射到实数 Ф( Di ) ，即Di的相关势。摊余成本 $\hat{c_{l}}$ 可以定义为

$$\hat{c_{l}}=c_{i}+\Phi (D_{i})-\Phi (D_{i-1})$$

因此，总摊余成本为

$$\displaystyle\sum\limits_{i=1}^n \hat{c_{l}}=\displaystyle\sum\limits_{i=1}^n (c_{i}+\Phi (D_{i}) )-\Phi (D_{i-1}))=\displaystyle\sum\limits_{i=1}^n c_{i}+\Phi (D_{n})-\Phi (D_{0})$ $

动态表

如果为表分配的空间不够，我们必须将表复制到更大尺寸的表中。同样，如果从表中删除大量成员，最好重新分配较小大小的表。

使用摊余分析，我们可以证明插入和删除的摊余成本是恒定的，动态表中的未使用空间永远不会超过总空间的恒定比例。

在本教程的下一章中，我们将简要讨论渐近符号。

渐近符号和 Apriori 分析

在算法设计中，算法的复杂度分析是一个重要的方面。算法复杂性主要与它的性能、运行速度有多快或多慢有关。

算法的复杂度以处理数据所需的内存量和处理时间来描述算法的效率。

算法的复杂度从时间和空间两个角度来分析。

时间复杂度

它是一个函数，根据输入的大小描述运行算法所需的时间。“时间”可以指执行的内存访问次数、整数之间的比较次数、执行某些内部循环的次数，或与算法将花费的实时量相关的一些其他自然单位。

空间复杂度

它是一个函数，根据算法输入的大小来描述算法占用的内存量。我们经常谈到需要“额外”内存，而不是计算存储输入本身所需的内存。同样，我们使用自然（但固定长度）单位来衡量这一点。

空间复杂性有时会被忽略，因为所使用的空间很小和/或明显，但有时它变得与时间一样重要。

渐近符号

算法的执行时间取决于指令集、处理器速度、磁盘 I/O 速度等。因此，我们渐近地估计算法的效率。

算法的时间函数由T(n)表示，其中n是输入大小。

不同类型的渐近符号用于表示算法的复杂性。以下渐近符号用于计算算法的运行时间复杂度。

  • O – 大哦

  • Ω - 大欧米茄

  • θ - 大θ

  • o - 小哦

  • ω - 小欧米茄

O：渐近上限

“O”（Big Oh）是最常用的符号。函数f(n)可以表示为g(n)的阶数，即O(g(n))，如果存在正整数 n 的值n 0和正常数c使得 -

$f(n)\leqslant cg(n)$ 在所有情况下 $n > n_{0}$

因此，函数g(n)是函数f(n)的上限，因为g(n) 的增长速度比f(n)快。

例子

让我们考虑一个给定的函数，$f(n) = 4.n^3 + 10.n^2 + 5.n + 1$

考虑$g(n) = n^3$，

$f(n)\leqslant 5.g(n)$ 对于 $n > 2$ 的所有值

因此， f(n)的复杂度可以表示为$O(g(n))$，即$O(n^3)$

Ω：渐近下界

当对于所有足够大的n值存在 $f(n)\geqslant cg(n)$ 的常数c时，我们说 $f(n) = \Omega (g(n))$ 。这里n是一个正整数。这意味着函数g是函数f的下界；在 n达到某个值后， f永远不会低于g。

例子

让我们考虑一个给定的函数，$f(n) = 4.n^3 + 10.n^2 + 5.n + 1$。

考虑 $g(n) = n^3$，对于 $n > 0$ 的所有值，$f(n)\geqslant 4.g(n)$。

因此， f(n)的复杂度可以表示为$\Omega (g(n))$，即$\Omega (n^3)$

θ：渐近紧界

当存在常数c 1和c 2 $c_{1}.g(n) \leqslant f(n) \leqslant c_{2} 时，我们说 $f(n) = \theta(g(n))$ .g(n)$ 对于所有足够大的n值。这里n是一个正整数。

这意味着函数g是函数f的紧界。

例子

让我们考虑一个给定的函数，$f(n) = 4.n^3 + 10.n^2 + 5.n + 1$

考虑 $g(n) = n^3$，对于n的所有大值， $4.g(n) \leqslant f(n) \leqslant 5.g(n)$ 。

因此， f(n)的复杂度可以表示为$\theta (g(n))$，即$\theta (n^3)$。

O - 表示法

O 表示法提供的渐近上限可能是渐近紧的，也可能不是渐近紧的。界限 $2.n^2 = O(n^2)$ 是渐近紧的，但界限 $2.n = O(n^2)$ 不是。

我们使用o 符号来表示非渐近紧的上限。

我们正式将o(g(n))（n 的 g 的小 oh）定义为对于任何正常数 $c > 0$ 的集合f(n) = o(g(n))，并且存在一个值 $n_ {0} > 0$，使得 $0 \leqslant f(n) \leqslant cg(n)$。

直观上，在o 表示法中，当n接近无穷大时，函数f(n)相对于g(n)变得微不足道；那是，

$$\lim_{n \rightarrow \infty}\left(\frac{f(n)}{g(n)}\right) = 0$$

例子

让我们考虑相同的函数，$f(n) = 4.n^3 + 10.n^2 + 5.n + 1$

考虑 $g(n) = n^{4}$，

$$\lim_{n \rightarrow \infty}\left(\frac{4.n^3 + 10.n^2 + 5.n + 1}{n^4}\right) = 0$$

因此， f(n)的复杂度可以表示为$o(g(n))$，即$o(n^4)$。

ω – 符号

我们使用ω 表示法来表示非渐近紧的下界。然而，正式地，我们将ω(g(n))（n 的 g 的小欧米伽）定义为对于任何正常数C > 0的集合f(n) = ω(g(n))，并且存在一个值 $ n_{0} > 0$，使得 $0 \leqslant cg(n) < f(n)$。

例如，$\frac{n^2}{2} = \omega (n)$，但 $\frac{n^2}{2} \neq \omega (n^2)$。关系 $f(n) = omega (g(n))$ 意味着存在以下极限

$$\lim_{n \rightarrow \infty}\left(\frac{f(n)}{g(n)}\right) = \infty$$

也就是说，当n接近无穷大时， f(n)相对于g(n)变得任意大。

例子

让我们考虑相同的函数，$f(n) = 4.n^3 + 10.n^2 + 5.n + 1$

考虑$g(n) = n^2$，

$$\lim_{n \rightarrow \infty}\left(\frac{4.n^3 + 10.n^2 + 5.n + 1}{n^2}\right) = \infty$$

因此， f(n)的复杂度可以表示为$o(g(n))$，即$\omega(n^2)$。

Apriori 和 Apostiari 分析

Apriori 分析是指在特定系统上运行之前执行分析。该分析是使用某种理论模型定义函数的阶段。因此，我们通过仅查看算法来确定算法的时间和空间复杂度，而不是在具有不同内存、处理器和编译器的特定系统上运行它。

Apostiari 算法分析意味着我们只有在系统上运行算法后才对其进行分析。它直接取决于系统，并且随着系统的不同而变化。

在行业中，我们无法进行 Apostiari 分析，因为该软件通常是为匿名用户制作的，该用户在与行业中存在的系统不同的系统上运行该软件。

在 Apriori 中，这就是我们使用渐近符号来确定时间和空间复杂度随计算机的变化而变化的原因；然而，它们渐近是相同的。

设计与分析 - 时间复杂度

在本章中，我们将讨论算法的时间复杂度以及影响它的因素。

一般来说，算法的时间复杂度简单地定义为算法实现代码中每条语句所花费的时间。它不是算法的执行时间。该实体可能受到各种因素的影响，例如输入大小、使用的方法和程序。当在尽可能短的时间内产生输出时，算法被认为是最有效的。

计算算法时间复杂度的最常见方法是将算法推导为递归关系。下面让我们进一步探讨一下。

解决递归关系

递推关系是由自身较小的输入定义的方程（或不等式）。这些关系是基于数学归纳法来解决的。在这两个过程中，条件允许将问题分解为更小的部分，这些部分使用较低值的输入执行相同的方程。

这些递推关系可以使用多种方法来解决；他们是 -

  • 替代法

  • 递归树法

  • 迭代法

  • 主定理

替代法

替代法是一种试错法；其中我们可能认为可能是该关系的解的值被替换并检查方程是否有效。如果有效，则找到解决方案。否则，将检查另一个值。

程序

使用替换法解决递归问题的步骤是 -

  • 基于试错法猜测解决方案的形式

  • 使用数学归纳法证明该解决方案对于所有情况都是正确的。

例子

让我们看一个使用替换方法解决递归问题的示例，

T(n) = 2T(n/2) + n

在这里，我们假设方程的时间复杂度为O(nlogn)。所以根据数学归纳现象， T(n/2) 的时间复杂度将为O(n/2logn/2)；将值代入给定方程，我们需要证明 T(n) 必须大于或等于nlogn。

≤ 2n/2Log(n/2) + n
= nLogn – nLog2 + n
= nLogn – n + n
≤ nLogn

递归树法

在递归树方法中，我们绘制递归树，直到程序无法进一步划分为更小的部分。然后我们计算递归树每一层所花费的时间。

程序

  • 画出程序的递归树

  • 计算每个级别的时间复杂度并将其相加即可得出总时间复杂度。

例子

考虑二分搜索算法并为其构造一个递归树 -

递归树

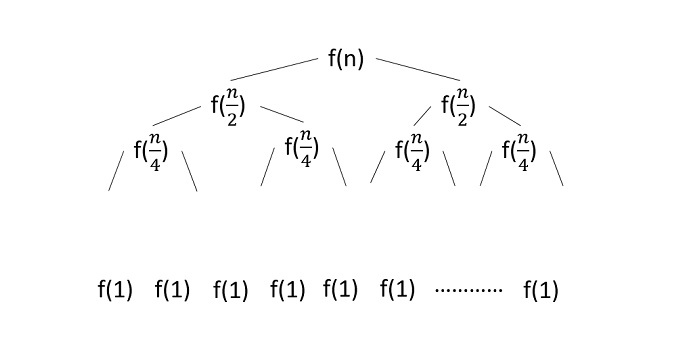
由于该算法遵循分治技术，因此会绘制递归树，直到达到最小输入级别 $\mathrm{T\left ( \frac{n}{2^{k}} \right )}$。

$$\mathrm{T\left ( \frac{n}{2^{k}} \right )=T\left ( 1 \right )}$$

$$\mathrm{n=2^{k}}$$

对方程两边取对数，

$$\mathrm{log\: n=log\: 2^{k}}$$

$$\mathrm{k=log_{2}\:n}$$

因此，二分查找算法的时间复杂度为O(log n)。

大师的方法

马斯特方法或马斯特定理应用于递减或除以递推关系来求出时间复杂度。它使用一组公式来推导算法的时间复杂度。

了解更多关于马斯特定理的信息，请点击这里

设计与分析 - 马斯特定理

马斯特定理是用于计算算法时间复杂度的众多方法之一。在分析中，通过计算时间复杂度来找出算法的最佳逻辑。马斯特定理应用于递推关系。

但在我们深入研究主定理之前，让我们首先回顾一下什么是递推关系 -

递归关系是定义元素序列的方程，其中一项是其前一项的函数。在算法分析中，递归关系通常是在算法中存在循环时形成的。

问题陈述

马斯特定理只能应用于递减和除法循环函数。如果关系不是递减或除除，则不能应用马斯特定理。

函数除法的马斯特定理

考虑类型的关系 -

T(n) = aT(n/b) + f(n)

其中，a >= 1且b > 1，

n - 问题的大小

a - 递归中的子问题数

n/b - 基于所有子问题大小相同的假设的子问题的大小。

f(n) - 表示递归之外完成的工作成本 -> θ(nk logn p) ，其中 k >= 0 并且 p 是实数；

如果递推关系是上面给定的形式，那么主定理中存在三种情况来确定渐近符号 -

  • 如果 a > b k，则 T(n)= θ (n logb a ) [ log b a = log a / log b。]

  • 如果 a = b k

    • 如果 p > -1，则 T(n) = θ (n logb a log p+1 n)

    • 如果 p = -1，则 T(n) = θ (n logb a log log n)

    • 如果 p < -1，则 T(n) = θ (n logb a )

  • 如果 a < b k，

    • 如果 p >= 0，则 T(n) = θ (n k log p n)。

    • 如果 p < 0，则 T(n) = θ (n k )

马斯特递减函数定理

考虑类型的关系 -

T(n) = aT(n-b) + f(n)
where, a >= 1 and b > 1, f(n) is asymptotically positive

这里，

n - 问题的大小

a - 递归中的子问题数

nb - 基于所有子问题大小相同的假设的子问题的大小。

f(n) - 表示在递归之外完成的工作成本 -> θ(n k )，其中 k >= 0。

如果递推关系是上面给定的形式，那么主定理中存在三种情况来确定渐近符号 -

  • 如果 a = 1，则 T(n) = O (n k+1 )

  • 如果 a > 1，则 T(n) = O (a n/b * n k )

  • 如果 a < 1，则 T(n) = O (n k )

例子

应用主定理除以递推关系的几个例子-

实施例1

考虑递推关系，如 T(n) = 8T(n/2) + n 2

In this problem, a = 8, b = 2 and f(n) = Θ(nk logn p) = n2, giving us k = 2 and p = 0.
a = 8 > bk = 22 = 4,
Hence, case 1 must be applied for this equation.
To calculate, T(n) = Θ (nlogb a )
   = nlog28
   = n( log 8 / log 2 )
   = n3
Therefore, T(n) = Θ(n3) is the tight bound for this equation.

实施例2

考虑递推关系，如 T(n) = 4T(n/2) + n 2

In this problem, a = 4, b = 2 and f(n) = Θ(nk logn p) = n2, giving us k = 2 and p = 0.
a = 4 = bk = 22 = 4, p > -1
Hence, case 2(i) must be applied for this equation.
To calculate, T(n) = Θ (nlogb a logp+1 n)
   = nlog24 log0+1n
   = n2logn
Therefore, T(n) = Θ(n2logn) is the tight bound for this equation.

实施例3

考虑递推关系，如 T(n) = 2T(n/2) + n/log n

In this problem, a = 2, b = 2 and f(n) = Θ(nk logn p) = n/log n, giving us k = 1 and p = -1.
a = 2 = bk = 21 = 2, p = -1
Hence, case 2(ii) must be applied for this equation.
To calculate, T(n) = Θ (n logb a log log n)
   = nlog44 log logn
   = n.log(logn)
Therefore, T(n) = Θ(n.log(logn)) is the tight bound for this equation.

实施例4

考虑递推关系，如 T(n) = 16T(n/4) + n 2 /log 2 n

In this problem, a = 16, b = 4 and f(n) = Θ(nk logn p) = n2/log2n, giving us k = 2 and p = -2.
a = 16 = bk = 42 = 16, p < -1
Hence, case 2(iii) must be applied for this equation.
To calculate, T(n) = Θ (n logb a)
   = nlog416
   = n2
Therefore, T(n) = Θ(n2) is the tight bound for this equation.

实施例5

考虑递推关系，如 T(n) = 2T(n/2) + n 2

In this problem, a = 2, b = 2 and f(n) = Θ(nk logn p) = n2, giving us k = 2 and p = 0.
a = 2 < bk = 22 = 4, p = 0
Hence, case 3(i) must be applied for this equation.
To calculate, T(n) = Θ (nk logp n)
   = n2 log0n
   = n2
Therefore, T(n) = Θ(n2) is the tight bound for this equation.

实施例6

考虑递推关系，如 T(n) = 2T(n/2) + n 3 /log n

In this problem, a = 2, b = 2 and f(n) = Θ(nk logn p) = n3/log n, giving us k = 3 and p = -1.
a = 2 < bk = 23 = 8, p < 0
Hence, case 3(ii) must be applied for this equation.
To calculate, T(n) = Θ (nk)
   = n3
   = n3
Therefore, T(n) = Θ(n3) is the tight bound for this equation.

在减少递推关系中应用大师定理的几个例子-

实施例1

考虑递推关系，如 T(n) = T(n-1) + n 2

In this problem, a = 1, b = 1 and f(n) = O(nk) = n2, giving us k = 2.
Since a = 1, case 1 must be applied for this equation.
To calculate, T(n) = O(nk+1)
   = n2+1
   = n3
Therefore, T(n) = O(n3) is the tight bound for this equation.

实施例2

考虑递推关系，如 T(n) = 2T(n-1) + n

In this problem, a = 2, b = 1 and f(n) = O(nk) = n, giving us k = 1.
Since a > 1, case 2 must be applied for this equation.
To calculate, T(n) = O(an/b * nk)
   = O(2n/1 * n1)
   = O(n2n)
Therefore, T(n) = O(n2n) is the tight bound for this equation.

实施例3

考虑递推关系，如 T(n) = n 4

In this problem, a = 0 and f(n) = O(nk) = n4, giving us k = 4
Since a < 1, case 3 must be applied for this equation.
To calculate, T(n) = O(nk)
   = O(n4)
   = O(n4)
Therefore, T(n) = O(n4) is the tight bound for this equation.

设计和分析空间复杂性

在本章中，我们将讨论计算问题的复杂性与算法所需空间量的关系。

空间复杂度具有时间复杂度的许多特征，并且可以作为根据计算难度对问题进行分类的进一步方法。

什么是空间复杂度？

空间复杂度是一个函数，描述算法根据算法的输入量占用的内存（空间）量。

我们经常谈论需要额外的内存，而不是计算存储输入本身所需的内存。同样，我们使用自然（但固定长度）单位来衡量这一点。

我们可以使用字节，但使用起来更容易，比如使用的整数数量、固定大小结构的数量等。

最后，我们提出的函数将独立于表示该单元所需的实际字节数。

空间复杂度有时会被忽略，因为所使用的空间很小和/或明显，但有时它变得与时间复杂度一样重要

定义

令M为确定性图灵机 (TM)，在所有输入上都会停止。M的空间复杂度是函数 $f \colon N \rightarrow N$，其中f(n)是磁带的最大单元数，M扫描长度为M的任何输入。如果M的空间复杂度为f(n)，我们可以说M在空间f(n)中运行。

我们使用渐近符号来估计图灵机的空间复杂度。

设 $f \colon N \rightarrow R^+$ 是一个函数。空间复杂度类可以定义如下 -

空间 = {L | L 是由 O(f(n)) 空间确定性 TM 决定的语言}

空间 = {L | L 是由 O(f(n)) 空间非确定性 TM 决定的语言}

PSPACE是在确定性图灵机上的多项式空间中可判定的一类语言。

换句话说，PSPACE = U k SPACE (n k )

萨维奇定理

与空间复杂性相关的最早的定理之一是萨维奇定理。根据该定理，确定性机器可以使用少量空间来模拟非确定性机器。

对于时间复杂度来说，这样的模拟似乎需要时间呈指数增长。对于空间复杂度，该定理表明任何使用f(n)空间的非确定性图灵机都可以转换为使用f 2 (n)空间的确定性 TM。

因此，萨维奇定理指出，对于任何函数，$f \colon N \rightarrow R^+$，其中 $f(n) \geqslant n$

NSPACE(f(n)) ⊆ 空间(f(n))

复杂性类别之间的关系

下图描述了不同复杂性类别之间的关系。

关系

到目前为止，我们还没有在本教程中讨论 P 类和 NP 类。这些将在稍后讨论。

设计与分析 - 分而治之

使用分而治之的方法，将手头的问题分成更小的子问题，然后独立解决每个问题。当我们不断地将子问题划分为更小的子问题时，我们最终可能会达到无法再划分的阶段。这些最小的可能子问题是使用原始解决方案来解决的，因为它需要更少的计算时间。最后将所有子问题的解进行合并，得到原问题的解。

分而治之的方法

从广义上讲，我们可以通过三步过程来理解分而治之的方法。

划分/打破

此步骤涉及将问题分解为更小的子问题。子问题应该代表原始问题的一部分。这一步一般采用递归的方式来划分问题，直到没有子问题可进一步整除为止。在此阶段，子问题的大小变得Atomics，但仍然代表实际问题的某些部分。

征服/解决

这一步接收到许多需要解决的较小的子问题。一般来说，在这个级别上，问题被认为是自行“解决”的。

合并/组合

当较小的子问题得到解决后，此阶段会递归地组合它们，直到它们形成原始问题的解决方案。这种算法方法以递归方式工作，并且征服和合并步骤的工作方式非常接近，以至于它们看起来像是一个整体。

分而治之的方法的优点和缺点

分而治之的方法支持并行性，因为子问题是独立的。因此，使用这种技术设计的算法可以在多处理器系统上或同时在不同的机器上运行。

在这种方法中，大多数算法都是使用递归设计的，因此内存管理非常高。对于递归函数，使用堆栈，其中需要存储函数状态。

分而治之的例子

以下计算机算法基于分而治之的编程方法 -

  • 归并排序

  • 快速排序

  • 二分查找

  • 施特拉森矩阵乘法

  • 最接近的对（点）

  • 唐叶

解决任何计算机问题都有多种方法，但提到的方法是分而治之的一个很好的例子。

设计与分析最大最小问题

让我们考虑一个可以通过分而治之技术解决的简单问题。

问题陈述

算法分析中的最大最小问题是寻找数组中的最大值和最小值。

解决方案

要查找给定大小为n的数组Numbers[]中的最大和最小数字，可以使用以下算法。首先我们介绍朴素方法，然后我们将介绍分而治之的方法。

朴素方法

朴素方法是解决任何问题的基本方法。在这种方法中，可以分别找到最大和最小数。要找到最大和最小数字，可以使用以下简单的算法。

Algorithm: Max-Min-Element (numbers[]) 
max := numbers[1] 
min := numbers[1] 

for i = 2 to n do 
   if numbers[i] > max then  
      max := numbers[i] 
   if numbers[i] < min then  
      min := numbers[i] 
return (max, min)

分析

Naive 方法中的比较次数为2n - 2。

使用分而治之的方法可以减少比较的次数。下面是技术。

分而治之的方法

在这种方法中，数组被分为两半。然后使用递归方法找到每一半中的最大和最小数。然后，返回每半部分的两个最大值中的最大值和每半部分中的两个最小值中的最小值。

在此给定问题中，数组中的元素数量为 $y - x + 1$，其中y大于或等于x。

$\mathbf{\mathit{Max - Min(x, y)}}$ 将返回数组 $\mathbf{\mathit{numbers[x...y]}}$ 的最大值和最小值。

Algorithm: Max - Min(x, y) 
if y – x ≤ 1 then  
   return (max(numbers[x], numbers[y]), min((numbers[x], numbers[y])) 
else 
   (max1, min1):= maxmin(x, ⌊((x + y)/2)⌋) 
   (max2, min2):= maxmin(⌊((x + y)/2) + 1)⌋,y) 
return (max(max1, max2), min(min1, min2))

分析

令T(n)为 $\mathbf{\mathit{Max - Min(x, y)}}$ 进行的比较次数，其中元素数量 $n = y - x + 1$。

如果T(n)代表数字，那么递推关系可以表示为

$$T(n) = \begin{cases}T\left(\lfloor\frac{n}{2}\rfloor\right)+T\left(\lceil\frac{n}{2}\rceil\right )+2 & 对于\: n>2\\1 & 对于\:n = 2 \\0 & 对于\:n = 1\end{cases}$$

让我们假设n是2的幂的形式。因此，n = 2 k，其中k是递归树的高度。

所以，

$$T(n) = 2.T (\frac{n}{2}) + 2 = 2.\left(\begin{array}{c}2.T(\frac{n}{4}) + 2\end{数组}\right) + 2 ..... = \frac{3n}{2} - 2$$

与 Naïve 方法相比，分治法中的比较次数较少。然而，使用渐近符号，这两种方法都由O(n)表示。

设计与分析快速排序

快速排序是一种高效的排序算法，基于将数据数组划分为更小的数组。一个大数组被划分为两个数组，其中一个数组保存小于指定值（例如枢轴）的值，根据该值进行分区，另一个数组保存大于枢轴值的值。

快速排序对数组进行分区，然后递归调用自身两次以对两个结果子数组进行排序。该算法对于大型数据集非常有效，因为其平均复杂度和最坏情况复杂度分别为 O(n2)。

快速排序中的分区

以下动画演示解释了如何查找数组中的主元值。

快速排序

枢轴值将列表分为两部分。递归地，我们找到每个子列表的主元，直到所有列表仅包含一个元素。

快速排序枢轴算法

基于我们对快速排序中分区的理解，我们现在尝试为其编写一个算法，如下所示。

步骤 1 - 选择具有枢轴的最高索引值

步骤 2 - 将两个变量指向列表的左侧和右侧（不包括枢轴）

步骤 3 - 左点指向低索引

步骤 4 - 向右指向高点

步骤 5 - 当左侧的值小于枢轴向右移动时

步骤 6 - 当右侧的值大于枢轴向左移动时

步骤 7 - 如果步骤 5 和步骤 6 都不匹配，则左右交换

步骤 8 - 如果左≥右，则它们相遇的点是新的枢轴

快速排序枢轴伪代码

上述算法的伪代码可以导出为 -

function partitionFunc(left, right, pivot)
   leftPointer = left
   rightPointer = right - 1

   while True do
      while A[++leftPointer] < pivot do
      //do-nothing            
      end while
		
      while rightPointer > 0 && A[--rightPointer] > pivot do
         //do-nothing         
      end while
		
      if leftPointer >= rightPointer
         break
      else                
         swap leftPointer,rightPointer
      end if
   end while 
	
   swap leftPointer,right
   return leftPointer
end function

快速排序算法

递归地使用枢轴算法，我们最终得到更小的可能分区。然后处理每个分区以进行快速排序。我们定义快速排序的递归算法如下 -

步骤 1 - 制作最右边的索引值枢轴

步骤 2 - 使用主元值对数组进行分区

步骤 3 - 递归快速排序左分区

步骤 4 - 递归快速排序右分区

快速排序伪代码

为了更深入地了解它，让我们看看快速排序算法的伪代码 -

procedure quickSort(left, right)
   if right-left <= 0
      return
   else     
      pivot = A[right]
      partition = partitionFunc(left, right, pivot)
      quickSort(left,partition-1)
      quickSort(partition+1,right)    
   end if		
end procedure

分析

快速排序算法最坏情况的复杂度是O(n 2 )。然而，使用这种技术，在一般情况下，我们通常会在O(n log n)时间内获得输出。

执行

以下是快速排序算法在不同语言中的实现 -

C C++ Java Python 
#include <stdio.h>
#include <stdbool.h>
#define MAX 7

int intArray[MAX] = {
   4,
   6,
   3,
   2,
   1,
   9,
   7
};

void printline(int count) {
   int i;

   for (i = 0; i < count - 1; i++) {
      printf("=");
   }

   printf("=\n");
}

void display() {
   int i;
   printf("[");

   // navigate through all items 
   for (i = 0; i < MAX; i++) {
      printf("%d ", intArray[i]);
   }

   printf("]\n");
}

void swap(int num1, int num2) {
   int temp = intArray[num1];
   intArray[num1] = intArray[num2];
   intArray[num2] = temp;
}

int partition(int left, int right, int pivot) {
   int leftPointer = left - 1;
   int rightPointer = right;

   while (true) {
      while (intArray[++leftPointer] < pivot) {
         //do nothing
      }

      while (rightPointer > 0 && intArray[--rightPointer] > pivot) {
         //do nothing
      }

      if (leftPointer >= rightPointer) {
         break;
      } else {
         printf(" item swapped :%d,%d\n", intArray[leftPointer], intArray[rightPointer]);
         swap(leftPointer, rightPointer);
      }
   }

   printf(" pivot swapped :%d,%d\n", intArray[leftPointer], intArray[right]);
   swap(leftPointer, right);
   printf("Updated Array: ");
   display();
   return leftPointer;
}

void quickSort(int left, int right) {
   if (right - left <= 0) {
      return;
   } else {
      int pivot = intArray[right];
      int partitionPoint = partition(left, right, pivot);
      quickSort(left, partitionPoint - 1);
      quickSort(partitionPoint + 1, right);
   }
}

int main() {
   printf("Input Array: ");
   display();
   printline(50);
   quickSort(0, MAX - 1);
   printf("Output Array: ");
   display();
   printline(50);
}

输出

Input Array: [4 6 3 2 1 9 7 ]
==================================================
 pivot swapped :9,7
Updated Array: [4 6 3 2 1 7 9 ]
 pivot swapped :4,1
Updated Array: [1 6 3 2 4 7 9 ]
 item swapped :6,2
 pivot swapped :6,4
Updated Array: [1 2 3 4 6 7 9 ]
 pivot swapped :3,3
Updated Array: [1 2 3 4 6 7 9 ]
Output Array: [1 2 3 4 6 7 9 ]
==================================================

#include <iostream>
using namespace std;

#define MAX 7

int intArray[MAX] = {4,6,3,2,1,9,7};

void display() {
   int i;
   cout << "[";
	
   // navigate through all items 
   for(i = 0;i < MAX;i++) {
      cout << intArray[i] << " ";
   }
	
   cout << "]\n";
}

void swap(int num1, int num2) {
   int temp = intArray[num1];
   intArray[num1] = intArray[num2];
   intArray[num2] = temp;
}

int partition(int left, int right, int pivot) {
   int leftPointer = left -1;
   int rightPointer = right;

   while(true) {
      while(intArray[++leftPointer] < pivot) {
         //do nothing
      }
		
      while(rightPointer > 0 && intArray[--rightPointer] > pivot) {
         //do nothing
      }

      if(leftPointer >= rightPointer) {
            break;
      } else {
            cout << "item swapped : " << intArray[leftPointer] << "," << intArray[rightPointer] << endl;
         swap(leftPointer, rightPointer);
      }
   }
	
   cout << "\npivot swapped : " << intArray[leftPointer] << "," << intArray[right] << endl;
   swap(leftPointer,right);
   cout << "Updated Array: "; 
   display();
   return leftPointer;
}

void quickSort(int left, int right) {
   if(right-left <= 0) {
      return;   
   } else {
      int pivot = intArray[right];
      int partitionPoint = partition(left, right, pivot);
      quickSort(left, partitionPoint - 1);
      quickSort(partitionPoint + 1,right);
   }        
}

int main() {
   cout << "Input Array: ";
   display();
   quickSort(0, MAX-1);
   cout << "\nOutput Array: ";
   display();
}

输出

Input Array: [4 6 3 2 1 9 7 ]

pivot swapped : 9,7
Updated Array: [4 6 3 2 1 7 9 ]

pivot swapped : 4,1
Updated Array: [1 6 3 2 4 7 9 ]
item swapped : 6,2

pivot swapped : 6,4
Updated Array: [1 2 3 4 6 7 9 ]

pivot swapped : 3,3
Updated Array: [1 2 3 4 6 7 9 ]

Output Array: [1 2 3 4 6 7 9 ]

import java.util.Arrays;

public class QuickSortExample {
   int[] intArray = {
      4,
      6,
      3,
      2,
      1,
      9,
      7
   };

   void swap(int num1, int num2) {
      int temp = intArray[num1];
      intArray[num1] = intArray[num2];
      intArray[num2] = temp;
   }
   int partition(int left, int right, int pivot) {
      int leftPointer = left - 1;
      int rightPointer = right;

      while (true) {
         while (intArray[++leftPointer] < pivot) {
            // do nothing
         }
         while (rightPointer > 0 && intArray[--rightPointer] > pivot) {
            // do nothing
         }

         if (leftPointer >= rightPointer) {
            break;
         } else {
            swap(leftPointer, rightPointer);
         }
      }
      swap(leftPointer, right);

      // System.out.println("Updated Array: "); 
      return leftPointer;
   }
   void quickSort(int left, int right) {
      if (right - left <= 0) {
         return;
      } else {
         int pivot = intArray[right];
         int partitionPoint = partition(left, right, pivot);
         quickSort(left, partitionPoint - 1);
         quickSort(partitionPoint + 1, right);
      }
   }
   public static void main(String[] args) {
      QuickSortExample sort = new QuickSortExample();
      int max = sort.intArray.length;
      System.out.println("Contents of the array :");
      System.out.println(Arrays.toString(sort.intArray));

      sort.quickSort(0, max - 1);
      System.out.println("Contents of the array after sorting :");
      System.out.println(Arrays.toString(sort.intArray));
   }
}

输出

Contents of the array :
[4, 6, 3, 2, 1, 9, 7]
Contents of the array after sorting :
[1, 2, 3, 4, 6, 7, 9]

def partition(arr, low, high):
   i = low - 1
   pivot = arr[high]  # pivot element
   for j in range(low, high):
      if arr[j] <= pivot:
         # increment
         i = i + 1
         arr[i], arr[j] = arr[j], arr[i]
   arr[i + 1], arr[high] = arr[high], arr[i + 1]
   return i + 1

def quickSort(arr, low, high):
   if low < high:
      pi = partition(arr, low, high)
      quickSort(arr, low, pi - 1)
      quickSort(arr, pi + 1, high)

arr = [2, 5, 3, 8, 6, 5, 4, 7]
n = len(arr)
quickSort(arr, 0, n - 1)
print("Sorted array is:")
for i in range(n):
   print(arr[i], end=" ")

输出

Sorted array is:
2 3 4 5 5 6 7 8

设计与分析 - 二分搜索

二分搜索法是一种遵循分而治之技术的搜索算法。这是基于有序搜索的思想，其中算法将排序列表分为两半并执行搜索。如果要查找的键值低于排序列表的中点值，则在左半部分查找；否则它会搜索右半部分。如果数组未排序，则使用线性搜索来确定位置。

二分查找算法

在此算法中，我们要查找元素 x 是否属于存储在数组Numbers [] 中的一组数字。其中l和r表示要执行搜索操作的子数组的左索引和右索引。

Algorithm: Binary-Search(numbers[], x, l, r)
   if l = r then
      return l
   else
      m := $\lfloor (l + r) / 2\rfloor$
   if x ≤ numbers[m] then
      return Binary-Search(numbers[], x, l, m)
   else
      return Binary-Search(numbers[], x, m+1, r)

例子

在此示例中，我们将搜索元素 63。

二分查找

分析

线性搜索的运行时间为O(n)。而二分查找则在O(log n)时间内产生结果。

令T(n)为n 个元素的数组中最坏情况下的比较次数。

因此，

$$T\left ( n \right )=\left\{\begin{matrix} 0 & if\: n=1\\ T\left ( \frac{n}{2} \right )+1 & 否则 \ \ \end{矩阵}\right.$$

使用此递推关系T(n)=log n。

因此，二分查找使用O(log n)时间。

例子

在下面的实现中，我们尝试通过应用二元搜索算法从值列表中搜索整数值。

C C++ Java Python 
#include <stdio.h>
#define MAX 20

// array of items on which linear search will be conducted.
int intArray[MAX] = {1,2,3,4,6,7,9,11,12,14,15,16,17,19,33,34,43,45,55,66};
void printline(int count){
   int i;
   for(i = 0; i <count-1; i++) {
      printf("=");
   }
   printf("=\n");
}
int find(int data){
   int lowerBound = 0;
   int upperBound = MAX -1;
   int midPoint = -1;
   int comparisons = 0;
   int index = -1;
   while(lowerBound <= upperBound) {
      printf("Comparison %d\n" , (comparisons +1) );
      printf("lowerBound : %d, intArray[%d] = %d\n",lowerBound,lowerBound,
         intArray[lowerBound]);
      printf("upperBound : %d, intArray[%d] = %d\n",upperBound,upperBound,
         intArray[upperBound]);
      comparisons++;
      
      // compute the mid point
      // midPoint = (lowerBound + upperBound) / 2;
      midPoint = lowerBound + (upperBound - lowerBound) / 2;
      
      // data found
      if(intArray[midPoint] == data) {
         index = midPoint;
         break;
      } else {
         
         // if data is larger
         if(intArray[midPoint] < data) {
         
         // data is in upper half
            lowerBound = midPoint + 1;
         }
         
         // data is smaller
         else {
            
            // data is in lower half
            upperBound = midPoint -1;
         }
      }
   }
   printf("Total comparisons made: %d" , comparisons);
   return index;
}
void display(){
   int i;
   printf("[");
   
   // navigate through all items
   for(i = 0; i<MAX; i++) {
      printf("%d ",intArray[i]);
   }
   printf("]\n");
}
void main(){
   printf("Input Array: ");
   display();
   printline(50);
   
   //find location of 1
   int location = find(55);
   
   // if element was found
   if(location != -1)
      printf("\nElement found at location: %d" ,(location+1));
   else
      printf("\nElement not found.");
}

输出

Input Array: [1 2 3 4 6 7 9 11 12 14 15 16 17 19 33 34 43 45 55 66 ]
==================================================
Comparison 1
lowerBound : 0, intArray[0] = 1
upperBound : 19, intArray[19] = 66
Comparison 2
lowerBound : 10, intArray[10] = 15
upperBound : 19, intArray[19] = 66
Comparison 3
lowerBound : 15, intArray[15] = 34
upperBound : 19, intArray[19] = 66
Comparison 4
lowerBound : 18, intArray[18] = 55
upperBound : 19, intArray[19] = 66
Total comparisons made: 4
Element found at location: 19

#include<iostream>
using namespace std;
int binarySearch(int arr[], int p, int r, int num){
   if (p <= r) {
      int mid = (p + r)/2;
      if (arr[mid] == num)
         return mid ;
      if (arr[mid] > num)
         return binarySearch(arr, p, mid-1, num);
      if (arr[mid] < num)
         return binarySearch(arr, mid+1, r, num);
   }
   return -1;
}
int main(void){
   int arr[] = {1, 3, 7, 15, 18, 20, 25, 33, 36, 40};
   int n = sizeof(arr)/ sizeof(arr[0]);
   int num = 15;
   int index = binarySearch (arr, 0, n-1, num);
   if(index == -1) {
      cout<< num <<" is not present in the array";
   } else {
      cout<< num <<" is present at index "<< index <<" in the array";
   }
   return 0;
}

输出

15 is present at index 3 in the array

public class Binary_Search {
   public static int binarySearch(int arr[], int low, int high, int key) {
      int mid = (low + high)/2;
      while( low <= high ) {
         if ( arr[mid] < key ) {
            low = mid + 1;
         } else if ( arr[mid] == key ) {
            return mid;
         } else {
            high = mid - 1;
         }
         mid = (low + high)/2;
      }
      return -1;
   }
   public static void main(String args[]) {
      int[] arr = { 10, 20, 30, 40, 50, 60 };
      int key = 30;
      int high=arr.length-1;
      int i = binarySearch(arr,0,high,key);
      if (i != -1) {
         System.out.println(key + " is present at index: " + i);
      } else {
         System.out.println(key + " is not present.");
      }
   }
}

输出

30 is present at index: 2

def binarySearch(arr, low, high, key):
   mid = (low + high)//2
   while( low <= high ):
      if ( arr[mid] < key ):
         low = mid + 1
      elif ( arr[mid] == key ):
         return mid
      else:
         high = mid - 1
      mid = (low + high)//2
   return -1;

arr = [ 10, 20, 30, 40, 50, 60 ]
key = 50
high=len(arr)-1
i = binarySearch(arr,0,high,key)
if (i != -1):
   print("key is present at index: ")
   print(i)
else:
   print("key is not present.")

输出

key is present at index: 
4

施特拉森矩阵乘法

Strassen 的矩阵乘法是解决矩阵乘法问题的分而治之的方法。通常的矩阵乘法方法是将每一行与每一列相乘以获得乘积矩阵。这种方法的时间复杂度是O(n 3 )，因为它需要两个循环来进行乘法。引入 Strassen 方法将时间复杂度从O(n 3 )降低到O(n log 7 )。

朴素方法

首先，我们将讨论朴素方法及其复杂性。在这里，我们计算 Z=