离散数学-群论
半群
具有二元运算 $'\omicron'$ (组合)的有限或无限集合 $'S'$ 如果同时满足以下两个条件,则称为半群 -
闭包- 对于 S 中的每对 $(a, b) \, \:(a \omicron b)$ 必须出现在集合 $S$ 中。
关联性- 对于 S 中的每个元素 $a, b, c \in,(a \omicron b) \omicron c = a \omicron (b \omicron c)$ 必须成立。
例子
具有加法运算的正整数(不包括零)的集合是半群。例如,$ S = \lbrace 1, 2, 3, \dots \rbrace $
这里,对于每对 $(a, b) \in S,(a + b)$ 都存在于集合 S 中,闭包属性成立。例如, $1 + 2 = 3 \in S]$
关联属性也适用于 S 中的每个元素 $a, b, c,(a + b) + c = a + (b + c)$。例如,$(1 + 2) + 3 = 1 + (2 + 3) = 5$
幺半群
幺半群是具有单位元的半群。集合 S 的单位元素(用 $e$ 或 E 表示)是这样的元素:对于 S$ 中的每个元素 $a \omicron e) = a$。单位元也称为单位元。因此,幺半群同时拥有三个属性:闭包、关联、恒等元素。
例子
具有乘法运算的正整数(不包括零)的集合是幺半群。$S = \lbrace 1, 2, 3, \点 \rbrace $
这里闭包属性对于每对 $(a, b) \in S 来说都成立,(a \times b)$ 存在于集合 S 中。 [例如,$1 \times 2 = 2 \in S$ 等等]
关联属性也适用于 S 中的每个元素 $a, b, c \in S, (a \times b) \times c = a \times (b \times c)$ [例如,$(1 \times 2) \times 3 = 1 \times (2 \times 3) = 6$ 等等]
同一性属性也适用于 S 中的每个元素 $a \times e) = a$ [例如,$(2 \times 1) = 2, (3 \times 1) = 3$ 等等]。这里单位元为1。
团体
群是具有逆元素的幺半群。集合 S 的逆元素(用 I 表示)是这样的元素:对于 S$ 中的每个元素 $a \omicron I) = (I \omicron a) = a$。因此,一个群同时拥有四个属性 - i)闭包,ii)结合,iii)单位元素,iv)逆元素。群 G 的阶是 G 中元素的数量,群中元素的阶是最小正整数 n,使得 an 是该群 G 的单位元素。
例子
$N \times N$ 个非奇异矩阵的集合在矩阵乘法运算下形成一个群。
两个$N \times N$非奇异矩阵的乘积也是一个具有闭包性质的$N \times N$非奇异矩阵。
矩阵乘法本身是结合律的。因此,关联性质成立。
$N \times N$ 非奇异矩阵的集合包含具有单位元素属性的单位矩阵。
由于所有矩阵都是非奇异矩阵,因此它们都具有逆元素,这些元素也是非奇异矩阵。因此,逆性质也成立。
阿贝尔群
阿贝尔群 G 是元素对 $(a,b) \in G$ 始终满足交换律的群。因此,一个群同时拥有五个属性 - i) 闭包,ii) 结合性,iii) 单位元,iv) 逆元,v) 可交换。
例子
具有加法运算的正整数(包括零)的集合是阿贝尔群。$G = \lbrace 0, 1, 2, 3, \点 \rbrace$
这里,对于每对 $(a, b) \in S,(a + b)$ 都存在于集合 S 中,闭包属性成立。 [例如,$1 + 2 = 2 \in S$ 等等]
关联属性也适用于 S 中的每个元素 $a, b, c \in S, (a + b) + c = a + (b + c)$ [例如,$(1 +2) + 3 = 1 + (2 + 3) = 6$ 等等]
同一性属性也适用于 S 中的每个元素 $a \times e) = a$ [例如,$(2 \times 1) = 2, (3 \times 1) = 3$ 等等]。这里,单位元为1。
交换律也适用于 S 中的每个元素 $a \times b) = (b \times a)$ [例如,$(2 \times 3) = (3 \times 2) = 3$ 等等在]
循环群和子群
循环群是可以由单个元素生成的群。循环群的每个元素都是某个特定元素的幂,该元素称为生成元。循环群可以由生成器“g”生成,使得该群的每个其他元素都可以写成生成器“g”的幂。
例子
乘法运算下的复数集合 $\lbrace 1,-1, i, -i \rbrace$ 是一个循环群。
有两个生成器 - $i$ 和 $–i$ 作为 $i^1 = i, i^2 = -1, i^3 = -i, i^4 = 1$ 以及 $(–i)^1 = -i, (–i)^2 = -1, (–i)^3 = i, (–i)^4 = 1$ 覆盖了该组的所有元素。因此,它是一个循环群。
注-循环群始终是阿贝尔群,但并非每个阿贝尔群都是循环群。加法下的有理数不是循环的,而是阿贝尔的。
子群H 是群 G 的子集(用 $H ≤ G$ 表示),如果它同时满足四个属性 -闭包、关联、单位元和逆。
群G中不包含整个群G的子群H称为真子群(记为$H<G$)。循环群的子群是循环的,阿贝尔子群也是阿贝尔的。
例子
设一组 $G = \lbrace 1, i, -1, -i \rbrace$
那么一些子组是 $H_1 = \lbrace 1 \rbrace, H_2 = \lbrace 1,-1 \rbrace$,
这不是子群 − $H_3 = \lbrace 1, i \rbrace$ 因为 $(i)^{-1} = -i$ 不在 $H_3$ 中
偏序集 (POSET)
偏序集合由具有自反、反对称和传递的二元关系的集合组成。“偏序集”缩写为 POSET。
例子
二元运算下小于或等于$(\le)$的实数集合是偏序集。
设集合$S = \lbrace 1, 2, 3 \rbrace$,运算为$\le$
关系为 $\lbrace(1, 1), (2, 2), (3, 3), (1, 2), (1, 3), (2, 3)\rbrace$
该关系 R 自反为 $\lbrace (1, 1), (2, 2), (3, 3)\rbrace \in R$
该关系 R 是反对称的,如
$\lbrace (1, 2), (1, 3), (2, 3) \rbrace \in R\ 和\ \lbrace (1, 2), (1, 3), (2, 3) \rbrace ∉雷亚尔
该关系 R 也是传递性的,如 $\lbrace (1,2), (2,3), (1,3)\rbrace \in R$。
因此,它是一个偏序集。
有向无环图在“可达性”操作下的顶点集是偏序集。
哈斯图
偏序集的哈斯图是有向图,其顶点是偏序集的元素,弧覆盖偏序集中的对 (x, y)。如果在偏序集 $x < y$ 中,则点 x 在哈斯图中显得低于点 y。如果偏序集中 $x<y<z$,则 x 和 z 之间不会显示箭头,因为它是隐式的。
例子
$\lbrace 1, 2, 3 \rbrace = \lbrace \emptyset, \lbrace 1 \rbrace, \lbrace 2 \rbrace, \lbrace 3 \rbrace, \lbrace 1, 2 \rbrace, \lbrace 1 的子集偏序集, 3 \rbrace, \lbrace 2, 3 \rbrace, \lbrace 1, 2, 3 \rbrace \rbrace$ 由以下哈斯图显示 -
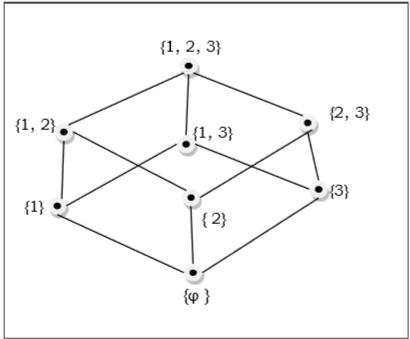
线性有序集
线性有序集或全序集是其中每对元素都是可比较的偏序集。如果 $a \le b$ 或 $b \le a$ 成立,则元素 $a, b \in S$ 被认为是可比较的。三分法定义了这个全有序集。全序集合可以定义为一个分配格,对于集合 S 中 a 和 b 的所有值,具有属性 $\lbrace a \lor b, a \land b \rbrace = \lbrace a, b \rbrace$ 。
例子
按 \subseteq 排序的 $\lbrace a, b \rbrace$ 的幂集是一个全序集,因为幂集 $P = \lbrace \emptyset, \lbrace a \rbrace, \lbrace b \rbrace, \ 的所有元素都是全序集。 lbrace a, b\rbrace \rbrace$ 是可比较的。
非总订单集示例
x 除 y 操作下的集合 $S = \lbrace 1, 2, 3, 4, 5, 6 \rbrace$ 不是全有序集。
这里,对于所有 $(x, y) \in S, x | y$ 必须成立,但 2 | 并不成立。3,因为2不能整除3或3不能整除2。因此,它不是全有序集。
格子
格是一个偏序集 $(L, \le)$,其中每对 $\lbrace a, b \rbrace \in L$ 都有一个最小上界(用 $a \lor b$ 表示)和一个最大下界(表示为$a \land b$)。LUB $(\lbrace a,b \rbrace)$ 称为 a 和 b 的连接。GLB $(\lbrace a,b \rbrace )$ 称为 a 和 b 的交集。
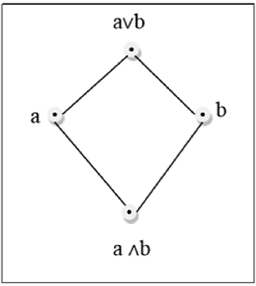
例子
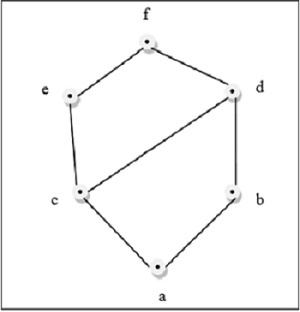
上图是一个格,因为对于 L$ 中的每对 $\lbrace a, b \rbrace \,都存在一个 GLB 和一个 LUB。
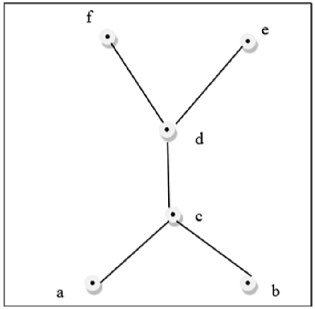
上图不是格子,因为 $GLB (a, b)$ 和 $LUB (e, f)$ 不存在。
下面讨论一些其他格子 -
有界格子
如果格子 L 具有最大元素 1 和最小元素 0,则该格子 L 成为有界格子。
补格
如果格子 L 是有界格子并且格子中的每个元素都有补集,则它成为补格子。如果 $\exists x(x \land x'=0 and x \lor x' = 1)$,则元素 x 具有补集 x'
分配格
如果一个格满足以下两个分布性质,则称为分布格。
$a \lor (b \land c) = (a \lor b) \land (a \lor c)$
$a \land (b \lor c) = (a \land b) \lor (a \land c)$
模块化格子
如果一个格满足以下性质,则称为模格。
$a \land( b \lor (a \land d)) = (a \land b) \lor (a \land d)$
格子的性质
幂等属性
$a \或a = a$
$a \land a = a$
吸收特性
$a \lor (a \land b) = a$
$a \land (a \lor b) = a$
交换性质
$a \lor b = b \lor a$
$a \land b = b \land a$
关联属性
$a \lor (b \lor c) = (a \lor b) \lor c$
$a \land (b \land c) = (a \land b) \land c$
格子的对偶
格的对偶是通过交换“$\lor$”和“$\land$”运算获得的。
例子
$\lbrack a \lor (b \land c) \rbrack\ 的对偶是\ \lbrack a \land (b \lor c) \rbrack$
