离散数学 - 关系
每当讨论集合时,接下来就会出现集合元素之间的关系。关系可以存在于同一集合的对象之间或者两个或多个集合的对象之间。
定义和属性
从集合 x 到 y 的二元关系 R(写为 $xRy$ 或 $R(x,y)$)是笛卡尔积 $x \times y$ 的子集。如果 G 的有序对颠倒,关系也会改变。
通常,集合 $A_1、\dots 、\ 和\ A_n$ 之间的 n 元关系 R 是 n 元乘积 $A_1 \times \dots \times A_n$ 的子集。在这种情况下,关系 R 的最小基数为零,最大基数为 $n^2$。
单个集合 A 上的二元关系 R 是 $A \times A$ 的子集。
对于两个不同的集合 A 和 B,分别具有基数m和n,从 A 到 B 的关系 R 的最大基数是mn。
域和范围
如果有两个集合 A 和 B,且关系 R 具有阶对 (x, y),则 -
R 的定义域Dom(R) 是集合 $\lbrace x \:| \: (x, y) \in R \:对于某些\: y\: in\: B \rbrace$
R 的范围Ran(R) 是集合 $\lbrace y\: |\: (x, y) \in R \:for\: some\: x\: in\: A\rbrace $
例子
让 $A = \lbrace 1, 2, 9 \rbrace $ 和 $ B = \lbrace 1, 3, 7 \rbrace$
情况 1 - 如果关系 R “等于”,则 $R = \lbrace (1, 1), (3, 3) \rbrace$
Dom(R) = $\lbrace 1, 3 \rbrace , Ran(R) = \lbrace 1, 3 \rbrace$
情况 2 - 如果关系 R 为“小于”,则 $R = \lbrace (1, 3), (1, 7), (2, 3), (2, 7) \rbrace$
Dom(R) = $\lbrace 1, 2 \rbrace , Ran(R) = \lbrace 3, 7 \rbrace$
情况 3 - 如果关系 R “大于”,则 $R = \lbrace (2, 1), (9, 1), (9, 3), (9, 7) \rbrace$
Dom(R) = $\lbrace 2, 9 \rbrace , Ran(R) = \lbrace 1, 3, 7 \rbrace$
使用图表示关系
关系可以使用有向图来表示。
图中的顶点数等于定义关系的集合中的元素数。对于关系 R 中的每个有序对 (x, y),都会有一条从顶点“x”到顶点“y”的有向边。如果存在有序对(x,x),则顶点x上将存在自环。
假设,集合 $S = \lbrace 1, 2, 3 \rbrace$ 上存在关系 $R = \lbrace (1, 1), (1,2), (3, 2) \rbrace$,则可以为由下图表示 -
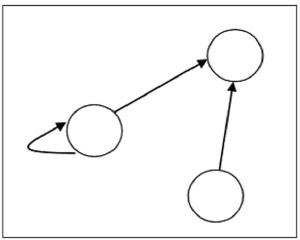
关系类型
集合 X 和 Y 之间或 E 上的空关系是空集合 $\emptyset$
集合 X 和 Y 之间的完整关系是集合 $X \times Y$
集合 X 上的恒等关系是集合 $\lbrace (x, x) | x \in X \rbrace$
关系 R 的逆关系 R' 定义为 − $R' = \lbrace (b, a) | (a, b) \in R \rbrace$
示例- 如果 $R = \lbrace (1, 2), (2, 3) \rbrace$ 则 $R' $ 将是 $\lbrace (2, 1), (3, 2) \rbrace$
如果 $\forall a \in A$ 与 a 相关(aRa 成立),则集合A 上的关系 R 称为自反关系
示例- 集合 $X = \lbrace a, b \rbrace$ 上的关系 $R = \lbrace (a, a), (b, b) \rbrace$ 是自反的。
如果 A$ 中没有 $a \in A$ 与 a 相关(aRa 不成立),则集合 A上的关系 R 称为Irreflexive 。
示例- 集合 $X = \lbrace a, b \rbrace$ 上的关系 $R = \lbrace (a, b), (b, a) \rbrace$ 是反反的。
如果 $xRy$ 暗示 $yRx$、$\forall x \in A$ 和 $\forall y \in A$ ,则集合 A 上的关系 R 称为对称关系。
示例- 集合 $A = \lbrace 1, 2, 3 \rbrace$ 上的关系 $R = \lbrace (1, 2), (2, 1), (3, 2), (2, 3) \rbrace$是对称的。
如果 $xRy$ 和 $yRx$ 意味着 $x = y \: \forall x \in A$ 和 $\forall y \in A$,则集合 A 上的关系 R 称为反对称关系。
示例- 关系 $R = \lbrace (x, y)\to N |\:x \leq y \rbrace$ 是反对称的,因为 $x \leq y$ 和 $y \leq x$ 意味着 $x = y $。
如果 $xRy$ 和 $yRz$ 暗示 $xRz,\forall x,y,z \in A$,则集合 A上的关系 R 称为传递性的。
示例- 集合 $A = \lbrace 1, 2, 3 \rbrace$ 上的关系 $R = \lbrace (1, 2), (2, 3), (1, 3) \rbrace$ 是传递的。
如果关系是自反、对称和传递的,则该关系是等价关系。
示例- 关系 $R = \lbrace (1, 1), (2, 2), (3, 3), (1, 2), (2,1), (2,3), (3,2) , (1,3), (3,1) \rbrace$ 在集合 $A = \lbrace 1, 2, 3 \rbrace$ 上是一个等价关系,因为它是自反、对称和传递的。
