离散数学 - 集合
德国数学家G.康托尔提出了集合的概念。他将集合定义为通过某些规则或描述选择的明确且可区分的对象的集合。
集合论构成了其他几个研究领域的基础,例如计数理论、关系、图论和有限状态机。在本章中,我们将介绍集合论的不同方面。
集合 - 定义
集合是不同元素的无序集合。可以通过使用集合括号列出其元素来显式地编写集合。如果元素的顺序发生更改或集合中的任何元素重复,则不会对集合进行任何更改。
集合的一些例子
- 所有正整数的集合
- 太阳系中所有行星的集合
- 印度所有州的集合
- 字母表中所有小写字母的集合
集合的表示
集合可以用两种方式表示 -
- 名册或表格形式
- 集合生成器符号
名册或表格形式
该集合通过列出组成它的所有元素来表示。元素括在大括号内并用逗号分隔。
示例 1 - 英语字母表中的元音集,$A = \lbrace a,e,i,o,u \rbrace$
示例 2 - 小于 10 的奇数集,$B = \lbrace 1,3,5,7,9 \rbrace$
集合生成器符号
该集合是通过指定该集合的元素所共有的属性来定义的。该集合被描述为 $A = \lbrace x : p(x) \rbrace$
示例 1 - 集合 $\lbrace a,e,i,o,u \rbrace$ 写为 -
$A = \lbrace x : \text{x 是英文字母中的元音} \rbrace$
示例 2 - 集合 $\lbrace 1,3,5,7,9 \rbrace$ 写为 -
$B = \lbrace x : 1 \le x \lt 10 \ and\ (x \% 2) \ne 0 \rbrace$
如果元素 x 是任意集合 S 的成员,则用 $x \in S$ 表示,如果元素 y 不是集合 S 的成员,则用 $y \notin S$ 表示。
示例-如果 $S = \lbrace1, 1.2, 1.7, 2\rbrace , 1 \in S$ 但 $1.5 \notin S$
一些重要的集合
N − 所有自然数的集合 = $\lbrace1, 2, 3, 4, .....\rbrace$
Z − 所有整数的集合 = $\lbrace....., -3, -2, -1, 0, 1, 2, 3, .....\rbrace$
Z + − 所有正整数的集合
Q - 所有有理数的集合
R - 所有实数的集合
W - 所有整数的集合
集合的基数
集合 S 的基数,用 $|S|$ 表示,是集合中元素的数量。该数字也称为基数。如果一个集合有无限个元素,它的基数是$\infty$。
示例- $|\lbrace 1, 4, 3, 5 \rbrace | = 4, | \lbrace 1, 2, 3, 4, 5, \点 \rbrace | = \infty$
如果有两个集合X和Y,
$|X| = |Y|$ 表示具有相同基数的两个集合 X 和 Y。当 X 中的元素数量恰好等于 Y 中的元素数量时,就会发生这种情况。在这种情况下,存在从 X 到 Y 的双射函数“f”。
$|X| \le |Y|$ 表示集合 X 的基数小于或等于集合 Y 的基数。当 X 中的元素数量小于或等于 Y 中的元素数量时,就会发生这种情况。这里,存在从 X 到 Y 的单射函数“f”。
$|X| \lt |Y|$ 表示集合 X 的基数小于集合 Y 的基数。当 X 中的元素数量小于 Y 中的元素数量时,就会发生这种情况。这里,从 X 到 Y 的函数“f”是单射函数,但不是双射函数。
$如果\ |X| \le |Y|$ 和 $|X| \ge |Y|$ 然后 $|X| = |Y|$。集合 X 和 Y 通常称为等价集合。
套装类型
集合可以分为多种类型。其中一些是有限集、无限集、子集、全集、真集、单例集等。
有限集
包含一定数量元素的集合称为有限集合。
示例- $S = \lbrace x \:| \:x \in N$ 和 $70 \gt x \gt 50 \rbrace$
无限集
包含无限个元素的集合称为无限集。
示例- $S = \lbrace x \: | \: x \in N $ 和 $ x \gt 10 \rbrace$
子集
如果 X 的每个元素都是集合 Y 的元素,则集合 X 是集合 Y 的子集(写为 $X \subseteq Y$)。
示例 1 - 让 $X = \lbrace 1, 2, 3, 4, 5, 6 \rbrace$ 和 $Y = \lbrace 1, 2 \rbrace$。这里集合Y是集合X的子集,因为集合Y的所有元素都在集合X中。因此,我们可以写$Y \subseteq X$。
示例 2 - 让 $X = \lbrace 1, 2, 3 \rbrace$ 和 $Y = \lbrace 1, 2, 3 \rbrace$。这里集合 Y 是集合 X 的子集(不是真子集),因为集合 Y 的所有元素都在集合 X 中。因此,我们可以写 $Y \subseteq X$。
真子集
术语“真子集”可以定义为“但不等于”的子集。如果 X 的每个元素都是集合 Y 的元素且 $|X| ,则集合 X 是集合 Y 的真子集(写为 $ X \subset Y $)\lt |Y|$。
示例- 设 $X = \lbrace 1, 2, 3, 4, 5, 6 \rbrace$ 和 $Y = \lbrace 1, 2 \rbrace$。这里设置$Y \subset X$,因为$Y$中的所有元素也包含在$X$中,并且$X$至少有一个元素比集合$Y$多。
通用套装
它是特定上下文或应用程序中所有元素的集合。该上下文或应用程序中的所有集合本质上都是该通用集合的子集。通用集表示为 $U$。
示例- 我们可以将 $U$ 定义为地球上所有动物的集合。在这种情况下,所有哺乳动物的集合是 $U$ 的子集,所有鱼类的集合是 $U$ 的子集,所有昆虫的集合是 $U$ 的子集,依此类推。
空集或零集
空集不包含任何元素。它用$\emptyset$ 表示。由于空集的元素个数是有限的,所以空集是有限集。空集或空集的基数为零。
示例- $S = \lbrace x \:| \: x \in N$ 和 $7 \lt x \lt 8 \rbrace = \emptyset$
单例集或单元集
单例集或单元集仅包含一个元素。单例集用 $\lbrace s \rbrace$ 表示。
示例- $S = \lbrace x \:| \:x \in N,\ 7 \lt x \lt 9 \rbrace$ = $\lbrace 8 \rbrace$
等集
如果两个集合包含相同的元素,则称它们相等。
示例- 如果 $A = \lbrace 1, 2, 6 \rbrace$ 和 $B = \lbrace 6, 1, 2 \rbrace$,则它们相等,因为集合 A 的每个元素都是集合 B 的元素,并且集合 A 的每个元素都是集合 B 的元素集合B是集合A的元素。
等效组
如果两个集合的基数相同,则称它们为等价集合。
示例- 如果 $A = \lbrace 1, 2, 6 \rbrace$ 和 $B = \lbrace 16, 17, 22 \rbrace$,它们是等效的,因为 A 的基数等于 B 的基数。即 $|A | =|B| = 3$
重叠集
至少有一个公共元素的两个集合称为重叠集合。
如果集合重叠 -
$n(A \cup B) = n(A) + n(B) - n(A \cap B)$
$n(A \cup B) = n(A - B) + n(B - A) + n(A \cap B)$
$n(A) = n(A - B) + n(A \cap B)$
$n(B) = n(B - A) + n(A \cap B)$
示例- 设 $A = \lbrace 1, 2, 6 \rbrace$ 和 $B = \lbrace 6, 12, 42 \rbrace$。有一个公共元素“6”,因此这些集合是重叠集合。
不相交集
如果两个集合 A 和 B 甚至没有一个共同元素,则这两个集合称为不相交集合。因此,不相交集具有以下属性 -
$n(A \cap B) = \emptyset$
$n(A \杯子 B) = n(A) + n(B)$
示例- 假设 $A = \lbrace 1, 2, 6 \rbrace$ 和 $B = \lbrace 7, 9, 14 \rbrace$,没有单个公共元素,因此这些集合是重叠集合。
维恩图
维恩图,由约翰·维恩于1880年发明,是一种显示不同数学集合之间所有可能的逻辑关系的示意图。
例子
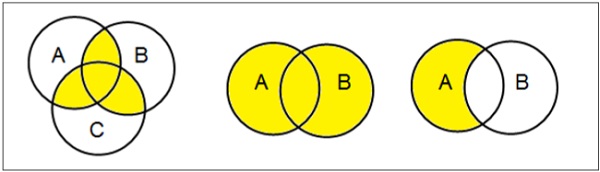
设置操作
集合运算包括集合并、集合交、集合差、集合补和笛卡尔积。
集合联盟
集合 A 和 B 的并集(表示为 $A \cup B$)是 A 中、B 中或 A 和 B 中的元素的集合。因此,$A \cup B = \lbrace x \: | \: x \in A\ OR\ x \in B \rbrace$。
示例- 如果 $A = \lbrace 10, 11, 12, 13 \rbrace$ 且 B = $\lbrace 13, 14, 15 \rbrace$,则 $A \cup B = \lbrace 10, 11, 12, 13, 14, 15 \rbrace$。(公共元素只出现一次)
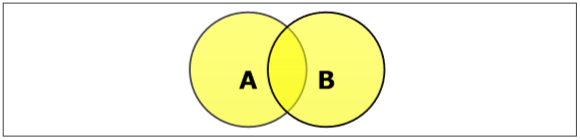
设置交集
集合 A 和 B 的交集(记为 $A \cap B$)是同时位于 A 和 B 中的元素的集合。因此,$A \cap B = \lbrace x \:|\: x \in A \ AND\ x \in B \rbrace$。
示例- 如果 $A = \lbrace 11, 12, 13 \rbrace$ 且 $B = \lbrace 13, 14, 15 \rbrace$,则 $A \cap B = \lbrace 13 \rbrace$。
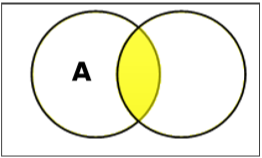
设置差异/相对补集
集合 A 和 B 的集合差(记为 $A – B$)是只在 A 中而不在 B 中的元素的集合。因此,$A - B = \lbrace x \:| \: x \in A\ AND\ x \not B \rbrace$。
示例- 如果 $A = \lbrace 10, 11, 12, 13 \rbrace$ 且 $B = \lbrace 13, 14, 15 \rbrace$,则 $(A - B) = \lbrace 10, 11, 12 \rbrace $ 和 $(B - A) = \lbrace 14, 15 \rbrace$。在这里,我们可以看到 $(A - B) \ne (B - A)$
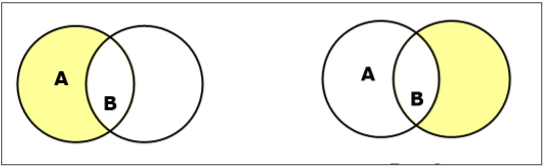
集合的补集
集合 A 的补集(用 $A'$ 表示)是不在集合 A 中的元素的集合。因此,$A' = \lbrace x | x \notin A \rbrace$。
更具体地说,$A'= (U - A)$,其中$U$ 是包含所有对象的通用集。
示例- 如果 $A = \lbrace x \:| \: x\ \: {属于奇数整数的集合} \rbrace$ 则 $A' = \lbrace y\: | \: y\ \: {不属于\: 奇数整数的集合} \rbrace$
笛卡尔积/叉积
n 个集合 $A_1, A_2, \dots A_n$ 的笛卡尔积表示为 $A_1 \times A_2 \dots \times A_n$ 可以定义为所有可能的有序对 $(x_1, x_2, \dots x_n)$ 其中$x_1 \在 A_1 中,x_2 \在 A_2 中,\点 x_n \在 A_n$ 中
示例- 如果我们采用两个集合 $A = \lbrace a, b \rbrace$ 和 $B = \lbrace 1, 2 \rbrace$,
A 和 B 的笛卡尔积写为 − $A \times B = \lbrace (a, 1), (a, 2), (b, 1), (b, 2)\rbrace$
B 和 A 的笛卡尔积写为 − $B \times A = \lbrace (1, a), (1, b), (2, a), (2, b)\rbrace$
电源组
集合S的幂集是S的所有子集(包括空集)的集合。基数为 n 的集合 S 的幂集的基数为 $2^n$。幂集表示为$P(S)$。
示例 -
对于集合 $S = \lbrace a, b, c, d \rbrace$ 让我们计算子集 -
具有 0 个元素的子集 - $\lbrace \emptyset \rbrace$ (空集)
具有 1 个元素的子集 - $\lbrace a \rbrace、\lbrace b \rbrace、\lbrace c \rbrace、\lbrace d \rbrace$
具有 2 个元素的子集 - $\lbrace a, b \rbrace, \lbrace a,c \rbrace, \lbrace a, d \rbrace, \lbrace b, c \rbrace, \lbrace b,d \rbrace,\lbrace c, d \r大括号$
具有 3 个元素的子集 - $\lbrace a ,b, c\rbrace,\lbrace a, b, d \rbrace, \lbrace a,c,d \rbrace,\lbrace b,c,d \rbrace$
具有 4 个元素的子集 - $\lbrace a, b, c, d \rbrace$
因此,$P(S)=$
$\lbrace \quad \lbrace \emptyset \rbrace、\lbrace a \rbrace、\lbrace b \rbrace、\lbrace c \rbrace、\lbrace d \rbrace、\lbrace a,b \rbrace、\lbrace a,c \ rbrace, \lbrace a,d \rbrace, \lbrace b,c \rbrace, \lbrace b,d \rbrace, \lbrace c,d \rbrace, \lbrace a,b,c \rbrace, \lbrace a,b, d \rbrace, \lbrace a,c,d \rbrace, \lbrace b,c,d \rbrace, \lbrace a,b,c,d \rbrace \quad \rbrace$
$| P(S)| = 2^4 = 16$
注意- 空集的幂集也是空集。
$| P (\lbrace \emptyset \rbrace) | P (\lbrace \emptyset \rbrace) | = 2^0 = 1$
集合的划分
一个集合的划分,比如S ,是n 个不相交子集的集合,比如 $P_1, P_2, \dots P_n$ 满足以下三个条件 -
$P_i$ 不包含空集。
$\lbrack P_i \ne \lbrace \emptyset \rbrace\ for\ all\ 0 \lt i \le n \rbrack$
子集的并集必须等于整个原始集。
$\lbrack P_1 \cup P_2 \cup \dots \cup P_n = S \rbrack$
任何两个不同集合的交集都是空的。
$\lbrack P_a \cap P_b = \lbrace \emptyset \rbrace,\ for\ a \ne b\ 其中\ n \ge a,\: b \ge 0 \rbrack$
例子
设 $S = \lbrace a, b, c, d, e, f, g, h \rbrace$
一种可能的分区是 $\lbrace a \rbrace, \lbrace b, c, d \rbrace, \lbrace e, f, g, h \rbrace$
另一个可能的分区是 $\lbrace a, b \rbrace, \lbrace c, d \rbrace, \lbrace e, f, g, h \rbrace$
铃声号码
贝尔数给出了划分集合的方法的数量。它们用 $B_n$ 表示,其中 n 是集合的基数。
示例-
设 $S = \lbrace 1, 2, 3\rbrace$, $n = |S| = 3$
备用分区是 -
1. $\emptyset , \lbrace 1, 2, 3 \rbrace$
2. $\lbrace 1 \rbrace , \lbrace 2, 3 \rbrace$
3. $\lbrace 1, 2 \rbrace , \lbrace 3 \rbrace$
4. $\lbrace 1, 3 \rbrace , \lbrace 2 \rbrace$
5. $\lbrace 1 \rbrace , \lbrace 2 \rbrace , \lbrace 3 \rbrace$
因此 $B_3 = 5$
