雷达系统 - 概述

雷达是一种基于电磁的探测系统，其工作原理是辐射电磁波，然后研究回波或反射回波。

雷达的完整形式是无线电检测和测距。 _ 检测是指目标是否存在。目标可以是静止的或可移动的，即非静止的。测距是指雷达与目标之间的距离。

雷达可用于地面、海上和太空的各种应用。下面列出了雷达的应用。

在雷达的任何应用中，基本原理都是相同的。现在我们来讨论一下雷达的原理。

雷达基本原理

雷达用于检测物体并找到它们的位置。我们可以从下图了解雷达的基本原理。

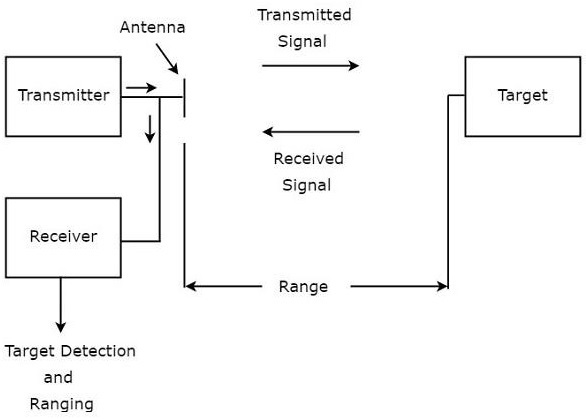
如图所示，雷达主要由发射机和接收机组成。它使用相同的天线来发送和接收信号。发射器的功能是向存在目标的方向发射雷达信号。

目标在各个方向反射接收到的信号。反射回天线的信号被接收器接收。

以下是本教程中有用的基本术语。

现在，让我们一一讨论这些基本术语。

雷达与目标之间的距离称为目标的射程或简称距离R。我们知道雷达向目标发射信号，目标则以光速向雷达发送回波信号C。

令信号从雷达传播到目标并返回雷达所需的时间为“T”。雷达和目标之间的双向距离将为 2R，因为雷达和目标之间的距离为 R。

现在，以下是Speed的公式。

$$速度= \frac{距离}{时间}$$

$$\Rightarrow 距离=速度\次时间$$

$$\右箭头 2R=C\times T$$

$$R=\frac{CT}{2}\:\:\:\:\:方程\:1$$

我们可以通过将 C 和 T 的值代入等式 1 来找到目标的范围。

雷达信号应在每个时钟脉冲传输。应适当选择两个时钟脉冲之间的持续时间，使得应在下一个时钟脉冲之前接收到与当前时钟脉冲相对应的回波信号。典型的雷达波形如下图所示。

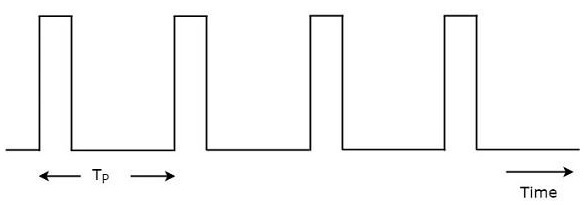
如图所示，雷达发射周期信号。它具有一系列狭窄的矩形脉冲。连续时钟脉冲之间的时间间隔称为脉冲重复时间$T_P$。

脉冲重复时间的倒数称为脉冲重复频率，$f_P$。在数学上，它可以表示为

$$f_P=\frac{1}{T_P}\:\:\:\:\:方程\:2$$

因此，脉冲重复频率只不过是雷达发射信号的频率。

我们知道雷达信号应该在每个时钟脉冲传输。如果我们选择两个时钟脉冲之间较短的持续时间，则将在下一个时钟脉冲之后接收到当前时钟脉冲对应的回波信号。因此，目标的射程似乎比实际射程要小。

因此，我们必须选择两个时钟脉冲之间的持续时间，以便在下一个时钟脉冲开始之前接收到当前时钟脉冲对应的回波信号。然后，我们就得到了目标的真实距离，也称为目标的最大无模糊距离，或者简称为最大无模糊距离。

将 $R=R_{un}$ 和 $T=T_P$ 代入公式 1。

$$R_{un}=\frac{CT_P}{2}\:\:\:\:\:方程\:3$$

从公式 2 中，我们将得到脉冲重复时间 $T_P$，它是脉冲重复频率 $f_P$ 的倒数。在数学上，它可以表示为

$$T_P=\frac{1}{f_P}\:\:\:\:\:方程\:4$$

将公式 4 代入公式 3。

$$R_{un}=\frac{C\left ( \frac{1}{f_P} \right )}{2}$$

$$R_{un}=\frac{C}{2f_P}\:\:\:\:\:方程\:5$$

我们可以使用公式 3 或公式 5 来计算目标的最大无模糊范围。

当我们考虑从雷达发射信号后到雷达接收到回波信号所需的时间作为脉冲宽度时，我们将得到目标的最小范围。也称为目标的最短射程。

将 $R=R_{min}$ 和 $T=\tau$ 代入方程 1。

$$R_{min}=\frac{C\tau}{2}\:\:\:\:\:方程\:6$$

将 $C$ 和 $\tau$ 的值代入公式 6 中，即可得到目标的最小范围值 $R_{min}$。